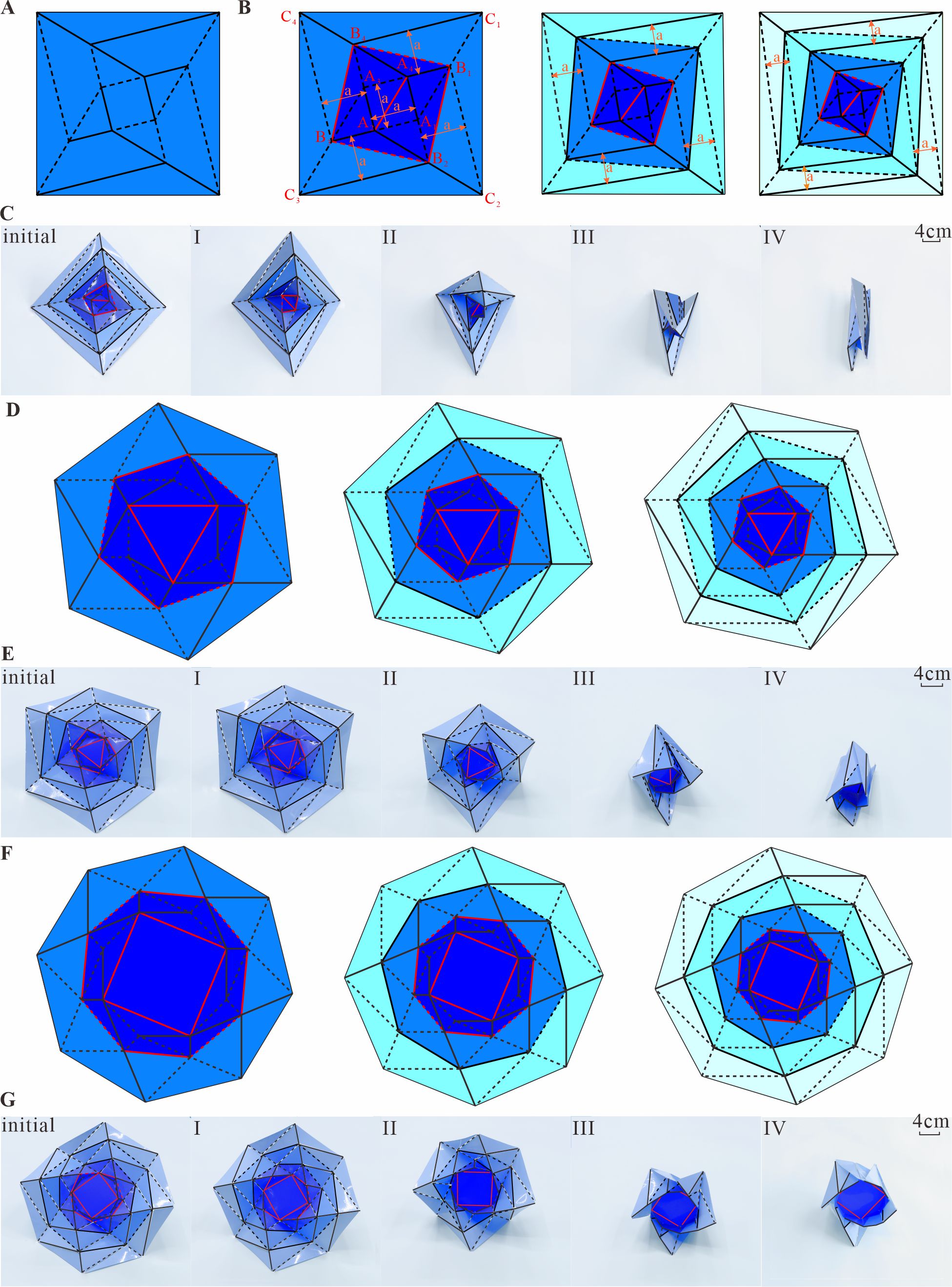
导读

        近日，天津大学陈焱教授和马家耀教授团队提出了一系列具有多稳态特性的可扩展折纸结构，通过机构运动学分析揭示了该折纸结构从内向外的逐层延迟折叠特性对其多稳态产生的关键作用，并通过力学分析探究了该结构基于材料与几何参数的可编程多稳态特性。相关研究成果以“Multi-Stability of the Extensible Origami Structures”为题于2023年8月8日在线发表在国际权威期刊《Advanced Science》上。论文的共同通讯作者为天津大学陈焱教授和马家耀教授，共同第一作者为天津大学博士生袭凯莉与博士生柴思博。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

研究背景

        双稳态与多稳态结构可以在两种或多种稳定构型之间快速切换，从而具有多种几何结构和不同的力学性能，已广泛应用于可重构机器人、执行器、MEMS、机械逻辑、机械存储器、机械信号传播等工程领域。非刚性折纸通常具有初始展平态与目标折叠状态这两个零能量状态，例如原始的缠绕折纸结构可以从展平态折叠到紧密缠绕在中心轮毂周围的状态，且其仅在展平态和紧密缠绕状态是几何协调的。这种独特的特性使它们十分适合用于构造双稳态结构。然而在构建多稳态结构时，现有研究往往只能通过将多个双稳态单元组合来实现，从而形成一维串联、二维阵列以及三维空间的结构形式。很少有独立的折纸单元具有多个稳定状态，而少数的多稳态折纸单元又往往通过运动分岔来实现，这就加大了在分岔点的控制难度，同时其稳态数量也很难通过折纸图案的扩展来进一步增加。

研究亮点

        针对上述问题，通过对图1A中的原始缠绕折纸图案添加折痕，并对其进行径向扩展，研究人员设计了一系列具有多稳态特性的四边形、六边形和八边形多层可扩展的折纸结构。该折纸结构的折叠过程如图1与视频1所示，具有旋转对称性的各层面板从内向外依次缠绕在中心多边形轮毂的周围，且除中心层（红色方框包围区域）外的每一层结构在达到紧密缠绕的状态时均可以稳定存在，也就是说每向外扩展一层都会增加一个额外的稳定状态。

图1 四边形、六边形和八边形可扩展缠绕折纸的折痕图案和物理模型

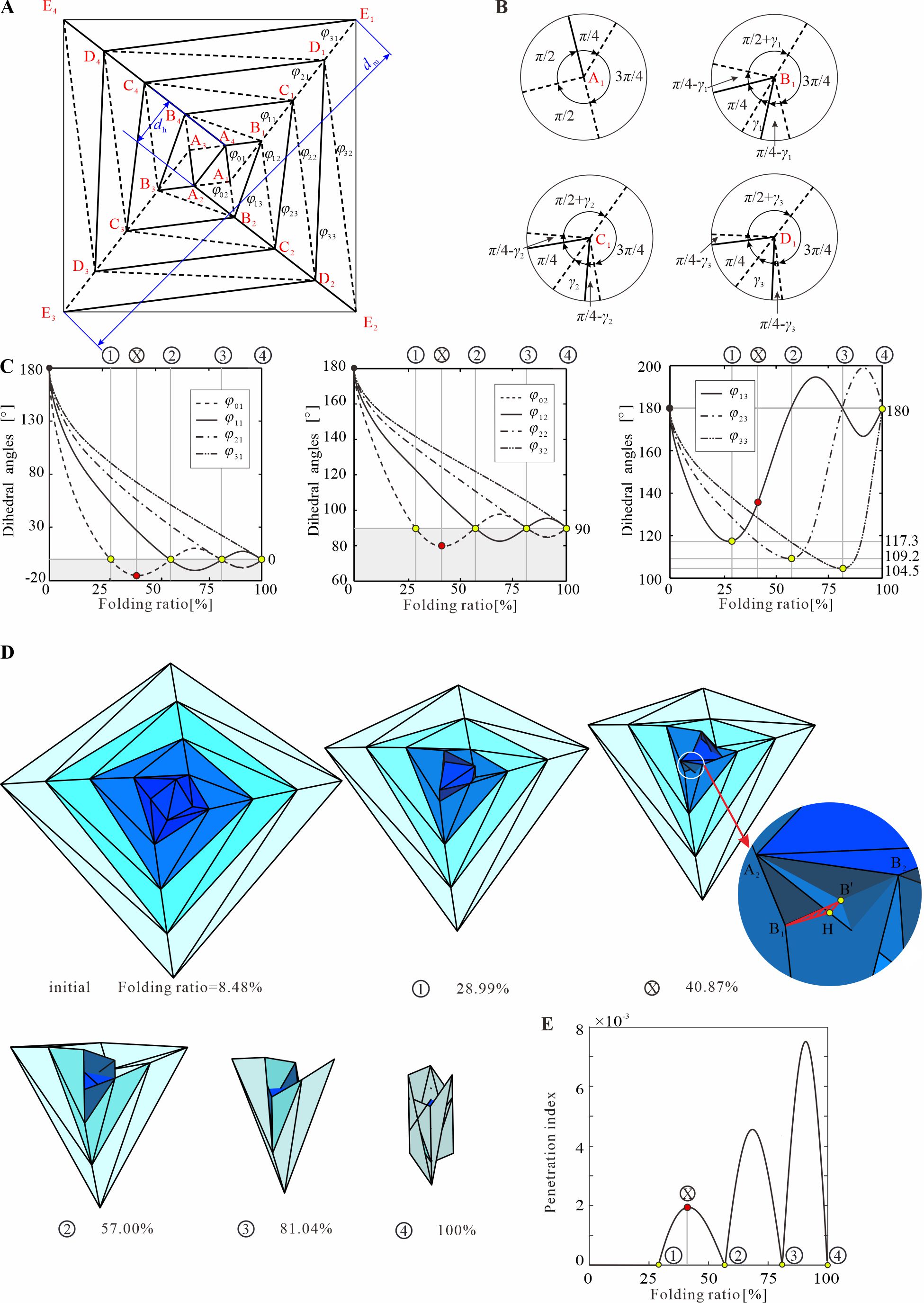
视频 1

        为了探究可扩展缠绕折纸的折叠行为与多稳态特性，研究人员首先以四层四边形缠绕折纸结构为例，利用Truss方法对其进行了运动学分析。如图2中的运动学曲线所示，该结构不同层之间的折叠行为具有高度的相似性，且其相同位置的二面角之间存在明显的相位延迟。这种延迟折叠特性带来了一个刚性折纸区间和几个离散的刚性折纸状态点。这些状态点被几个由面板穿透产生的非刚性折纸区间分隔开，且状态点的数量是由扩展的层数决定的。

图2 四层四边形缠绕折纸的运动学分析

        进一步地，研究人员通过实验和数值仿真研究了可扩展多稳态折纸结构的力学特性。如图3与视频2所示，该折纸结构在单轴拉伸加载下，其力-位移曲线体现出了典型的多稳态特性，且局部峰值力逐层增加。在消除折痕刚度的影响后，结构的稳定状态点与运动学得到的刚性折纸状态点十分吻合，从而证明了延迟折叠的运动学行为对其多稳态的产生具有关键作用。此外，研究发现面板与折痕的刚度比越大，折痕扭转越明显，局部峰值力越高；而当面板与折痕的刚度比较小时，结构的变形模式将发生转变，面板形成移动铰链，局部峰值力降低。

图3 四边形缠绕折纸结构的变形与稳态特性

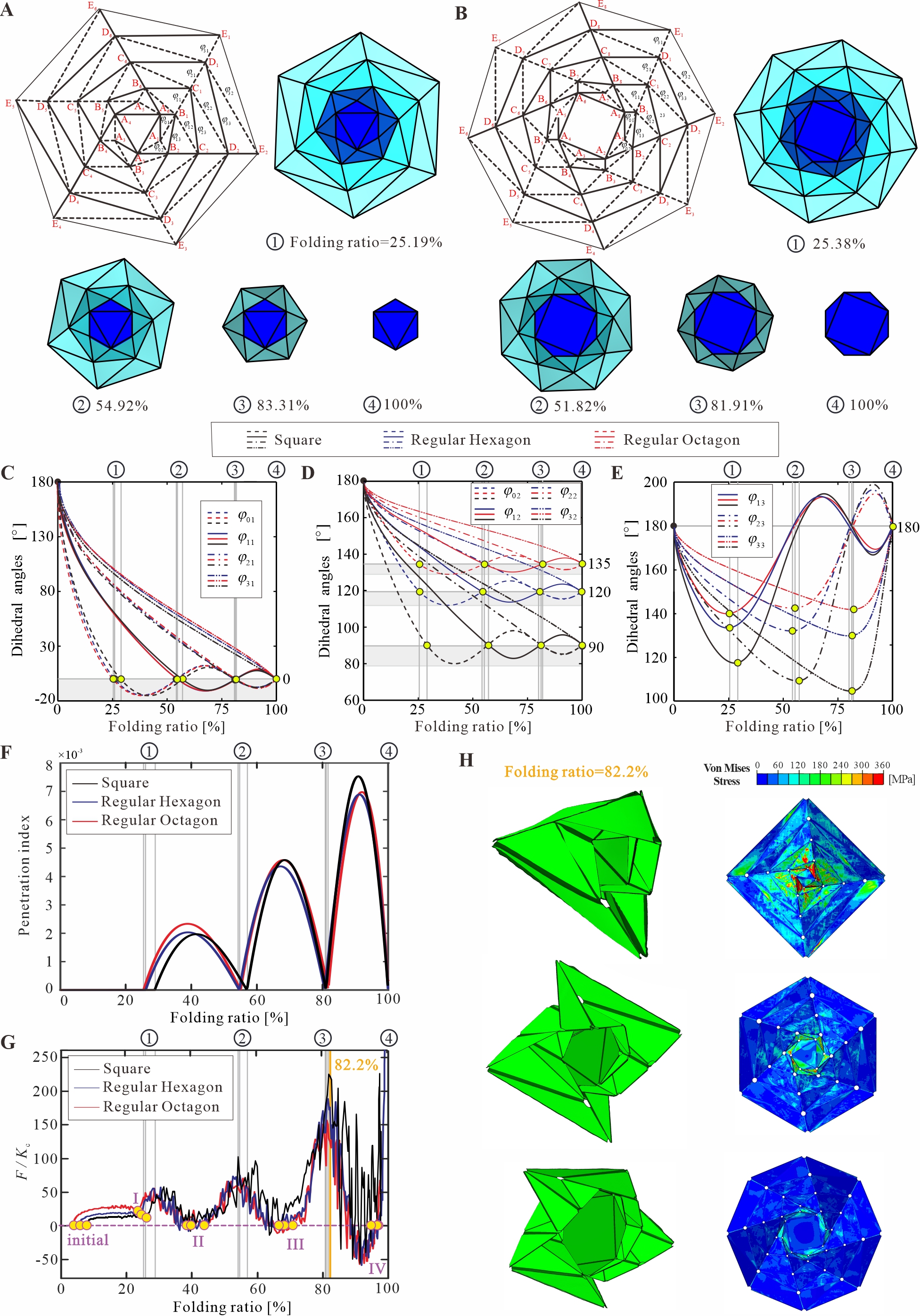
视频 2

        这种可扩展的多稳态特性并不是四边形折纸结构所独有的，研究人员进一步探究了四层的六边形与八边形可扩展折纸结构的稳态特性，并将其与四边形对应的结构进行了对比。研究发现，增加中心轮毂的边数对局部峰值力影响不大，但可以降低结构整体的最大应力，以实现更均匀的应力分布，从而避免或减轻折叠过程中的材料失效。

图4 不同轮毂形状的可扩展缠绕折纸结构的多稳态特性

总结与展望

        综上所述，本研究设计了一系列可扩展的具有多稳态特性的四边形、六边形和八边形缠绕折纸结构，且该结构可以通过镶嵌的方式构建具有更大体折展比的多稳态结构。文中所展示的缠绕折纸结构仅扩展到四层，实际上仍可以扩展到更多层以获取更多数量的稳定状态。未来，研究人员将运用文中的设计原理，结合其他非刚性折纸图案来构建更多的多稳态结构。该研究提供了一种独特而有效的多稳态结构的设计方法，有望应用于更多的工程领域，如软体机器人、机械计算和多功能超材料等。

Xi K#, Chai S#, Ma J*, Chen Y*. Multi-Stability of the Extensible Origami Structures. Advanced Science, 2023, 2303454.
(https://doi.org/10.1002/advs.202303454)