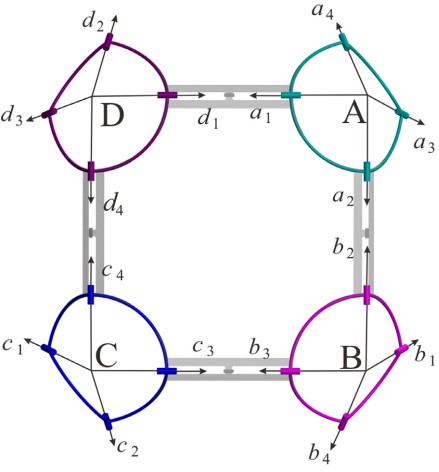
折纸是一门通过将平面纸张变成三维空间结构的艺术，而刚性折纸是一种特殊折纸类型，在其折叠过程中构成折纸图案的平面单元不会发生塑性变形，因此其折痕和平面单元可分别视为铰链和杆件。由四条折痕汇于一点构成的单顶点折纸可视为球面四杆机构，而四折痕顶点构成的刚性折纸图案可被视为由球面四杆机构构成的装配体，因此可以根据球面四杆机构的运动学原理对四折痕顶点构成的刚性折纸图案进行分析和设计，但是，用上述方法分析刚性折纸图案需要求解复杂的闭环方程，求解过程十分复杂和困难，这一定程度上限制了刚性折纸的设计。简化刚性折纸图案的机构学模型和求解过程有利于解决上述问题。
        天津大学机械工程学院陈焱教授及其学生博士研究生吕玮琳和彭瑞博士以及索尔福德大学科学工程与环境学院魏国武教授以单个球面四杆机构的运动学为基础，通过将四个相同的球面四杆机构连接成一个单闭合环路，构造了三种基本的单自由度球面四杆机构装配体，并得到了其运动协调条件。然后利用上述运动协调条件，通过改变三种基本装配体中机构的几何参数，得到了上述基本装配体的多种变化类型，每种变化类型均为单自由度，这一方法简化了刚性折纸的机构学模型。接下来，以基本装配体的变化类型为基础，通过添加进一步的几何约束，得到了一种新的刚性折纸图案——螺旋折纸图案。该成果于2019年9月25日发表在期刊Mechanism and Machine Theory第142卷上。

由相同球面四杆机构构成的闭合环路

一种新的刚性新折纸图案（螺旋折纸图案）

        本文提供了一种新的方法得到球面四杆机构的单自由度装配体，并且从中可以得到新的刚性折纸图案，在机器人，智能建筑，机械超材料和航空航天等领域具有广阔的应用前景。

Yan Chen, Weilin Lv, Rui Peng and Guowu Wei, 2019, Mobile assemblies of four-spherical-4R-integrated linkages and the associated four-crease-integrated rigid origami patterns, MMT, Volume 142, 103613 (https://doi.org/10.1016/j.mechmachtheory.2019.103613)