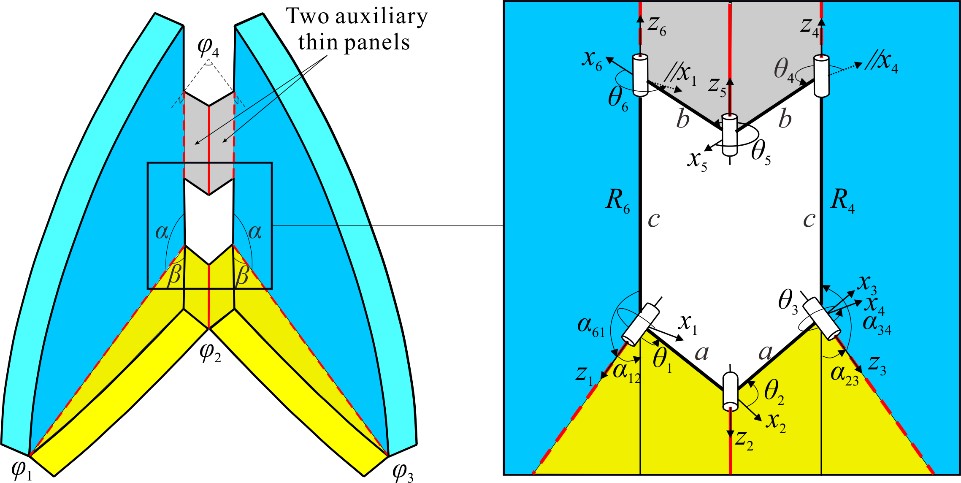
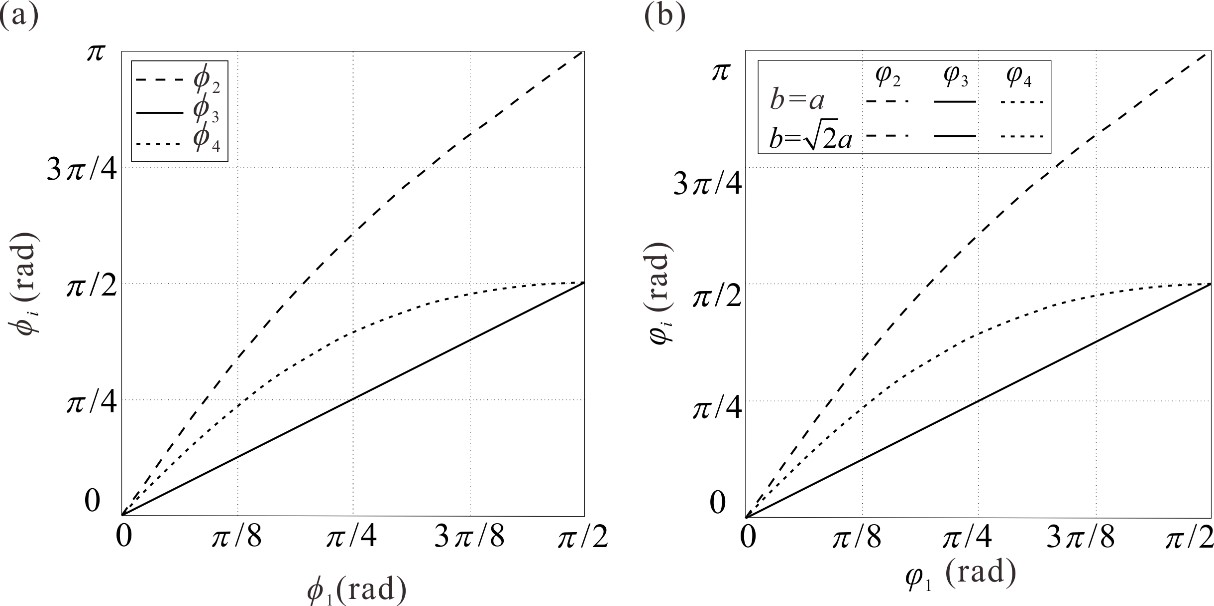
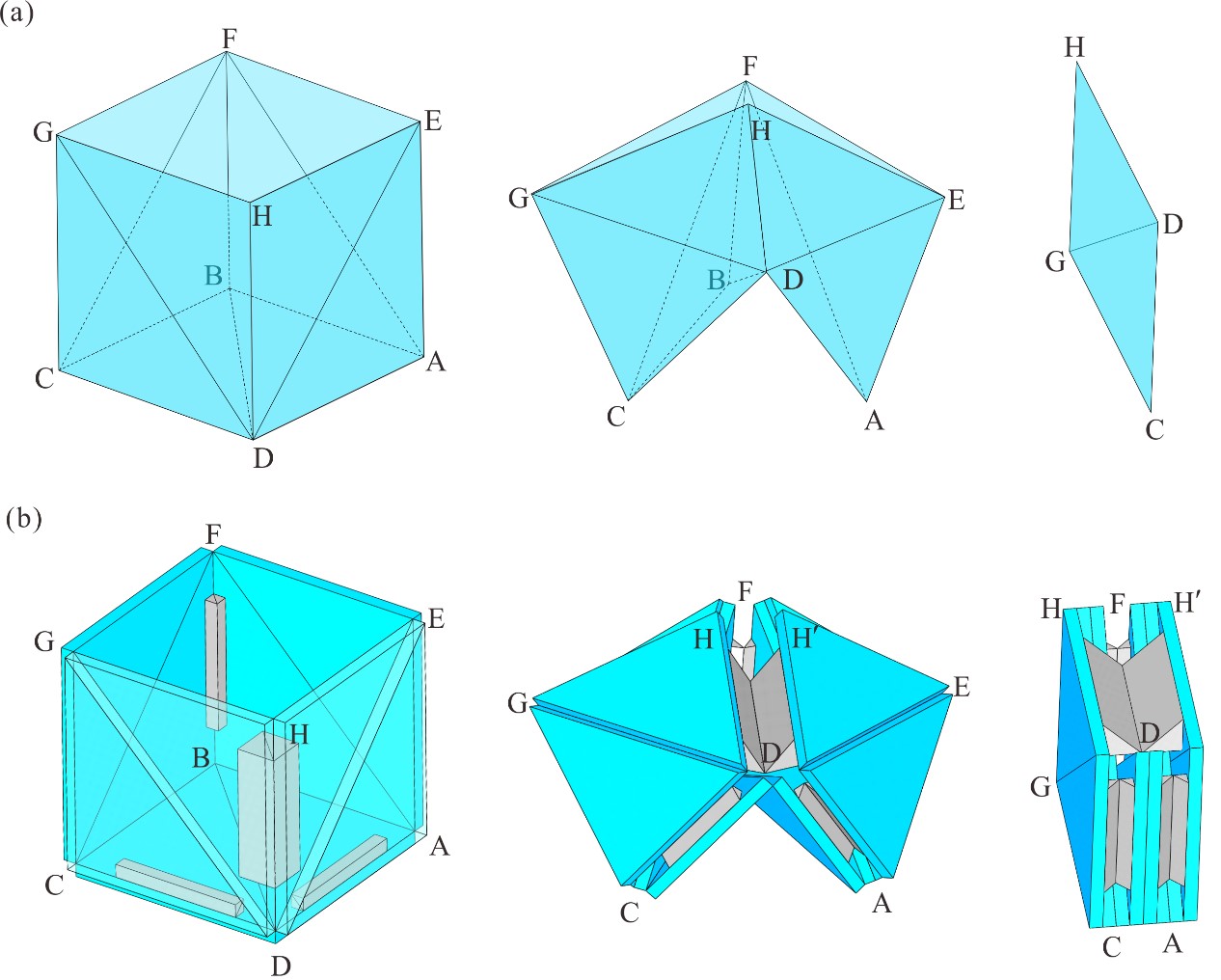
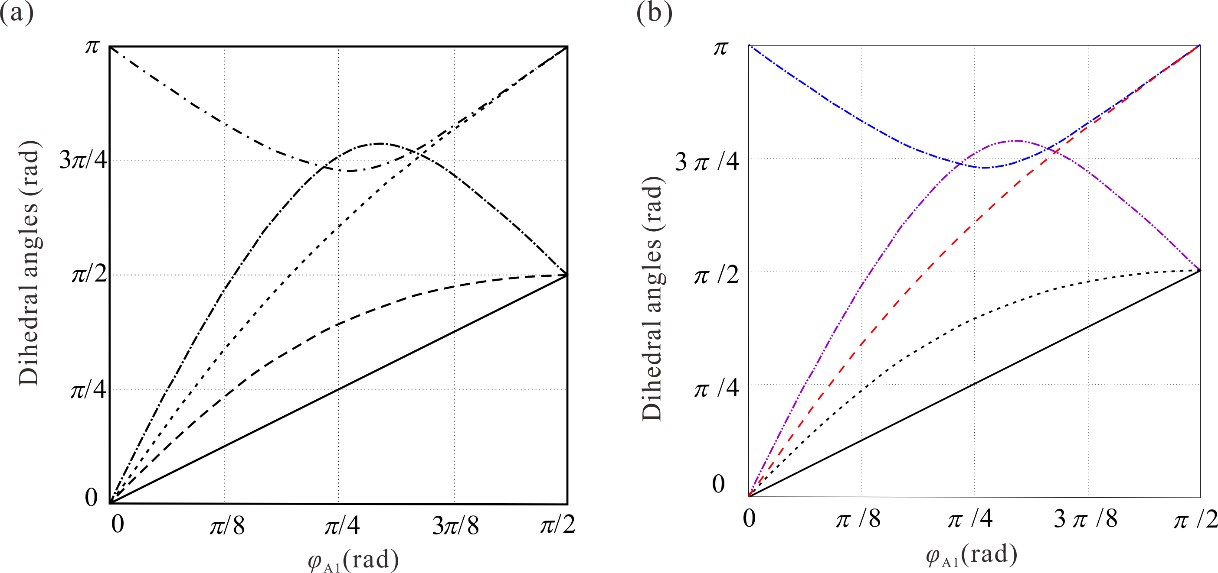
折纸启发的折展结构和机构在航空航天、机器人、医疗设备、机械超材料等领域具有广泛的应用。为了拓展折纸图案在厚板结构中的工程应用，多种板厚容纳方法已被提出。例如，在Miura-ori图案中利用Bennett机构替换四折痕折纸顶点所对应的球面四杆机构，可构建其运动等效的厚板形式。然而，由于严格几何约束的限制，Bennett机构并不适用于一般面对称四折痕折纸顶点的厚板构建。通过建立新的运动学模型，获得具有运动等效特性的厚板顶点以及厚板立方体结构是该文章的主要目的。
        天津大学机械工程学院博士研究生顾元庆与其导师陈焱教授以及索尔福德大学科学工程与环境学院魏国武教授通过引入面对称Bricard机构，提出了一般面对称四折痕厚板顶点的新型构造方法。通过分别求解零厚度折纸顶点与其厚板形式的闭环方程与运动曲线，验证了新型厚板顶点完全保留了其零厚度折纸顶点的运动学行为。

一般面对称厚板顶点(α+β＜π)及其等效的Bricard机构

一般面对称四折痕(a)零厚度折纸顶点与(b)厚板顶点的运动曲线

厚板顶点折叠过程

        将该厚板顶点应用于零厚度折纸立方体图案，构建了新型单自由度可平折的厚板立方体结构。通过分析几何约束和求解所对应空间机构网格的闭环方程，验证了立方体在上述两种构造形式下的运动学行为一致，如下方两组运动曲线所示，揭示了厚板立方体与其零厚度折纸图案之间的运动等效特性。上述等效特性的优势是能够利用零厚度折纸已知的运动学行为来直接控制和规划其厚板运动。

(a)零厚度折纸立方体与(b)厚板立方体结构

(a) 零厚度折纸立方体与 (b) 厚板立方体的运动曲线

        该成果于2021年5月27日被期刊Mechanism and Machine Theory接收，并于6月15日在线发表。该方法将零厚度折纸图案成功转化为厚板等价结构，这为艺术和数学等领域丰富的折纸图案在工程中直接应用提供了极大的便利，并为后续厚板折纸的创新设计提供了新的思路和理论基础。

Yuanqing Gu, Guowu Wei, Yan Chen, 2021, Thick-panel origami cube, Mechanism and Machine Theory, Volume 164, 104411.
(https://doi.org/10.1016/j.mechmachtheory.2021.104411)