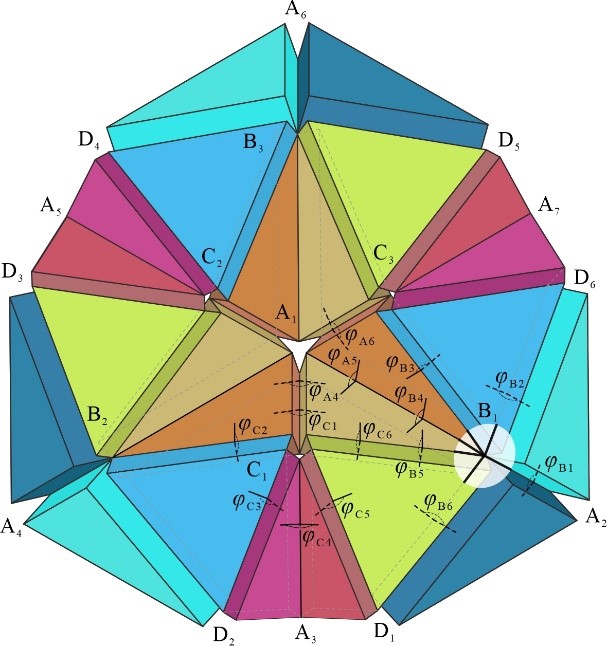
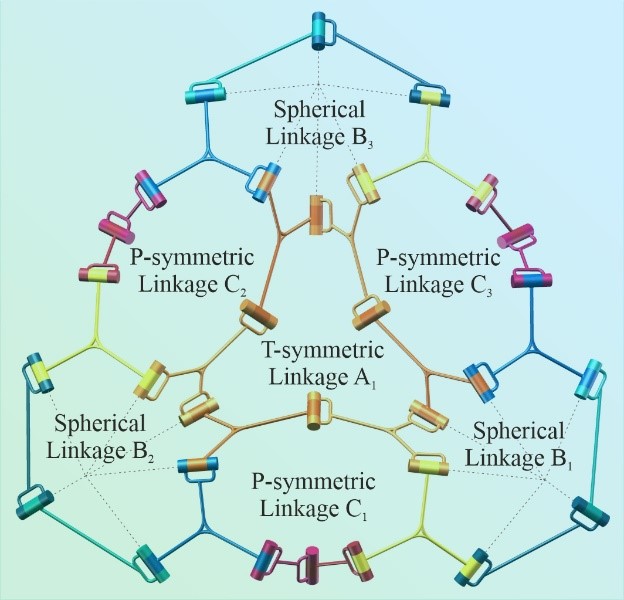
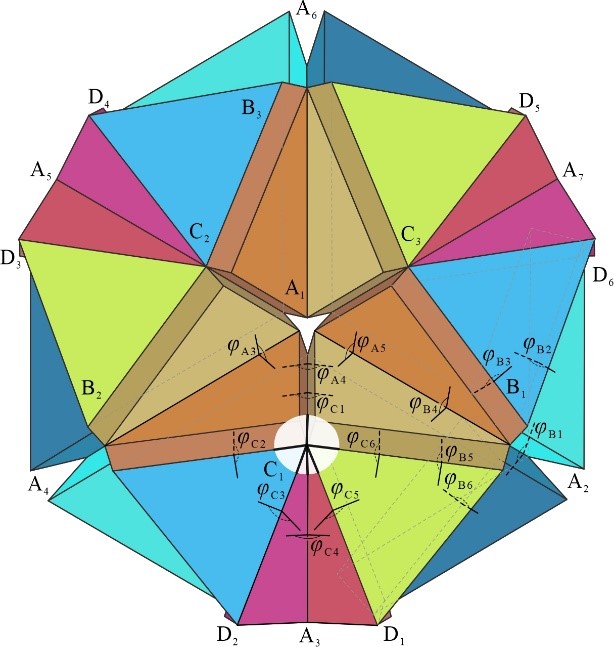
Resch Pattern是由国际著名折纸艺术家Ronald Dale Resch教授于上世纪六十年代发明的一系列折纸阵列图案。其中，三角形Resch Pattern由于具有较好的刚度并能形成各种复杂曲面，受到了各领域学者的广泛关注。然而，多自由的特点使该折纸图案不易于控制，很大程度上阻碍了其折叠功能的实现。因此，降低Resch Pattern的自由度数成为其进一步应用的前提。
        为保持三角形Resch Pattern折叠特点并降低其自由度数，天津大学陈焱教授团队（第一作者杨富富博士现为福州大学机械工程及自动化学院讲师）联合牛津大学由衷教授及美国工程院院士、普林斯顿大学G. H. Paulino教授近期提出了两种单自由度三角形Resch Pattern的厚板折纸模型。
        对三角形Resch Pattern节点进行分类，根据厚板折纸理论找到各类顶点的潜在单自由度厚板形式（单环空间过约束机构）。研究发现，若在三类顶点处均采用厚板形式，将会得到无法运动的刚性结构。在此基础上，通过释放部分约束，得到了三角形Resch Pattern的两种单自由度厚板折纸形式。通过机构运动学推导了所有运动变量之间的关系，并确定了单自由度特性。通过制作实物厚板模型，对研究结果进行了进一步验证。

(a)

(b)

(c)

(a) 方案I及其等效机构，(b) 方案II及其等效机构，(c) 两个方案的实物模型及薄板Resch Pattern的折叠过程

        该成果于2021年11月9日被国际机构学与机器科学联合会（IFToMM）官方期刊Mechanism and Machine Theory接收，并于2021年12月2日在线发表，为探寻多自由度折纸的单自由度形式提供一种新的设计思路，为刚性折纸的进一步应用奠定基础。

Fufu Yang, Miao Zhang, Jiayao Ma, Zhong You, Ying Yu, Yan Chen*, G. H. Paulino*, 2022, Design of Single Degree-of-Freedom Triangular Resch Patterns with Thick-panel Origami, Mechanism and Machine Theory, 169, 104650.
(https://doi.org/10.1016/j.mechmachtheory.2021.104650)