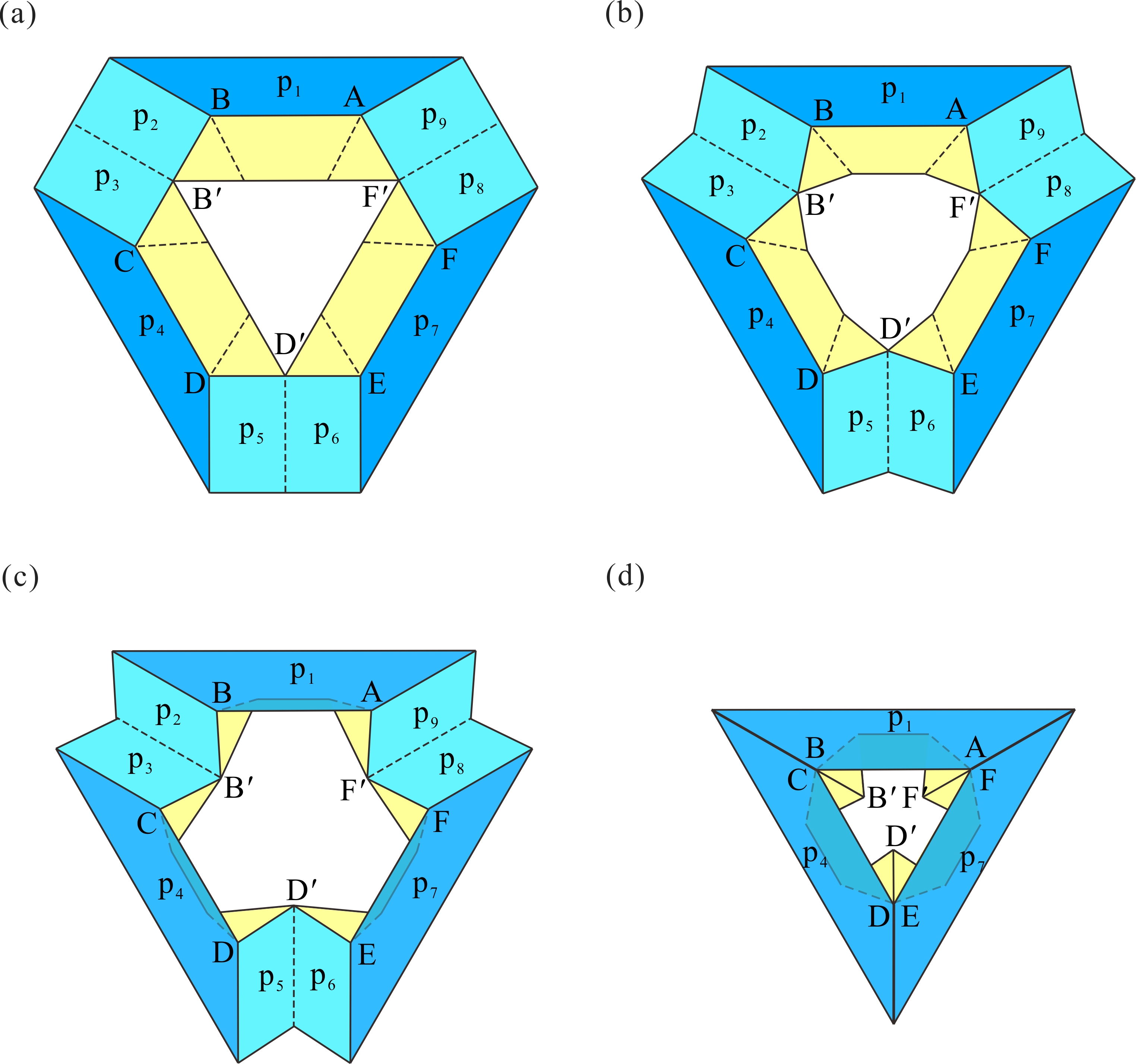
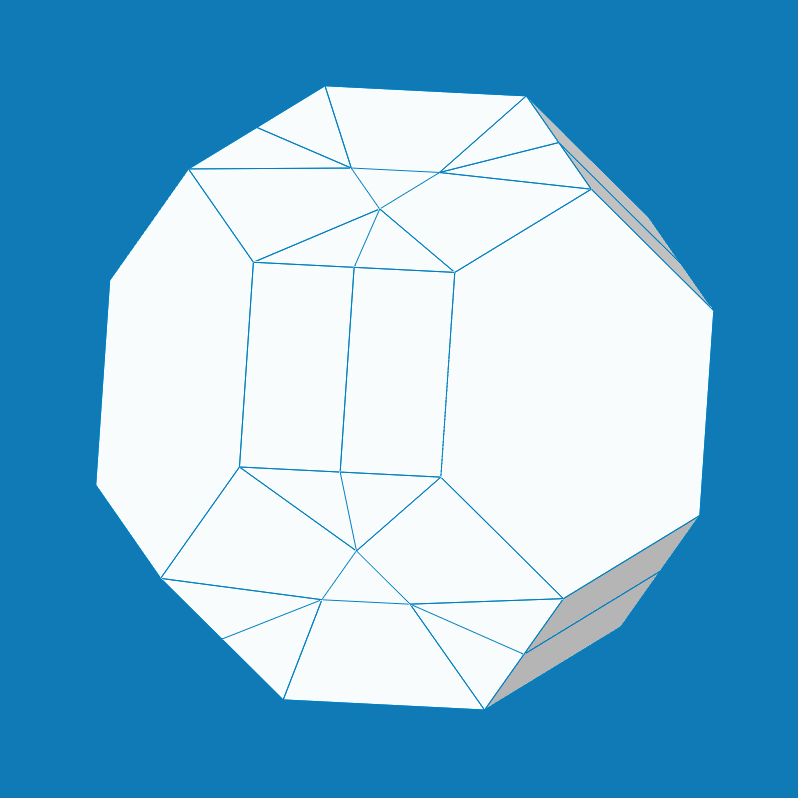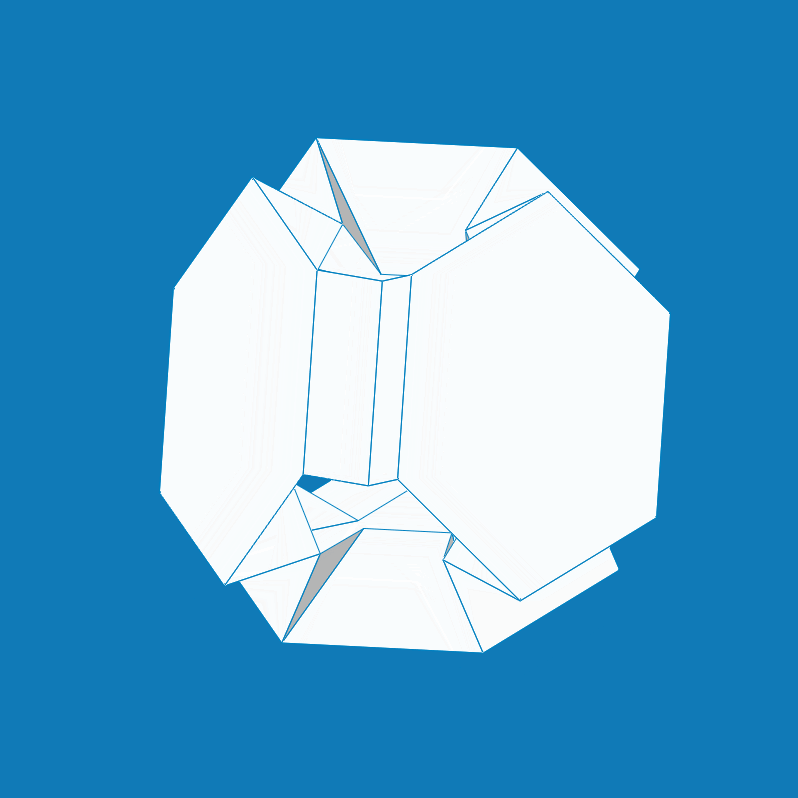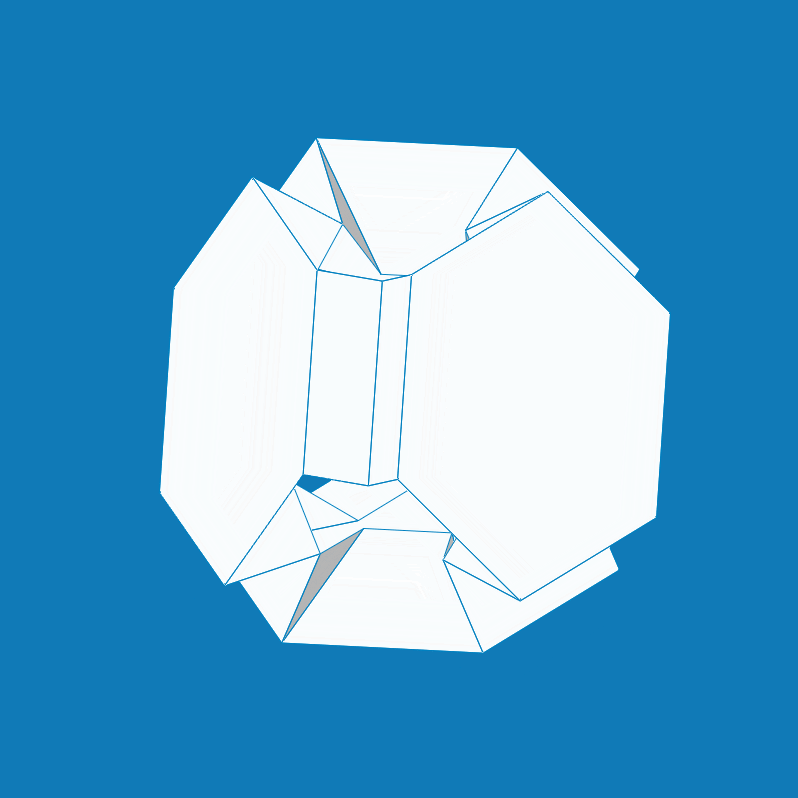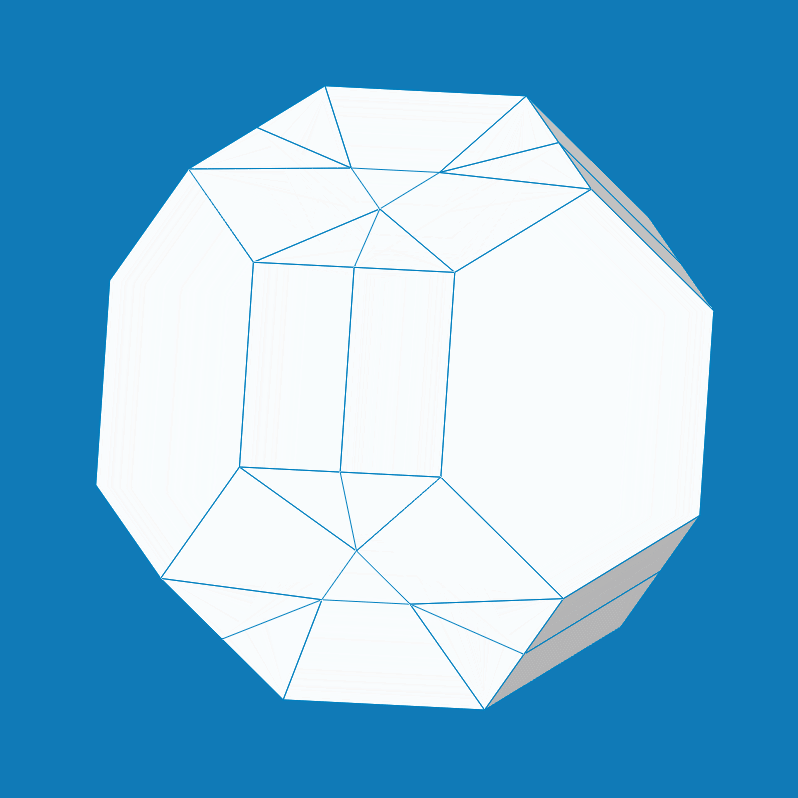
多面体变换是一个很有趣的数学问题，但通过机构运动学理论来实现两种规则多面体之间的单自由度变换却具有挑战性。现有的可折展多面体机构多数是将平面机构或空间机构运动链嵌入至多面体的棱边和表面处，而引入折纸机构的构建策略却很少见。针对以上问题，天津大学机械工程学院博士生顾元庆与其导师陈焱教授提出了一种三重对称折纸同步机构，以此构建出了一系列单自由度径向折展的折纸多面体机构，并基于几何缩短操作实现了九种多面体变换方案。

        首先，将成对的球面四杆机构(A-B, C-D, E-F)嵌入至三自由度的空间九杆机构(p1-p9)以提供额外的运动约束，构建出一种具有三重对称运动特性的单自由度折纸同步机构，其中三个平台(p1, p4, p7)在折叠过程中可保持精确径向直线运动(图1)。

图1 三重对称的单自由度折纸同步机构

        对三种具有不同对称特性的多面体进行表面划分，将折纸同步机构作为构建胞元并按照相应的对称性嵌入至多面体表面，综合出三种单自由度径向折展的折纸多面体机构(图2)。每一种折纸多面体在同步径向折叠的同时均完成了多面体之间的变换，且自身对称性时刻保持不变。

图2 三种单自由度径向折展的折纸多面体机构。(a) 大斜方截半四面体与截角四面体；(b) 大斜方截半立方体与截角立方体；(c)大斜方截半二十面体与截角十二面体。

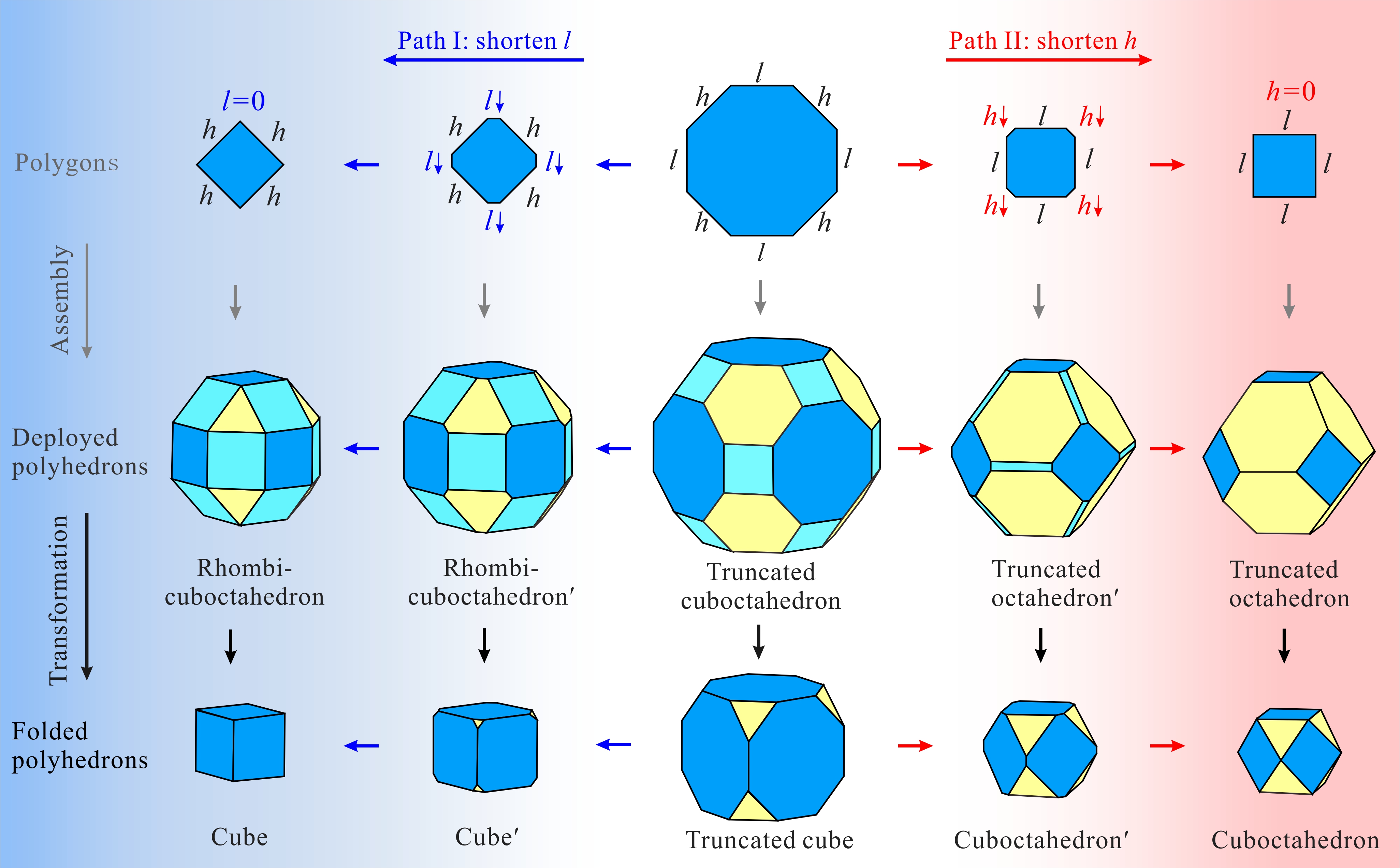
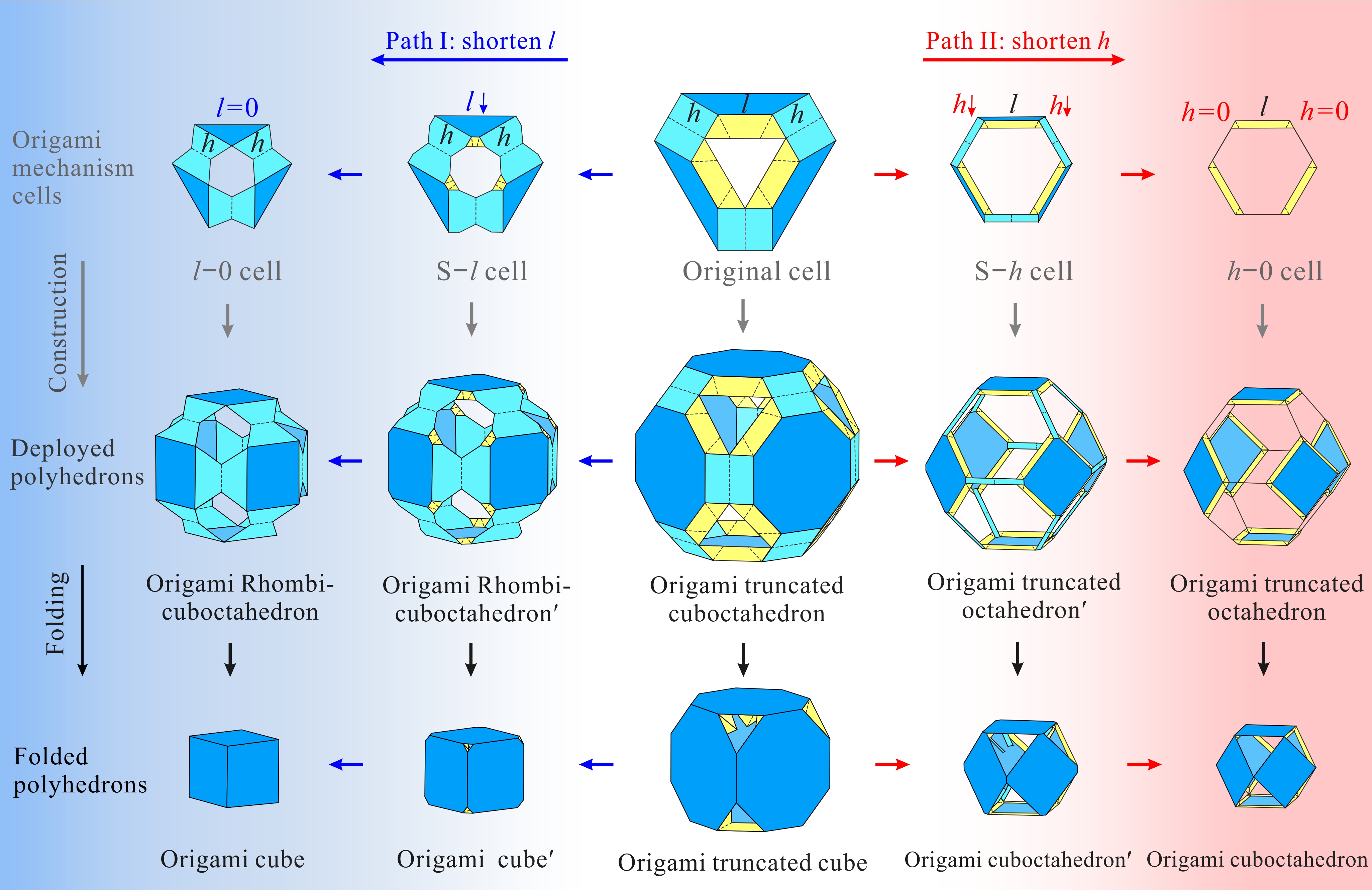
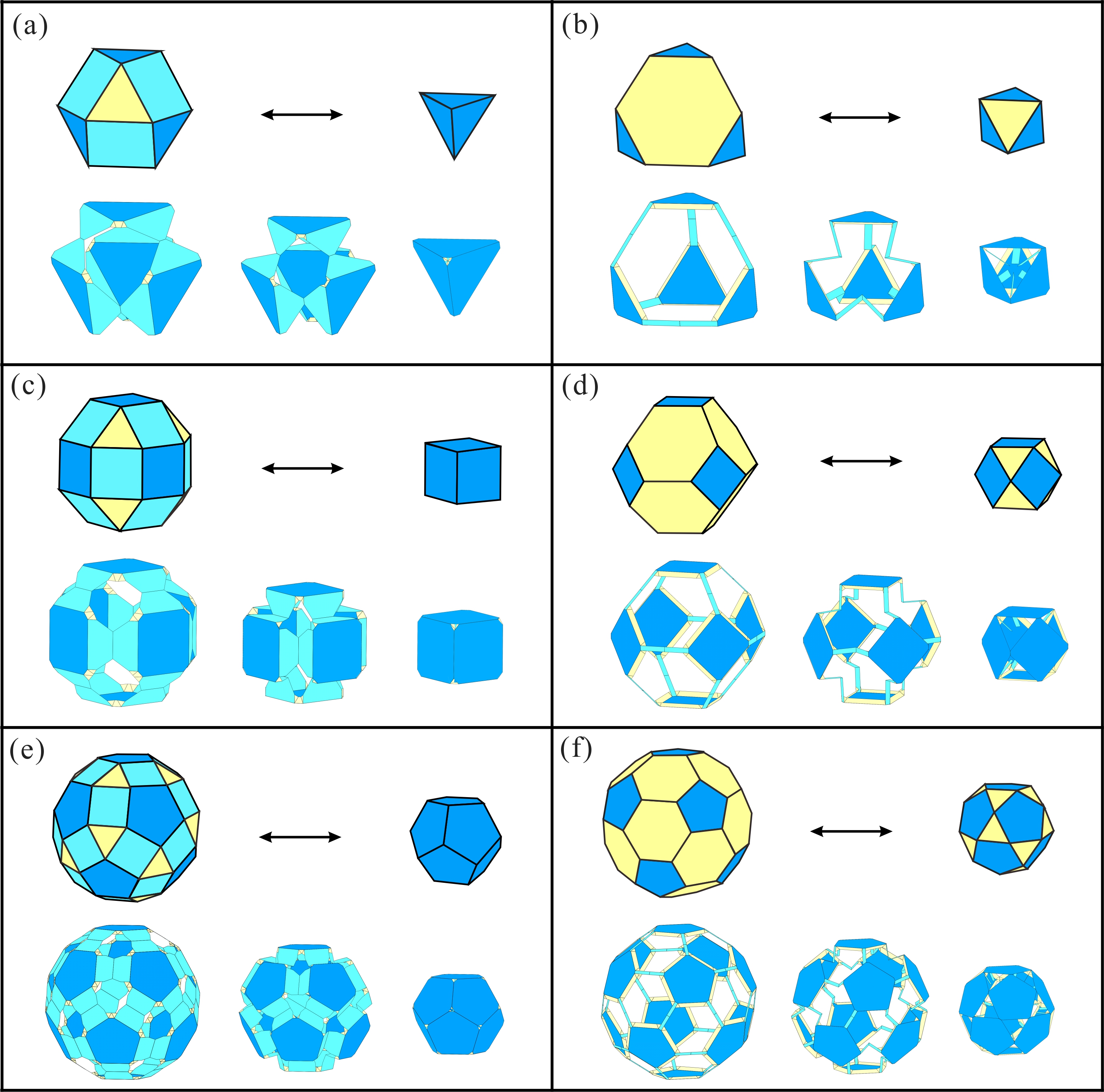
        以大斜方截半立方体(图2b)为例，图3展示了多边形及其组成的多面体在几何维度的缩短操作：第一行对原始八边形沿着两条路径分别进行缩短，第二行和第三行分别为组成的多面体展开形态与折叠形态。在此基础上，图4展示了将几何缩短映射至多面体机构的变化结果：第一行对折纸机构胞元分别进行缩短，第二行和第三行分别为构建而成的多面体机构展开状态与折叠状态。此时，在大斜方截半立方体机构(truncated cuboctahedron)的基础上分别获得了小斜方截半立方体机构(rhombicuboctahedron)与截角八面体机构(truncated octahedron)。由于上述缩短操作只针对结构几何尺寸，多面体机构拓扑并未改变。因此。基于机构拓扑同构性，缩短操作所衍生出的多面体机构仍然具有单自由度径向折展的运动特性。

图3 几何维度上的缩短操作

图4 折纸多面体的结构变化

        为了进一步探索更多变换方案，将图4的结构变化方法应用于图2中的折纸多面体，共获得了其余六种折纸多面体的单自由度变换方案(图5)，其中每一行的两个方案都具有相同的对称性与机构拓扑同构性。

图5 其余六种折纸多面体变换方案。(a)小斜方截半四面体和四面体；(b)截角四面体与截半四面体；(c)小斜方截半立方体和立方体；(d)截角八面体与截半八面体；(e)小斜方截半十二面体和十二面体；(f)截角二十面体与截半二十面体。

        该成果于2023年2月12日被期刊Mechanism and Machine Theory接收，并于2月18日在线发表。此研究所提出的折纸多面体机构及其变换方案为空间折展结构与多功能超材料的创新设计提供了新的灵感与思路。

Gu Y, Chen Y*. Deployable origami polyhedrons with one-DOF radial motion. Mechanism and Machine Theory, 2023, 184, 105393.
(https://doi.org/10.1016/j.mechmachtheory.2023. 105293)