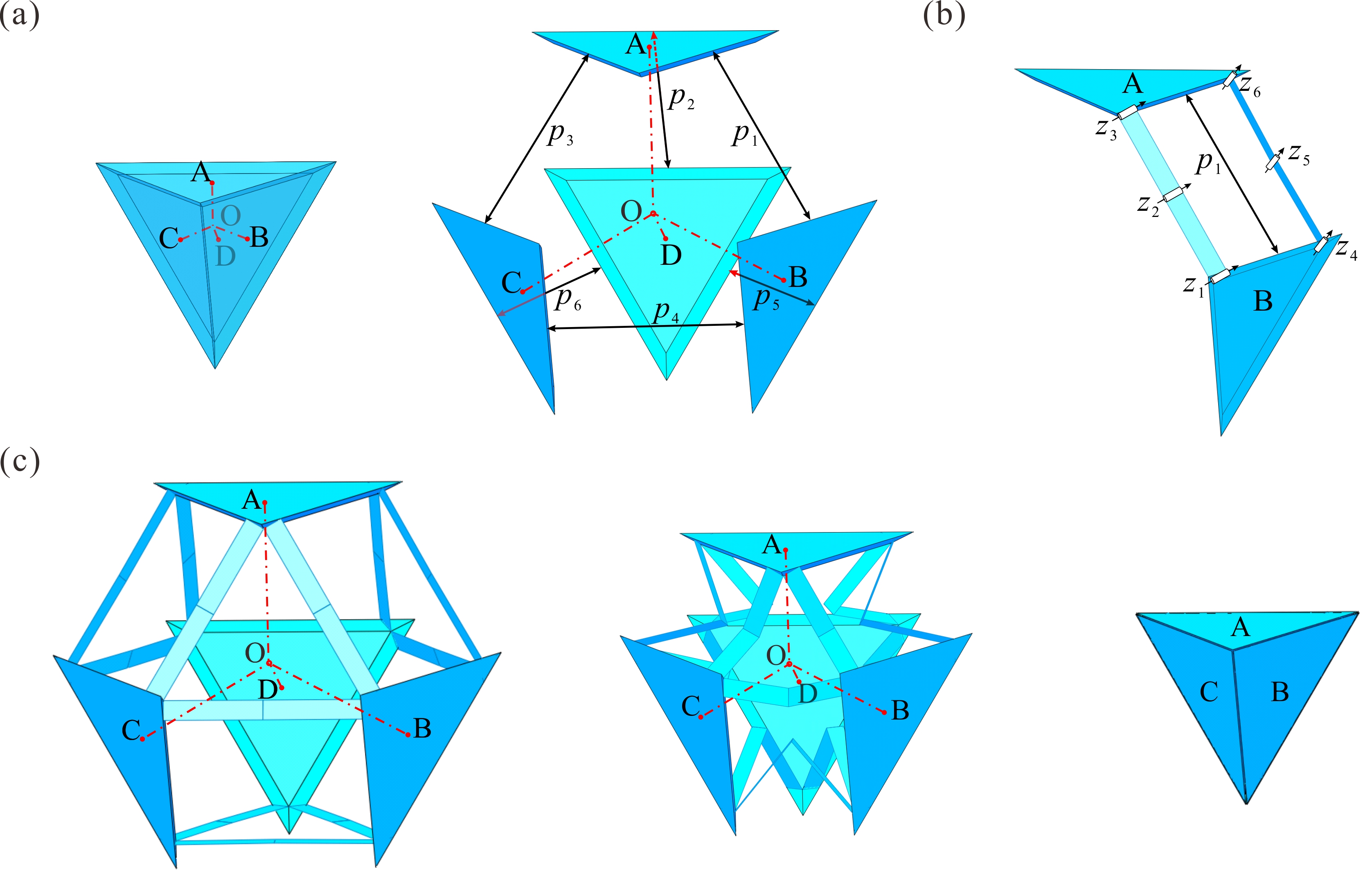
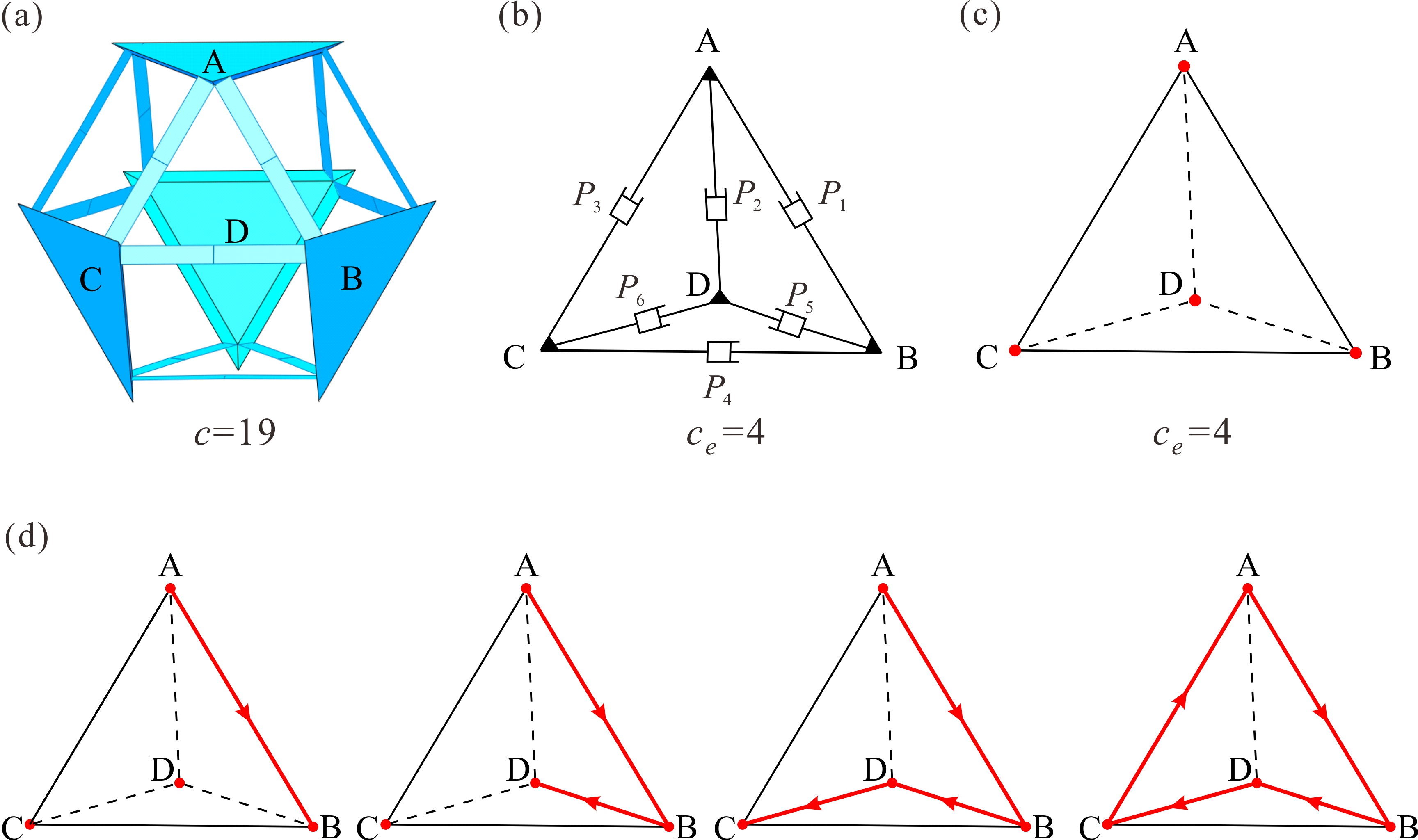
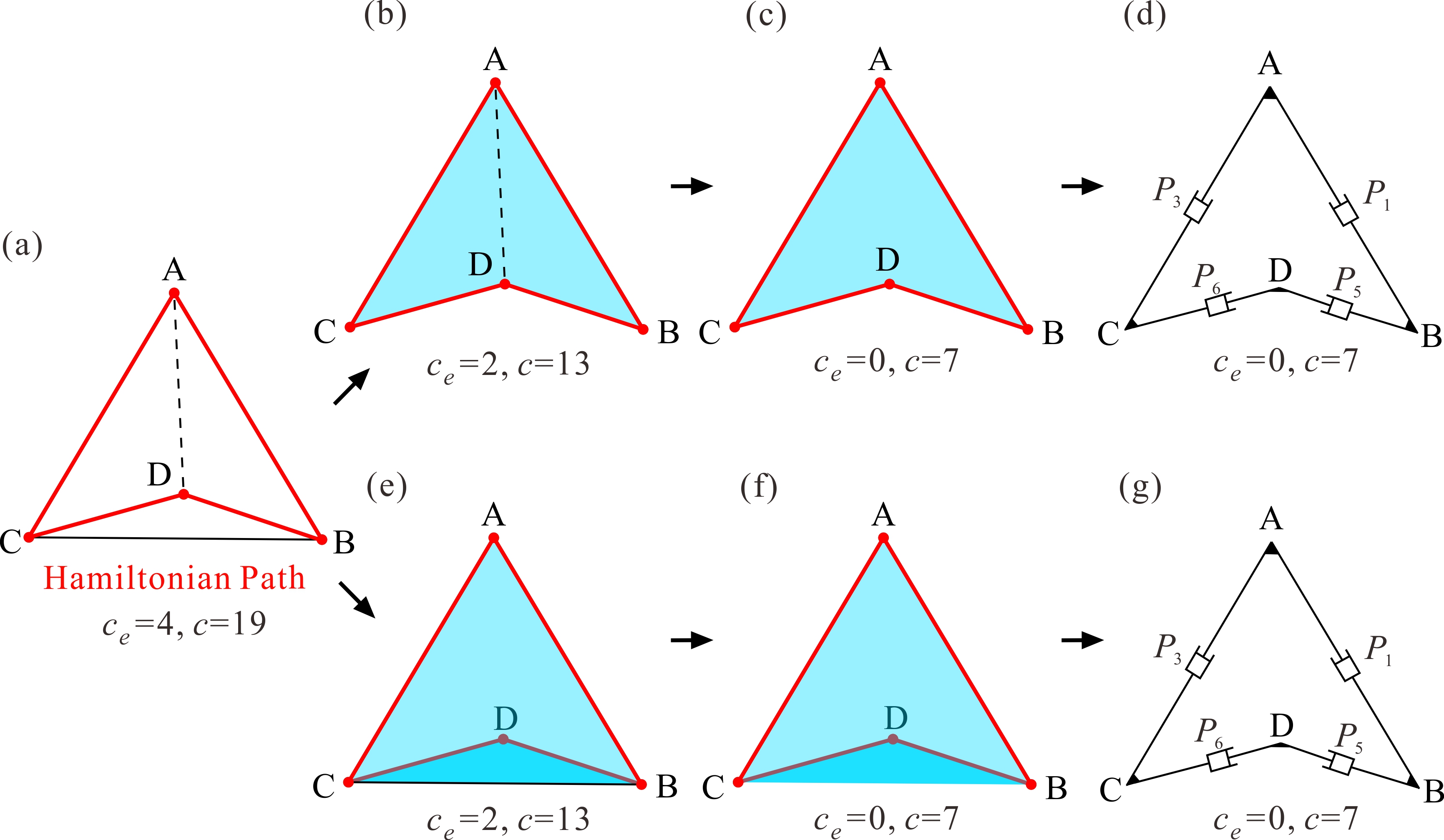
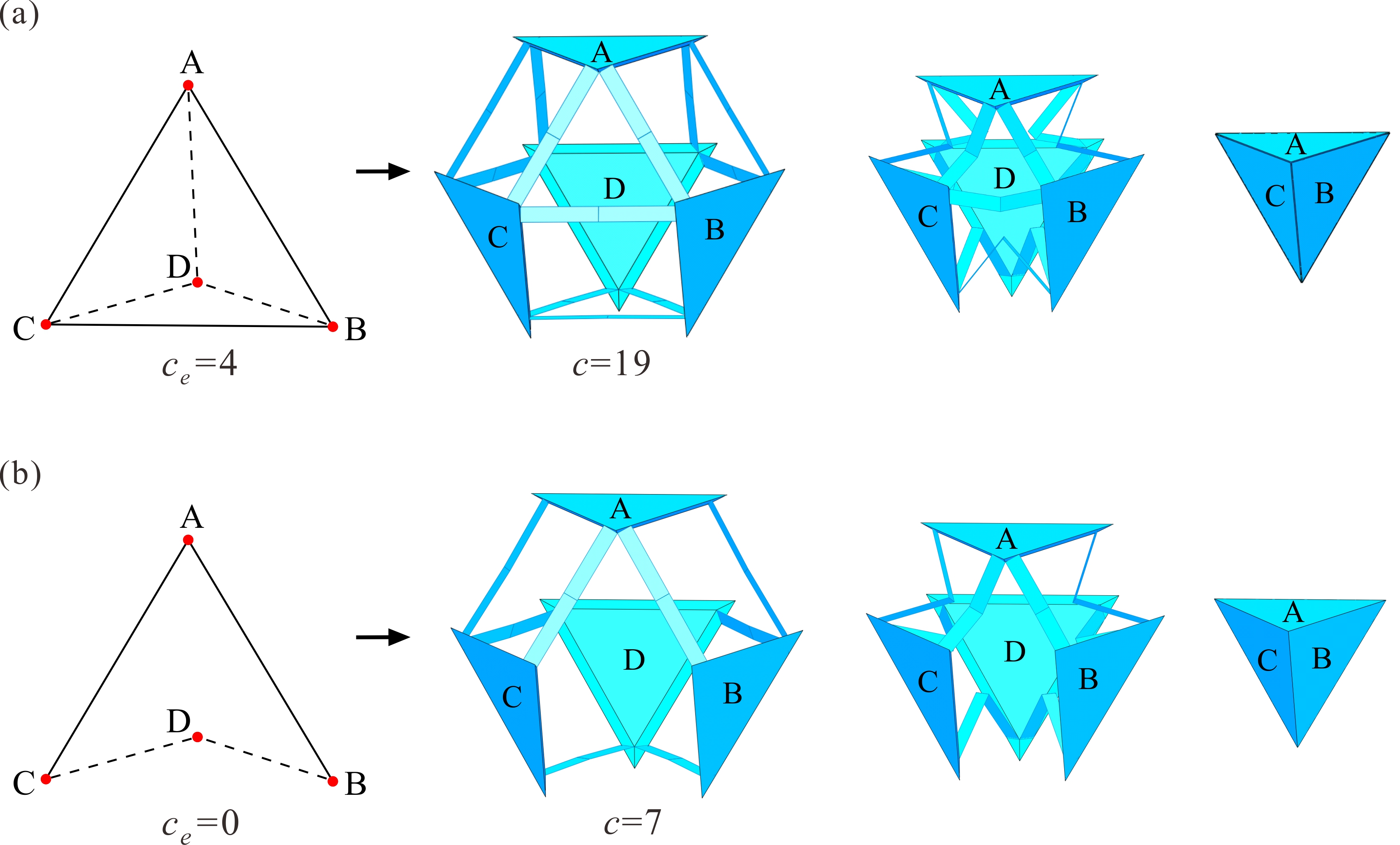
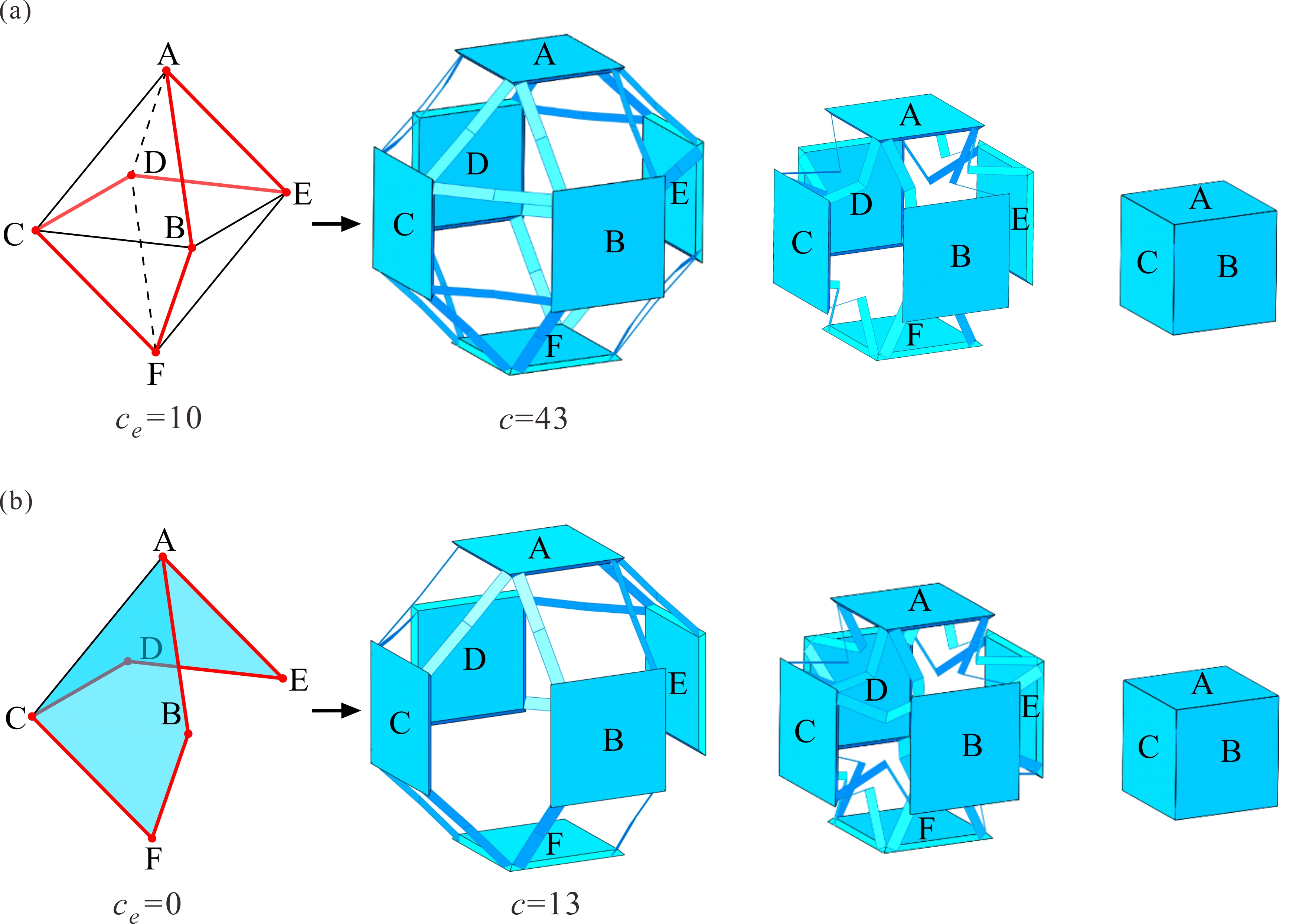
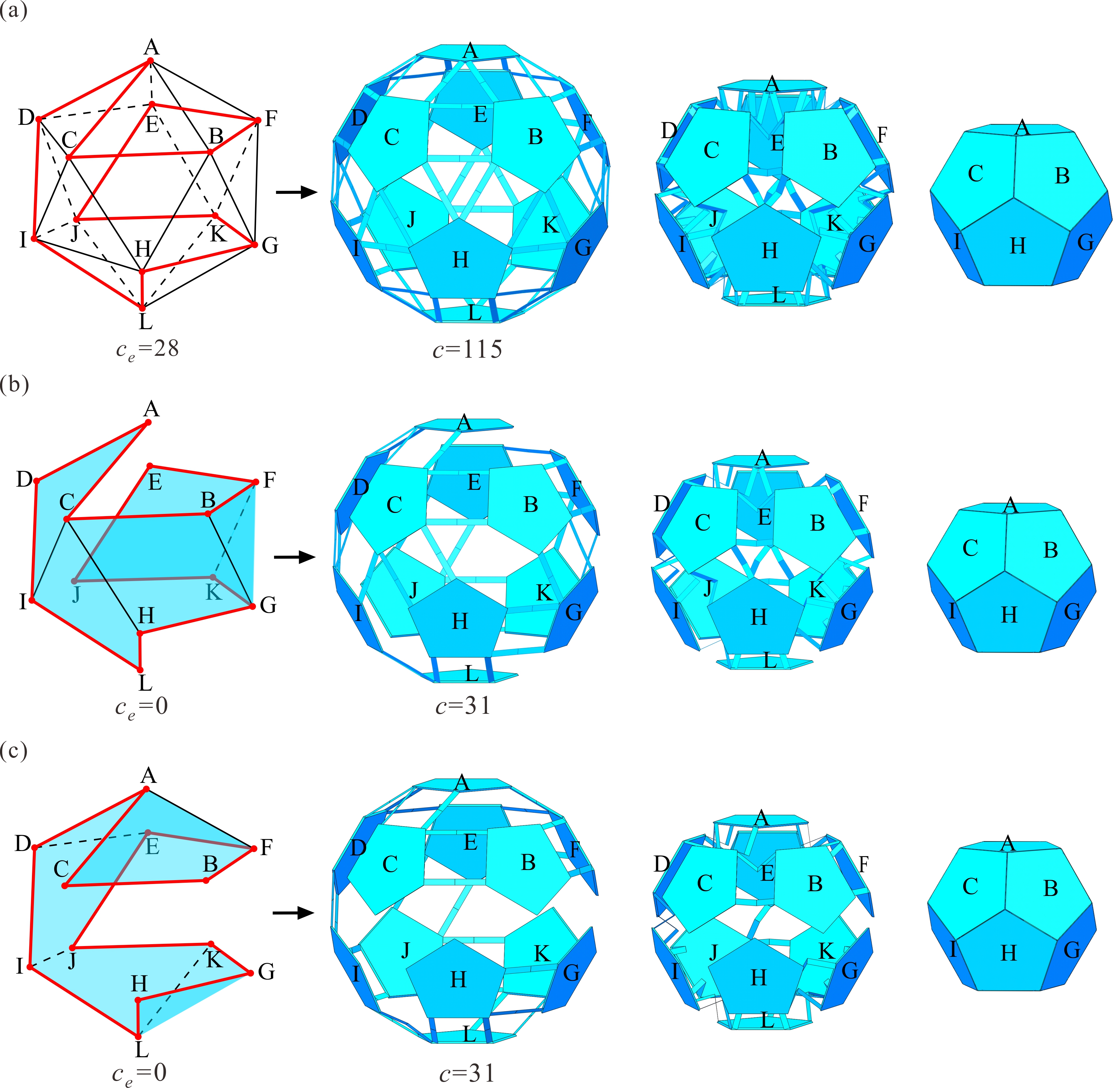
折展多面体的设计融合了机构运动学和立体几何学的巧妙灵感，但通过运动学策略来实现两种规则多面体之间的单自由度变换依然面临挑战。此外，大多数多面体机构都为空间多环路过约束机构，该机构本质阻碍了其工程化发展，在运动学等价基础上的过约束消减方法则成为了亟待解决的运动学理论难题。针对以上问题，天津大学陈焱教授与索尔福德大学魏国武教授合作，基于Sarrus机构设计了一系列单自由度径向折展多面体，并基于哈密尔顿路径提出了多环路过约束机构的过约束消减方法, 在运动学等价的基础上大幅降低了机构过约束度。

        首先，对于具有T_d对称性的四面体，将其四个平台进行相对于体心的几何展开操作，此时相邻的两两平台间以直线运动的方式相互远离，如图1a中p_i所示。为此，选取图1b所示的具有精确直线运动的Sarrus连杆机构作为折展多面体的基本机构单元。如图1c所示，将Sarrus连杆机构嵌入至两两平台间以满足几何上的相对直线运动要求，通过综合六个机构单元构建了单自由度四面体机构。所构建的四面体机构在单自由度径向运动的同时，完成了小斜方截半四面体(展开态)与四面体(折叠态)之间的规则变换。

图1 单自由度折展四面体机构的构建

        运动学分析表明该四面体机构具有19个过约束数(c=19)，为了简化分析计算与拓扑操作，将一个Sarrus机构等效为一个移动副机构，那么整体四面体机构(图2a)就可等效为四面体移动副机构(图2b)，其等效过约束数c_e=4，并在图2c给出了该机构的等效四面体拓扑图。同时，机构拓扑消减的前提条件可总结为：(1)拓扑图中的每个点至少需要两个连线以构成闭环机构；(2)包括自由度在内的机构运动学特性不发生改变。在此条件下，引入了哈密尔顿路径这一数学概念，其具有如下两个特征：(1)图中每个点只能被穿过一次；(2)必须为闭合的环路。以四面体唯一的哈密尔顿路径为例进行说明，其生成过程如图2d所示。所以，在多面体的拓扑图上引入哈密尔顿路径，有望解决过约束消减这个运动学理论难题。

图2 等效的四面体机构及其哈密尔顿路径

         接下来，利用哈密尔顿路径进行四面体机构的拓扑消减操作。如图3a红线所示的哈密尔顿路径把四面体拓扑图分成了两个相同的半壳，第一行图3b中相当于去除了线段BC，此时c_e=2。在消减前提下只能继续考虑去除路径内部的线段AD，如图3c所示，此时的等效过约束数c_e=0。该空间四边形ABDC所表示的机构的自由度与运动特性都没有改变，所以图3c所示的机构拓扑图可视为四面体机构的最简约束形式，其等效的移动副机构如图3d所示。由于四面体对称性，第二行中图3e-g给出的消减结果与第一行中图3b-d的结果相同。将最简拓扑图映射至Sarrus机构的形式，图4分别给出了消减前后的原始四面体机构和最简约束形式，在运动学等价的基础上过约束数由19降为7。

图3 四面体机构的过约束消减

图4 运动等价的四面体机构及其最简约束形式

        类似的，通过综合十二个Sarrus机构，可构建出具有O_h对称性的立方体机构(图5a)。接着，利用得到的单自由度空间四边形作为基本单元，并研究了其对偶八面体的两条哈密尔顿路径，对非最简形式进行排除后只获得了一种最简立方体机构拓扑(四边形ABFC和ACDE通过线段AC相连)。在保留原始单自由度径向运动的基础上，过约束数由43降为13 (图5b)。

图5 运动等价的立方体机构及其最简约束形式

        最后，基于三十个Sarrus机构，图6a展示了具有I_h对称性的十二面体机构，原始机构具有115个过约束(c=115)。该机构的等效拓扑图为二十面体，虽然具有十七种不同的哈密尔顿路径，但是所提出的约束消减方法依然能快速有效的获得所有最简机构。以图6a中的一条路径为例，将二十面体分成两个不同的半壳，并通过依次布置五个四边形最简单元，可分别得到图6b和图6c中两个不同的最简形式，等效过约束数均为c_e=0。分别将两个最简拓扑图映射至Sarrus机构形式, 同样在单自由度等价运动的基础上，过约束数均由115降为31。以同样的消减方式，详细讨论了其拓扑二十面体所具有的十七种不同的哈密尔顿路径，最终可获得十九种最简十二面体机构。

图6 运动等价的十二面体机构及其最简约束形式

        上述研究的两篇论文在2023年12月22日在线发表于Mechanism and Machine Theory期刊。论文的共同通讯作者为天津大学陈焱教授与英国Salford大学魏国武教授，第一作者为天津大学博士生顾元庆，第二作者为天津大学张霄博士。此研究建立了新型折展多面体的设计准则，提出了基于哈密尔顿路径的过约束消减方法。不仅为折展多面体机构的创新研究奠定强有力的理论基础，也为其工程化发展提供有效的技术支撑。

1. Gu Y, Zhang X, Wei G*, Chen Y*. Sarrus-inspired deployable polyhedral mechanisms. Mechanism and Machine Theory, 2024, 193, 105564.
(https://doi.org/10.1016/j.mechmachtheory.2023.105564)
2. Gu Y, Zhang X, Wei G*, Chen Y*. Hamiltonian-path based constraint reduction for deployable polyhedral mechanisms. Mechanism and Machine Theory, 2024, 193, 105563.
(https://doi.org/10.1016/j.mechmachtheory.2023.105563)