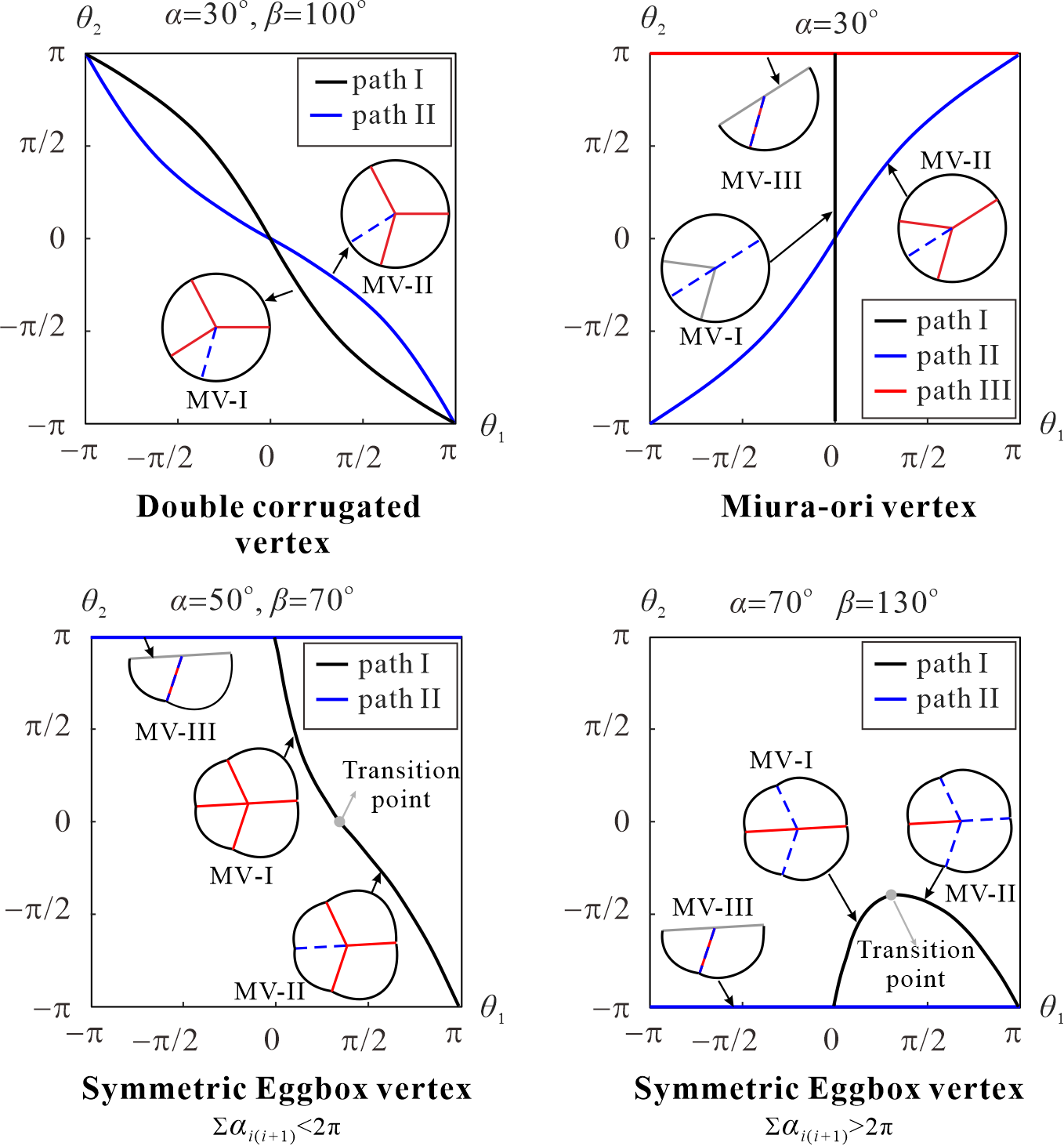
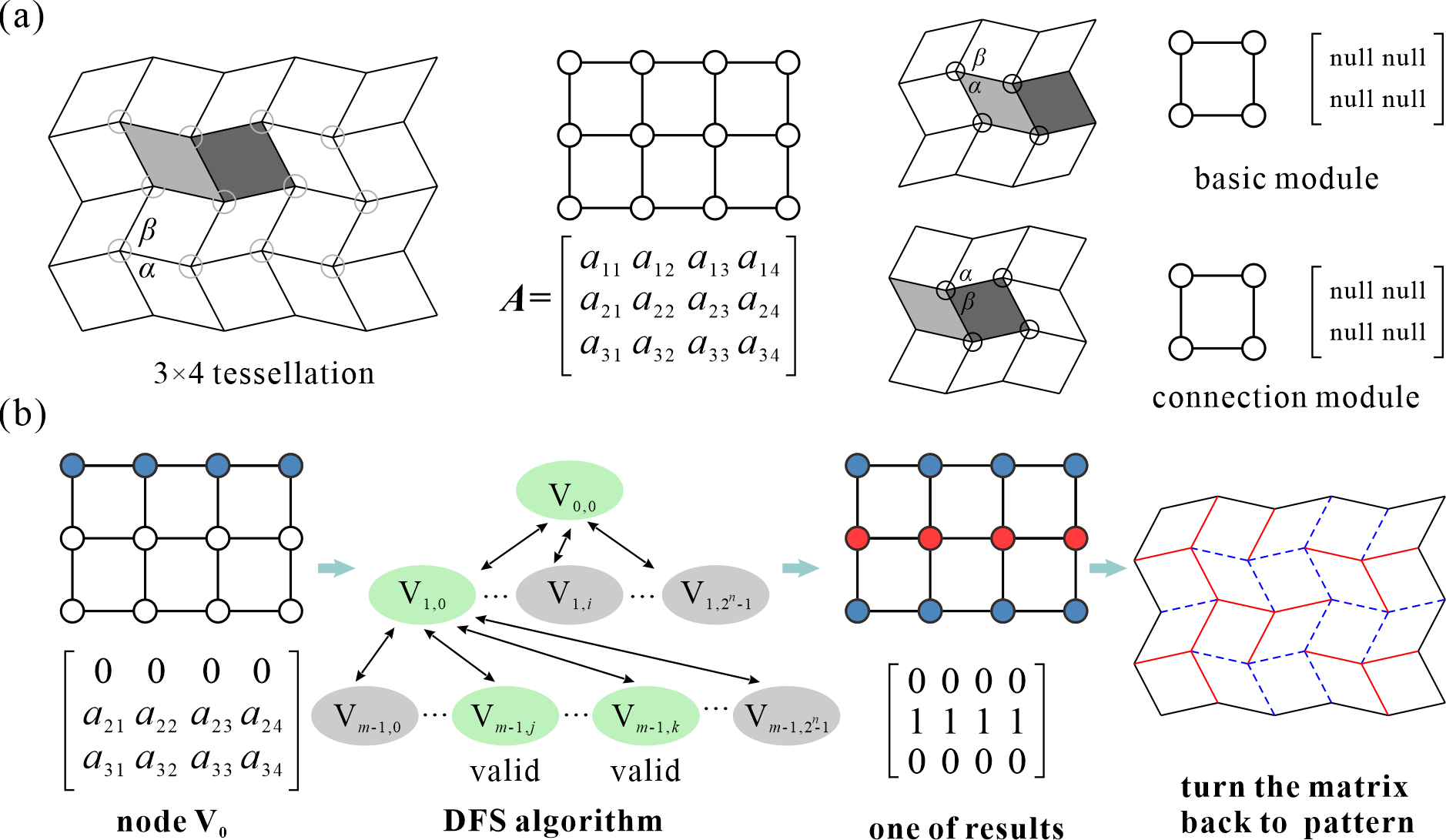
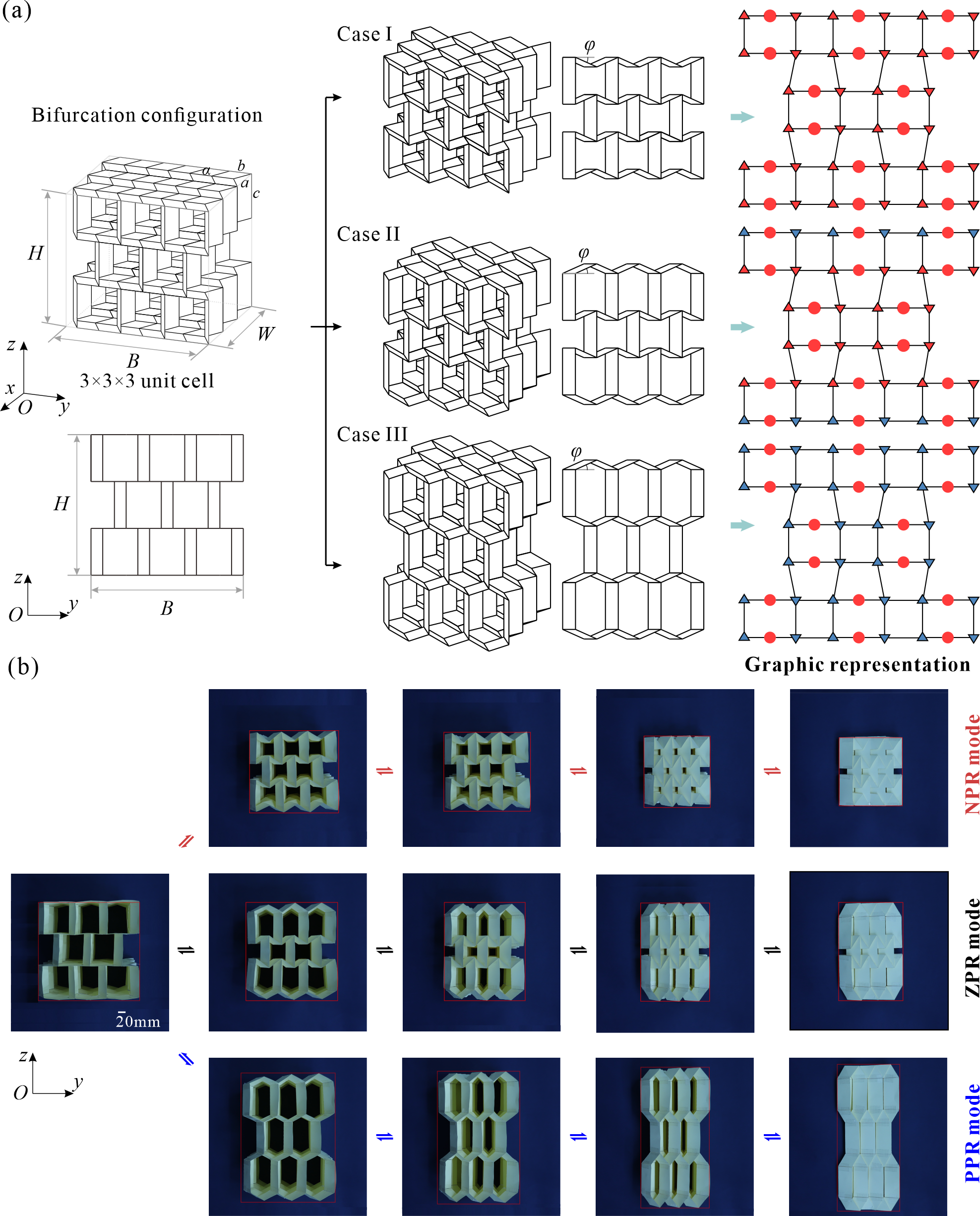
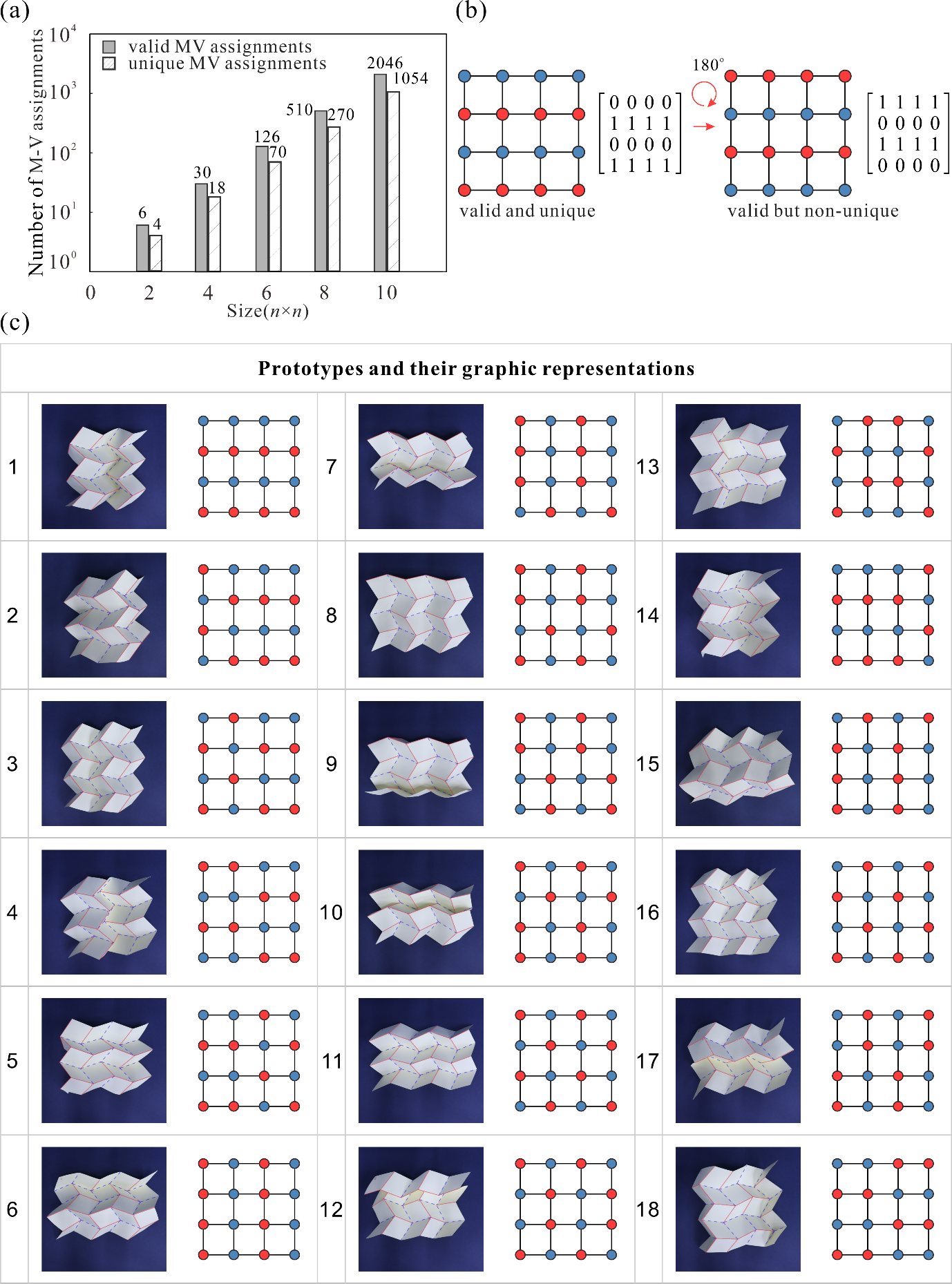
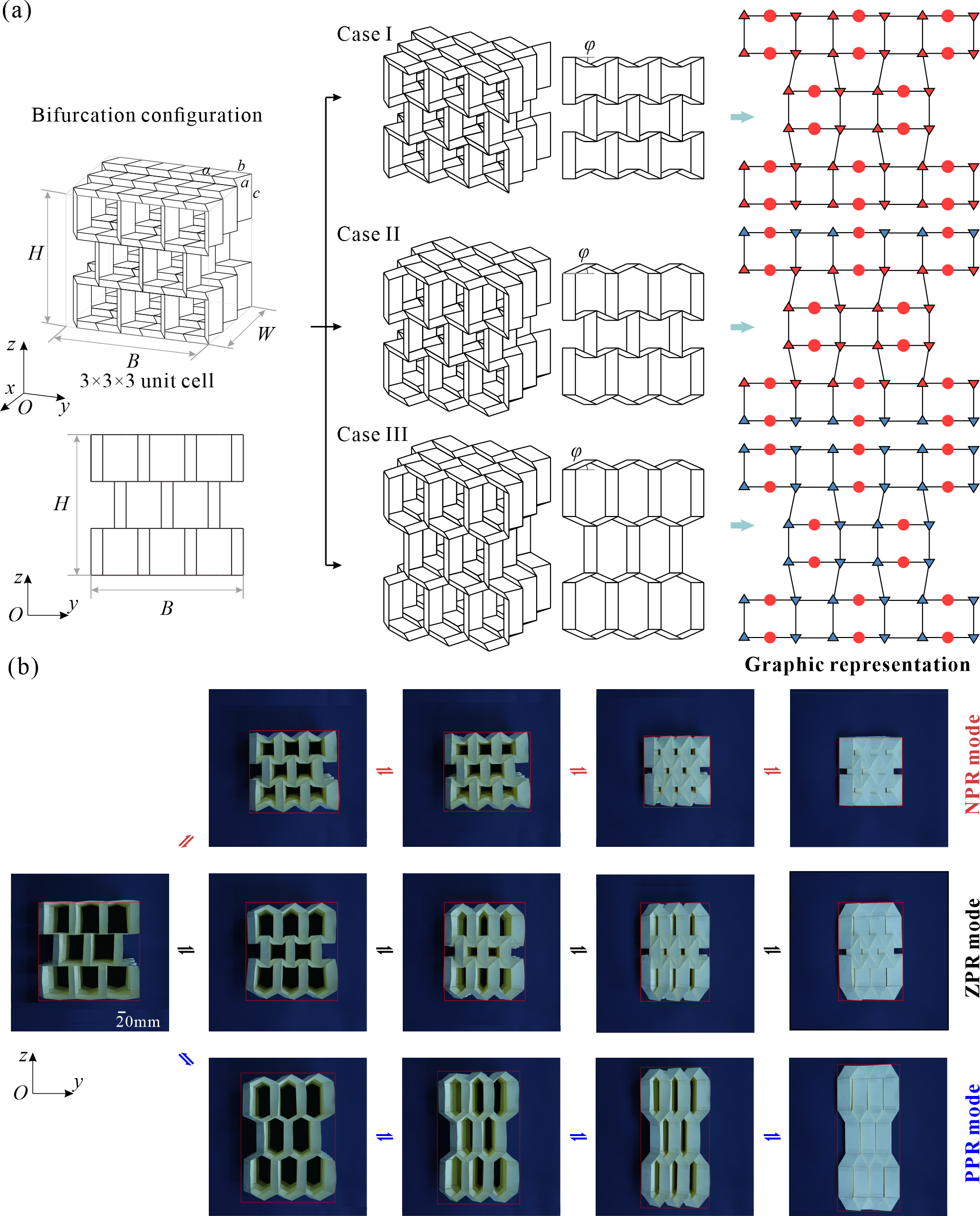
刚性折纸结构可以在面板没有形变的前提下，仅通过折痕的旋转，就将二维平面纸张折叠成复杂的三维立体结构，在可展结构、机械超材料等领域的取得了广泛应用。折痕通常划分为“山折线”和“谷折线”，它们的分布直接决定了折纸结构形态。一旦完成加工，折纸结构中折痕的位置就唯一确定。因此传统的折纸结构只能在单一的折叠态和展开态之间变换。最近的研究表明，通过折痕拓扑变化（包括山谷折痕的转换、折痕的激活与休眠等），可以实现可变构型的可重构折纸，赋予了单一结构多种功能，使其能够在不同环境和任务下进行适应，展现出巨大的应用潜力。然而，在数量众多的刚性折纸图案中，哪些图案可以实现山谷线重构，有多少种重构方式，都是悬而未决的问题。因此，解决精准辨识折纸单元，尤其是其大型2D和3D镶嵌的所有重构路径这一挑战变得尤为重要。
        近日，天津大学陈焱教授课题组以四折痕折纸顶点及其镶嵌为研究对象，开发了一套结合机构网格运动协调条件与图形表达的通用算法，可以在大型2D和3D折纸镶嵌中精准辨识所有满足刚性可折叠性的山谷线分布方案并去除重复构型。该成果于2024年3月25日在线发表于国际著名期刊International Journal of Mechanical Sciences。论文的通讯作者为天津大学陈焱教授，第一作者为天津大学博士生刘伟奇，第二作者为天津大学智能与计算学部硕士生曹颂。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

        首先，四折痕折纸顶点的折痕拓扑变化可以等价为球面四杆机构的运动分叉，不同的山谷线分布方案对应机构的不同分叉路径。因此，通过推导Miura， double corrugated和eggbox这三种最常用的折纸顶点对应的球面四杆机构的运动学逆解，就可以建立每个顶点的运动学路径与山谷线之间的映射关系，如图1所示。

图1 四折痕折纸顶点的运动学路径与山谷线映射关系

        随后，如图2所示，将不同折纸顶点的山谷线用形状、颜色加以区分，并采用2进制的计算机语言表达。例如，double corrugated折纸图案中，0表示该顶点山谷线I（蓝色圆圈），1则表示该顶点山谷线II（红色圆圈）。再采用模块化的思想，提取了诸多2D镶嵌中折纸顶点形成的独立环路。利用球面四杆机构装配体的运动协调条件，就可以迅速求解由四折痕顶点形成的折纸环路的所有山谷线分布方案，并转化相应数量的为2×2的矩阵。从而建立了一个丰富的图形库，包含18种几何参数不同的典型模块。可以看到，这些模块既涵盖了仅由Miura， double corrugated和eggbox顶点组成的图案，还包括了这些顶点混合形成的图案。

图2 折纸顶点及其18种典型环路的图形表达

         如果仍然采用纯机构学的方法求解大型2D折纸镶嵌的运动协调条件方法来分析山谷线重构。这意味着要在一个多环路径机构网格中精准辨识所有分叉路径，不仅效率低下、而且分析难度巨大。
        所以，作者把大型2D折纸镶嵌被抽象为棋盘格，并把寻找所有满足刚性可折叠性的山谷线分布方案这一挑战转换为棋盘着色问题，并通过深度优先搜索算法进行遍历求解（图3和图4）。以图3中的double corrugated折纸图案为例，该图案包含2种模块，分别是基本模块和连接模块，对应图形库中的模块1和模块2（图2b）。通过图2中的图形库可以看到，每种模块对应的颜色分布均需满足图形库中的6种既定规则。然后深度优先搜索算法会遍历搜索树每一层，确保任意一个2×2的子矩形赋值满足这些规则。图形规则及其赋值矩阵极大地减少了搜索树的节点，降低了搜索空间，实现了算法的高效率。最终每一个有效的算法搜索结果所生成的矩阵都可以被转换回满足刚性可折叠性的山谷线分布。

图3 算法设计

图4 算法伪代码

        此外，通过判断矩阵的对称性，还可以去除大量山谷线重复的构型，如图5中double corrugated折纸图案的山谷线重构分析所示。所提出算法的高效性与准确性通过大量的可视化图形和物理模型得到了验证。

图5 Double corrugated折纸图案的山谷线重构分析结果

        所提出的方法可以从2D折纸镶嵌进步一推广到形状更复杂、构型更丰富的3D折纸结构。以图6中的3x3x3镶嵌为例，研究发现它竟然存在6642种满足刚性可折叠性的山谷线分布方案。在此过程中，发现折纸图案的山谷线重构会引起泊松比的显著变化。当折纸图案满足图5所示的3种典型山谷线分布方案时，分别表现出面内的负、零和正泊松比，这一结果通过运动学模型和DIC实验得到了定性、定量验证。

图6 3D折纸镶嵌的典型构型与变形模式

        综上所述，本研究提出了一种结合机构运动协调条件与图形表达的高效算法，可以精准辨识四折痕折纸及其镶嵌的山谷线重构并去除重复构型，为基于山谷线重构原理的的多功能结构设计提供了理论基础与技术支撑。

Liu W, Cao S, Chen Y*. Mountain-valley crease reconfiguration of 4-crease origami vertices and tessellations. International Journal of Mechanical Sciences, 2024, 273, 109224.
(https://doi.org/10.1016/j.ijmecsci.2024.109224)