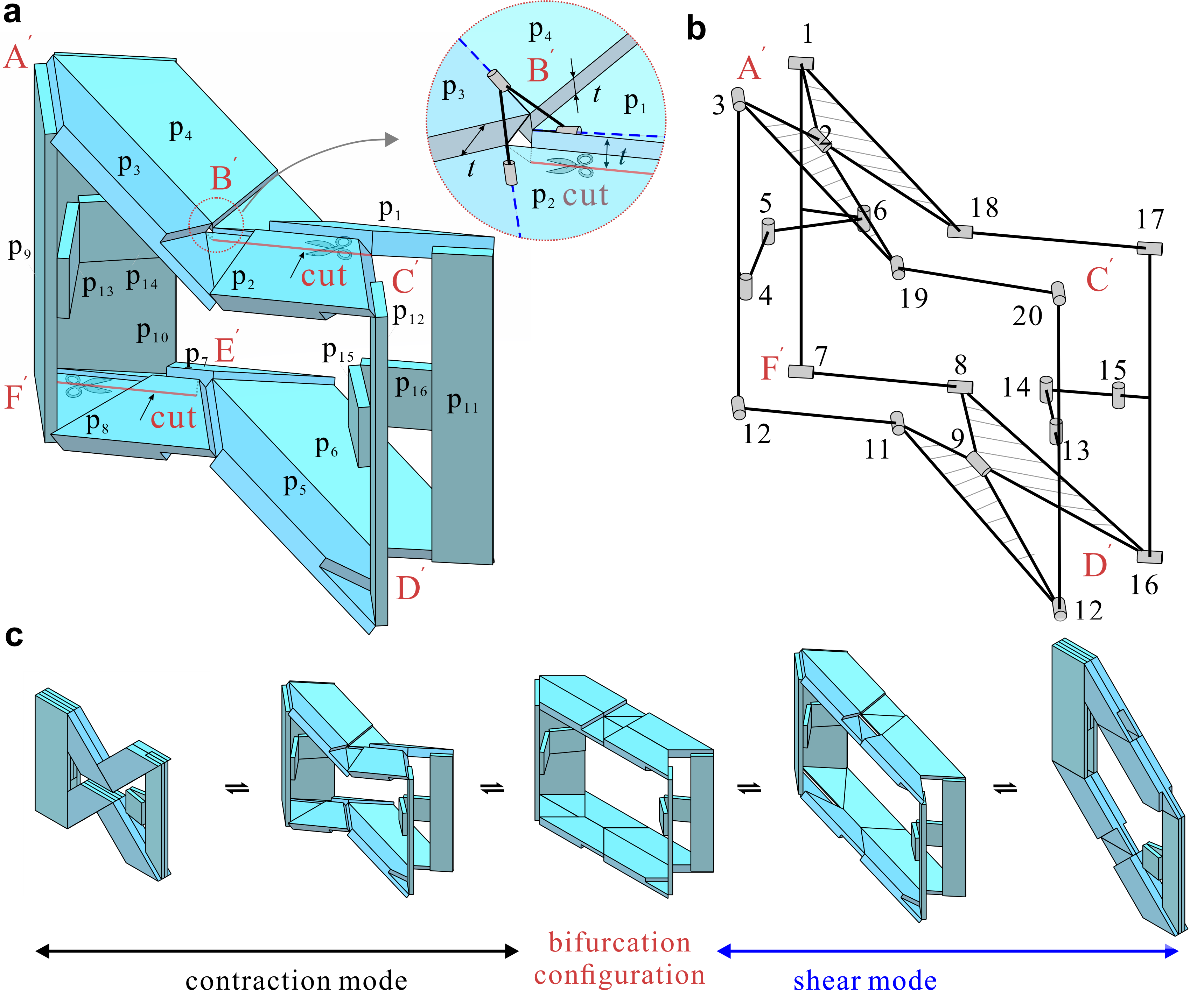
基于机构运动分叉的折痕山谷线转换、折痕激活与休眠是设计具有多形状变化能力的可重构折纸结构的重要方法。然而，由于分叉点位置的运动路径存在不确定性，使得单自由度折纸结构在单一电机驱动下难以实现指定的运动路径重构。为解决这一问题，天津大学机械工程学院陈焱教授团队将厚板理论与剪纸技术相结合，应用于具有多条分叉路径的管状折纸结构，设计出了能够在指定构型之间实现重构的厚板折纸结构，并成功研制样机开展测试验证。结果表明，通过单一电机就能实现厚板管状折纸在收缩和剪切两种运动模式之间快速的重构控制。
        研究团队首先从经典零厚度四折痕管状折纸出发，通过运动学分析确定单个管状折纸结构存在三条运动路径且共用一个分叉点。如图1所示，管状折纸运动通过分叉点vii后，能够到达包括收缩运动模式下的构型i-iv和剪切运动模式下的构型v-vi在内的六种构型。

图1 零厚度管状折纸的运动分叉

        虽然零厚度管状折纸是单自由度的，理论上单一电机驱动其中一个关节即可实现运动控制，但由于相似运动构型的存在，折纸在通过运动分叉点时难以实现从其中一个收缩运动模式（如i）到剪切运动模式（如v）的切换。为此，研究团队先利用传统的厚板转化方法，将零厚度折纸中Miura顶点对应的球面四杆机构转化为空间过约束Bennett 4R机构，同时将相邻的两个Eggbox顶点转化为 Bricard 6R机构，实现了管状折纸的厚板化。虽然厚板管状折纸与原始折纸结构具有运动等价性，但由于Bennett 4R机构的存在，使得管状厚板折纸结构失去了可重构性，如图2所示。

图2 不可重构的厚板折纸管状结构

         随后，团队在Bennett 4R机构对应的位置（B'，E'）引入了剪痕，如图3所示，并在两侧添加了四块面板（p₁₃-p₁₆）。此改进使得厚板折纸管形成了6R-8R-6R-8R机构的装配体，不仅保留了零厚度折纸的单自由度运动特点，还具备了仅在目标构型（i）和（v）之间重构的能力。

图3 具有可重构性的厚板管状折纸结构

        如图4和视频1所示，团队制作了厚板管状折纸结构的铝合金样机模型，并通过单一电机驱动实现厚板管状折纸结构在收缩、剪切两种运动模式之间快速、准确的切换。研究发现，除了在目标构型（i）和（v）之间进行重构外，通过选择性地布置剪痕和驱动位置，还可以实现任意收缩运动模式下的构型（i-iv）到剪切运动模式下的构型(v-vi)之间的重构。

图4 单一驱动下的可重构厚板管状折纸结构样机

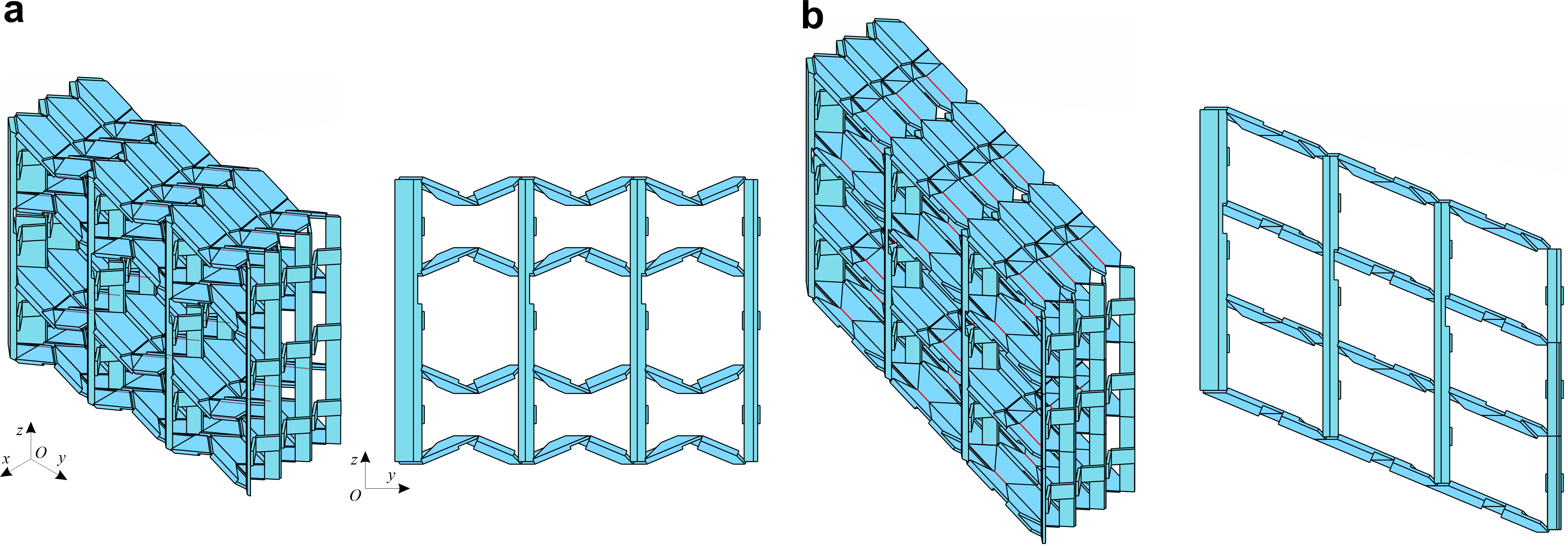
视频1 单一驱动下的可重构厚板管状折纸结构样机

        此外，该类型可重构厚板管状折纸结构可以在三维空间组合形成大型可重构结构，如图5所示。

图5 可重构管状厚板折纸的三维空间组合

        上述研究论文近期发表于ASME Journal of Mechanisms and Robotics期刊。论文的共同通讯作者为天津大学陈焱教授与张霄副研究员，第一作者为天津大学博士生刘伟奇，第二作者为天津大学硕士生宋宇星。本研究所提出的可重构厚板管状折纸结构可实现单一驱动下的目标构型快速切换，不仅可以应用于可重构天线、变形翼等具有多功能需求的场景，同时也为如何通过机构设计降低可重构系统的控制复杂性提供了思路。

Liu W, Song Y, Chen Y*, Zhang X*. Reconfigurable thick-panel structures based on a stacked origami tube. Journal of Mechanisms and Robotics, 2024, 16(12): 121005.
(https://doi.org/10.1115/1.4064836)