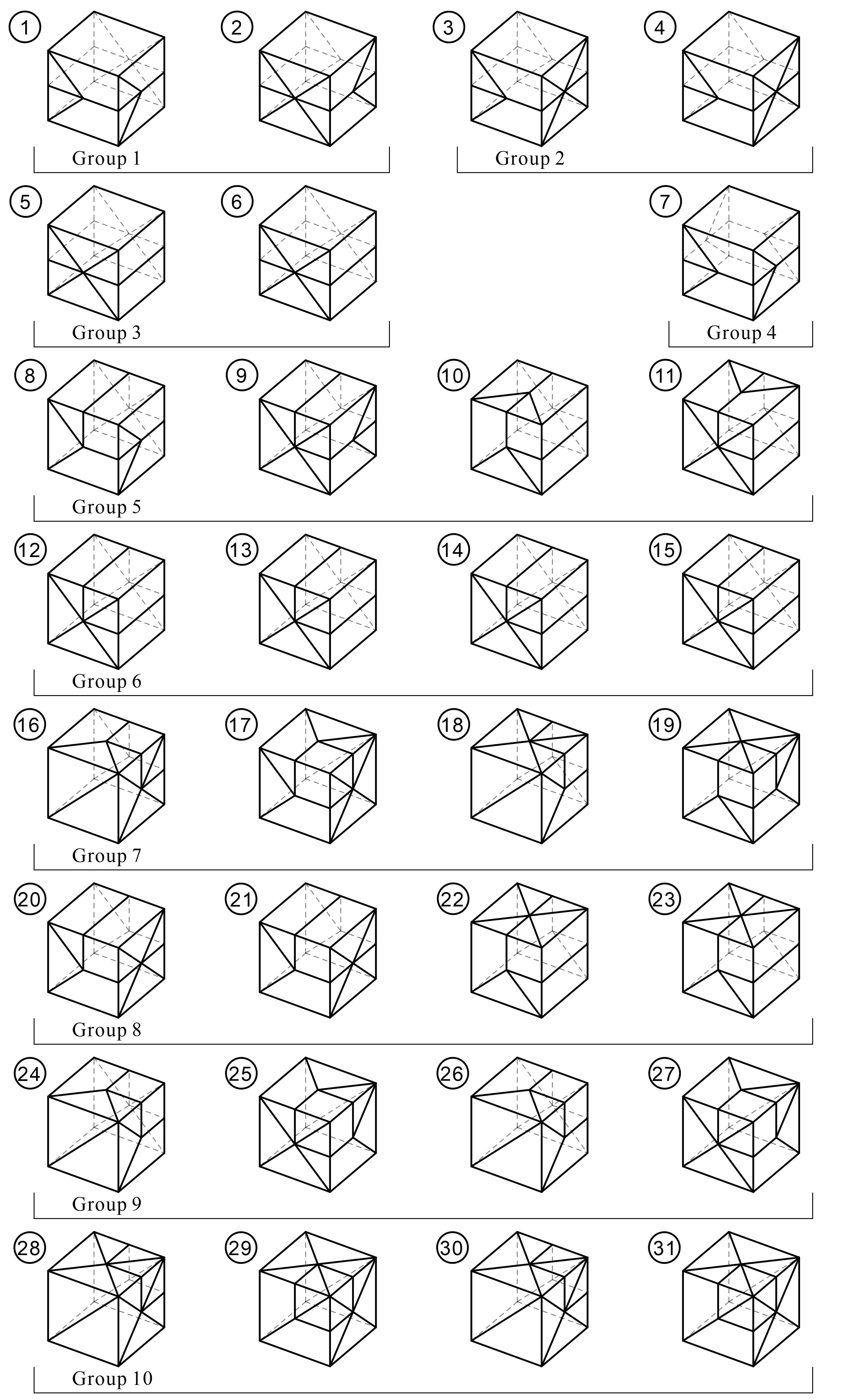
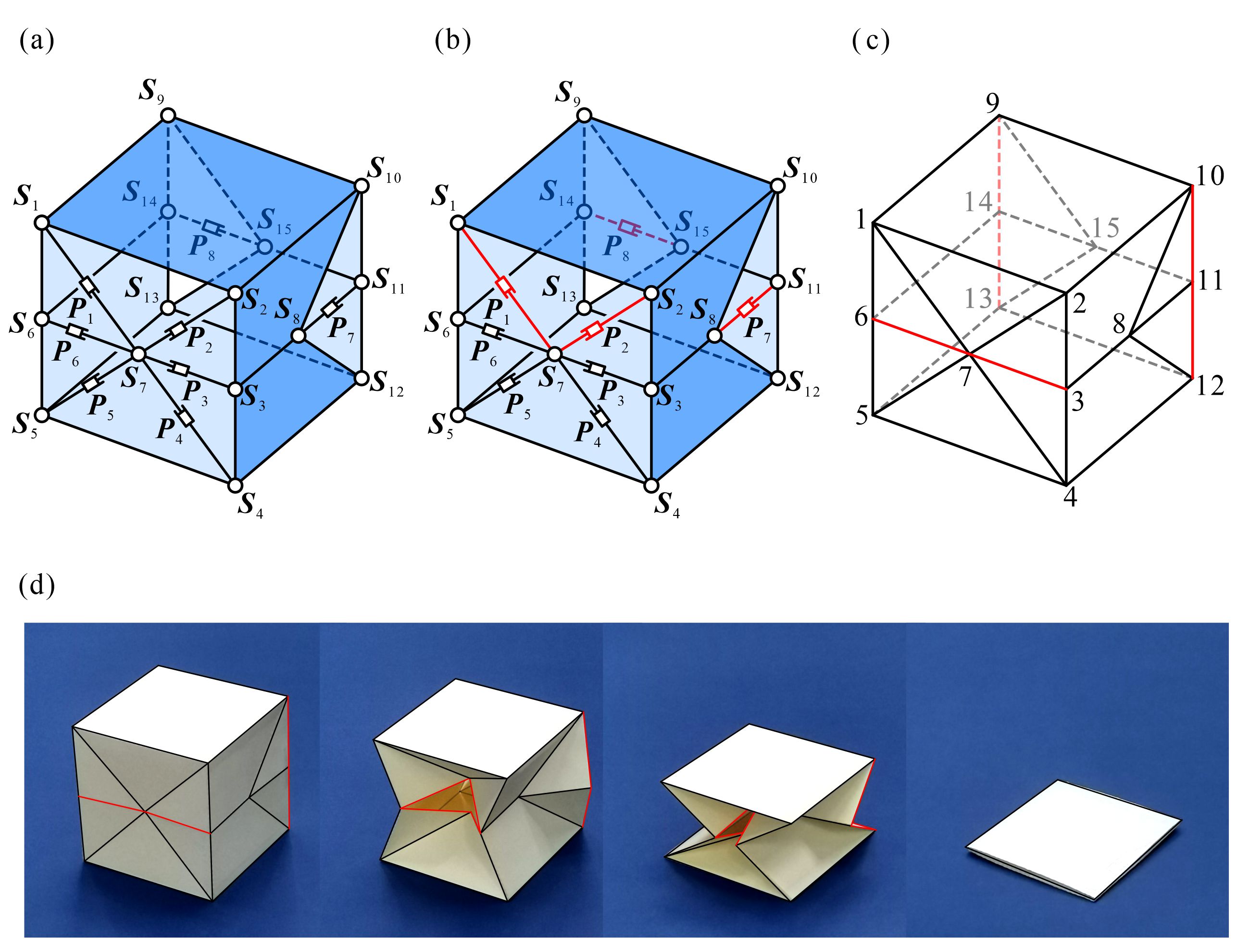
折纸多面体结构可通过合理设计折痕与剪痕实现多面体变换和大折展比运动，在超材料和可展结构等领域具有广阔的应用前景，例如机械、声学、电磁超材料以及可展开天线、电池阵、居住舱等。立方体因具有对称性好和易于拓展等优势拥有巨大应用潜力，为了实现工程应用所需的展开封闭、大折展比和易于折展等特性，需要设计出少剪痕、少自由度的刚性可平折立方体。现有的多面体折痕与剪痕设计方法大多依赖于经验或枚举，难以设计出满足要求的折纸多面体，因此，亟需提出系统的折痕和剪痕设计方法。
        近日，天津大学机械工程学院陈焱教授团队与上海宇航系统工程研究所李明高级工程师合作，以折纸立方体为研究对象，提出了系统的折痕和剪痕设计方法，实现了立方体的刚性平折；提出利用弹性膜密封剪痕构造双稳态立方体的方法，并通过参数化分析实现了能量峰值的定制化设计。
        刚性可平折剪纸立方体的折痕设计采用3D直骨架方法。通过设计共获得如图1所示的31个立方体折痕图案，考虑旋转和镜像对称性，其中共有10组不同的折痕图案。

图1 基于3D直骨架方法的立方体折痕图案。

        根据bellows定理，封闭多面体是不可刚性折叠的，因此必须在基于直骨架方法设计的立方体折痕图案表面引入剪痕。为设计少自由度与少剪痕折叠方案，研究者提出一种新颖的剪痕设计方法：以图1中的立方体2为例，首先基于剪痕与移动副的等价性将部分折痕转化为移动副，得到折纸立方体的等效机构（图2a）；然后利用机构学理论建立机构自由度与可动移动副之间的关系方程，从而建立机构自由度与剪痕的关系。利用该关系方程可在给定自由度数目条件下直接确定可行的剪痕排布方案而不用进行枚举。对于立方体2，在单自由度运动条件下的一种可动移动副方案如图2b所示（其中红色移动副可动，黑色移动副固定不动），图2c是从可动移动副转化而来的一种剪痕（红色）方案，相应的折纸模型如图2d所示。

图2 剪痕设计方法及其应用。(a) 从立方体2转化得到的等效机构；(b) 一种单自由度的可动移动副方案（其中红色移动副可动，黑色移动副固定不动）；(c) 从可动移动副转化而来的一种剪痕（红色）方案；(d) 折纸模型。

        在完全展开和完全折叠构型下，利用前述方法设计的剪纸立方体表面的剪痕是闭合的，而在折叠过程中，剪痕是张开的。如图3a所示，研究者基于此特点提出了利用弹性膜（黄色）密封剪痕构造双稳态立方体的方法，并利用超弹性理论模型求解出膜的能量峰值随几何参数的变化规律以及双稳态参数设计区域（图3b），结果表明双稳态结构的能量峰值可通过改变几何参数进行定制化设计。选取一组双稳态设计参数制造了相应的实物模型，并通过理论与实验验证了其双稳态特性，如图3c和3d所示。

图3 双稳态立方体的几何参数、理论分析及实验结果。(a) 几何参数；(b) 能量峰值随几何参数变化的云图；(c) 实验和理论的力-折叠率曲线；(d) 实验和理论的能量-折叠率曲线。

        上述研究的论文于2024年7月28日在线发表于International Journal of Mechanical Sciences期刊。论文的通讯作者为天津大学陈焱教授，第一作者为天津大学博士生张悦豪。该研究基于剪痕与移动副的等价性提出了一种不依赖于枚举的剪痕设计方法并成功应用于刚性可平折立方体的设计中，此外还利用剪纸立方体构造出能量峰值可定制设计的双稳态结构。研究成果丰富了剪纸结构的设计理论，所提出的双稳态立方体在可展开居住舱、可编程机械超材料等领域具有良好的工程应用前景。

Zhang Y#, Zhang X#, Li M, Chen Y*. The rigid and flat-foldable kirigami cubes. International Journal of Mechanical Sciences, 2024, 282: 109605.
(https://doi.org/10.1016/j.ijmecsci.2024.109605)