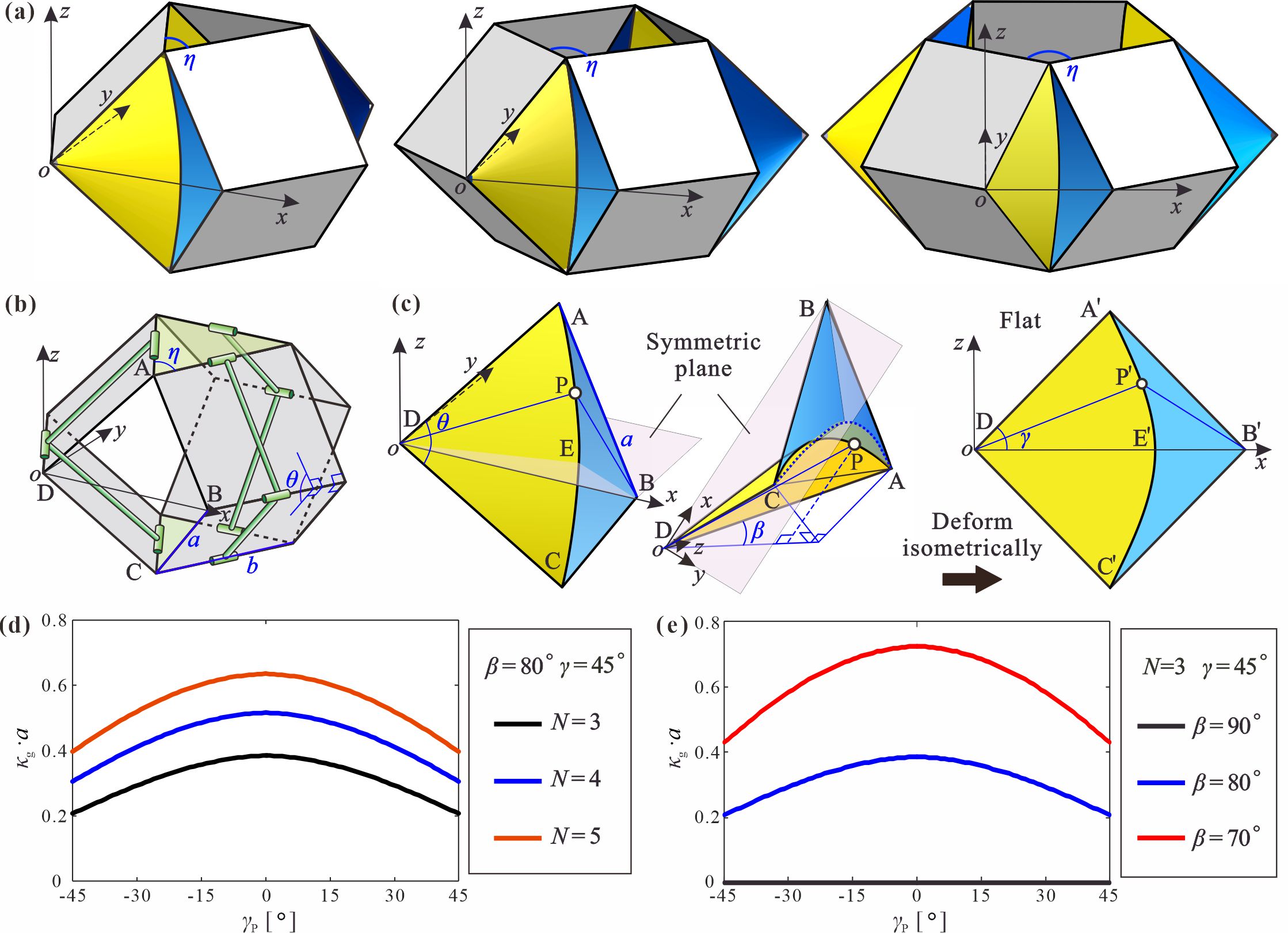
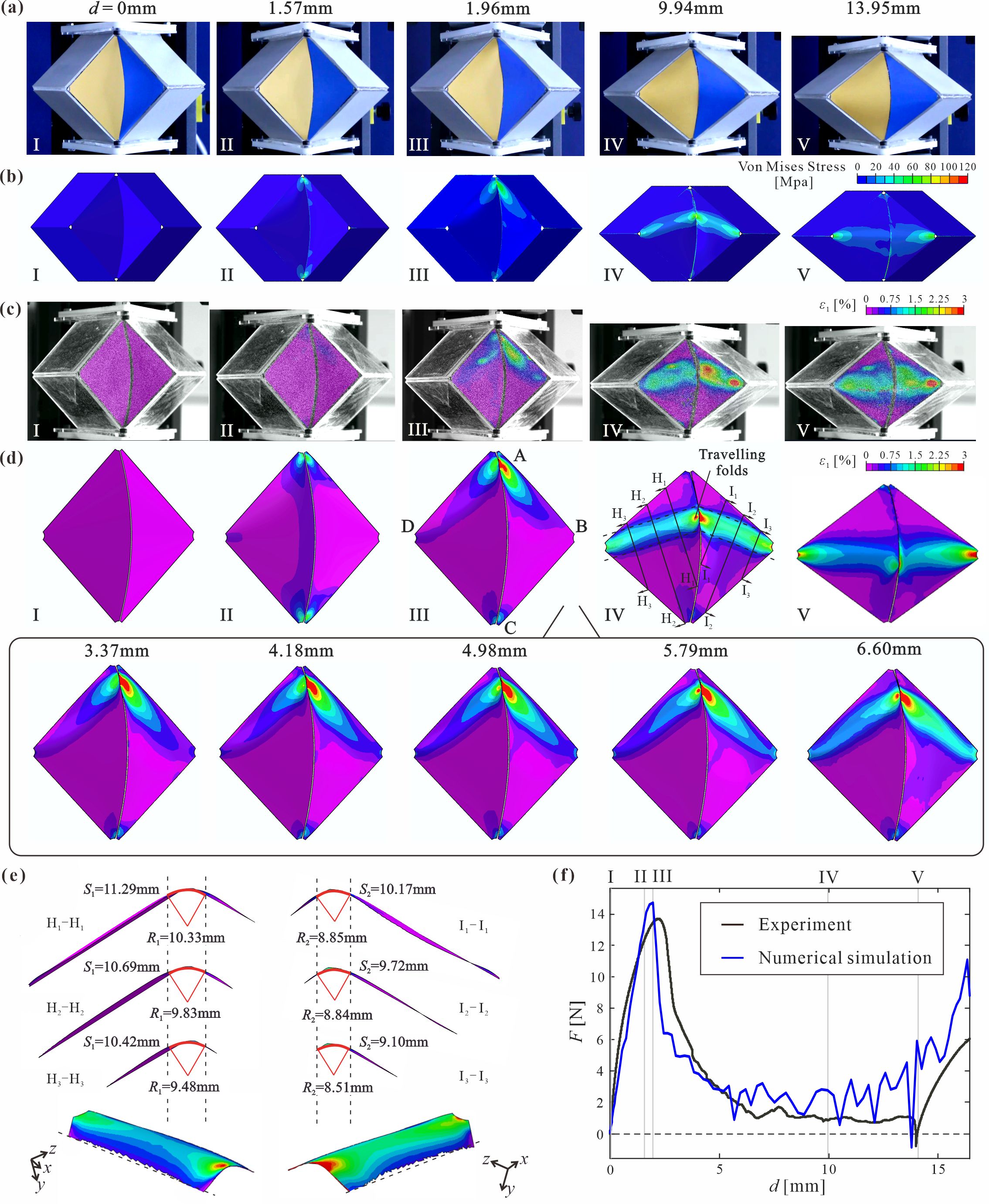
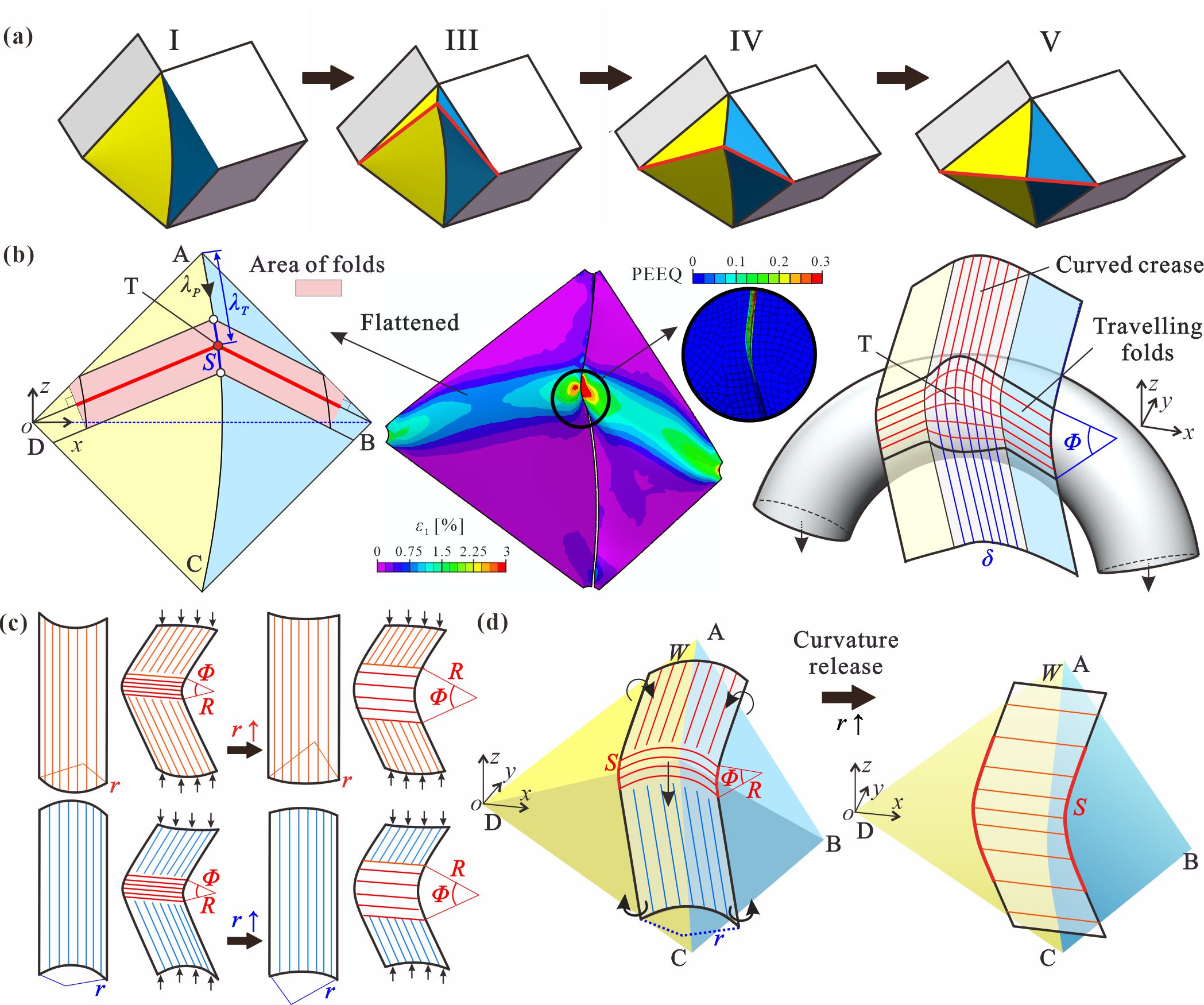
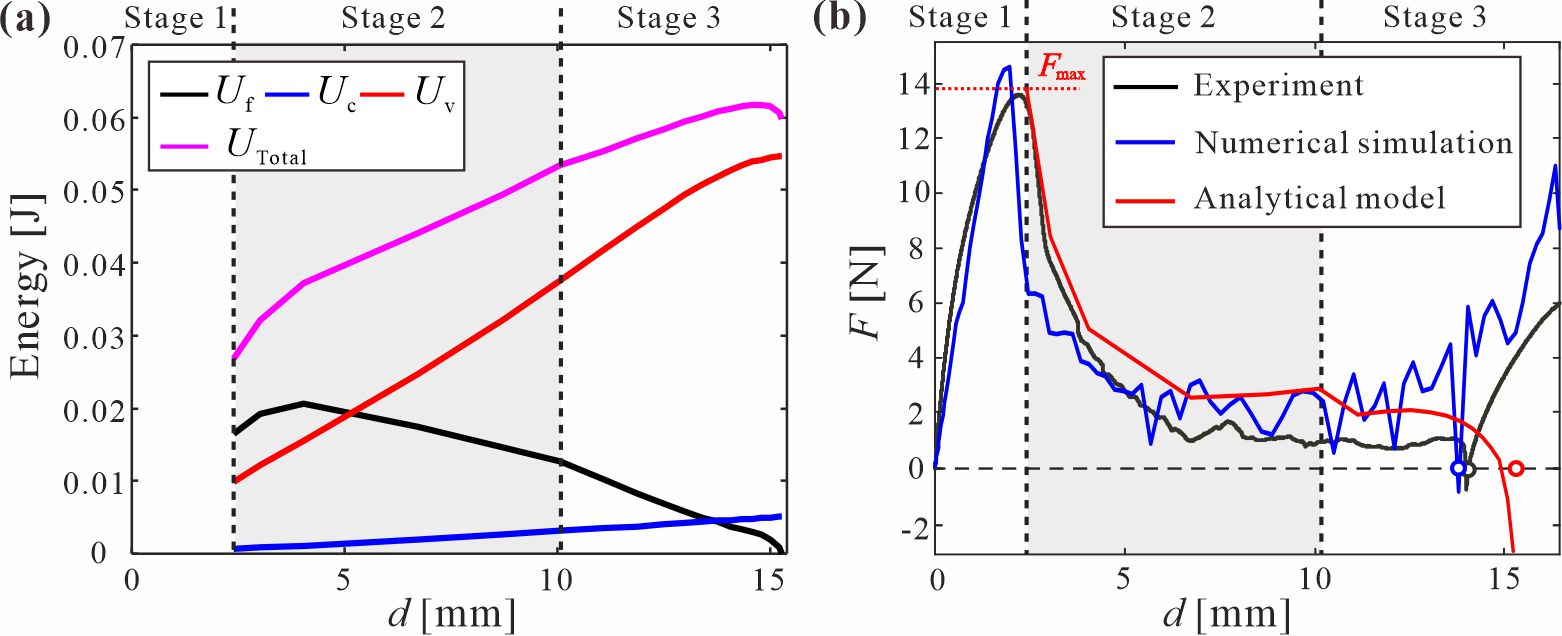
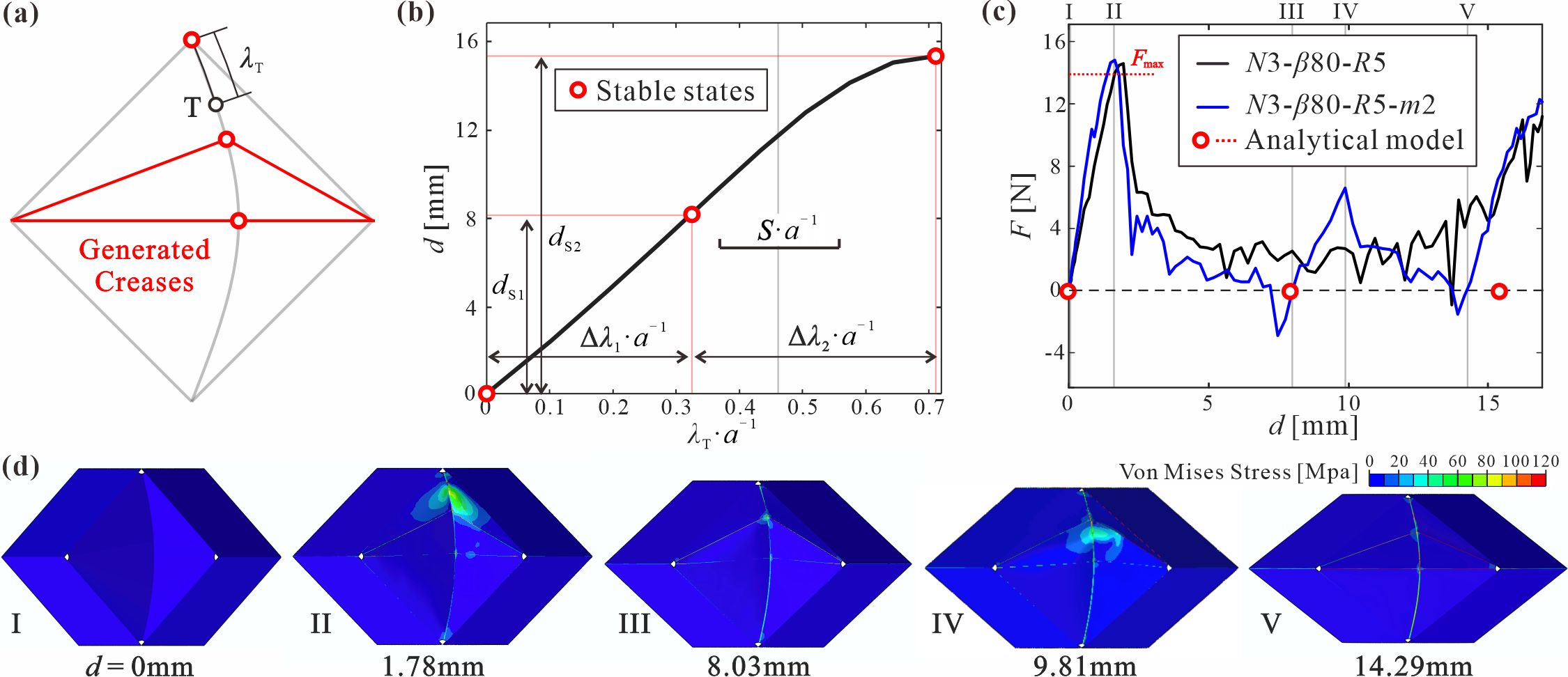
导读

        多稳态结构能够实现不同稳定构型之间的快速切换，在能量吸收、机器人、机械计算和存储等领域应用广泛。作为一种典型的非刚性折纸，曲纹折纸在折叠过程中同时存在折痕转动与面板变形，为多稳态结构的设计提供了一种新思路。然而，现有曲纹折纸结构主要是在自由边界条件下发生变形，这使其变形过程遵循于母线的弯曲模式，进而表现出与曲面形成过程相同的能量单调性。因此，曲纹折纸结构主要通过面板的弹性弯曲、恢复和反向弯曲变形来实现最多两个稳定双稳态。

        为此，天津大学马家耀教授团队设计了一系列由平面与曲面面板构成的曲纹折纸结构。在平面面板所形成的Sarrus机构的边界约束下，曲面面板不再遵循基于母线的弯曲模式，而是产生了类比于塑形力学中移行塑性铰的移行弹性铰。基于这一变形机制建立了曲纹折纸结构单轴压缩的解析模型，并通过将移动过程中特定位置的弹性铰链转化为物理折痕，在单一结构中实现了可编程的多稳态特性。这一成果以“Programmable Multi-Stability of Curved-Crease Origami Structures with Travelling Folds”为题发表于固体力学旗舰期刊Journal of the Mechanics and Physics of Solids。天津大学机械工程学院博士研究生柴思博为论文第一作者，马家耀教授为通讯作者。论文合作者还包括北京理工大学宇航学院博士后胡洲、天津大学机械工程学院陈焱教授以及牛津大学工程科学系由衷教授。该研究受到了国家自然科学基金与科学探索奖的资助。
        研究团队首先提出了一种通过约束边界引导曲纹折纸成型的设计方法，构建了一系列具有不同截面形状的曲纹折纸结构。这些结构由多个平面和曲面面板组成（图1a）。其中，平面面板形成了一个Sarrus机构，限制了初始构型中曲面母线的分布（图1b）。曲面面板由两个锥面构成，并通过一条空间曲线折痕连接（图1c）。通过折叠运动学分析，建立了平面与曲面面板在几何匹配条件下的几何构型。在此基础上，截面边数、锥面半锥角等独立几何参数可以调控平面折叠角、曲面方程及折痕曲率分布（图1d和e）。

图1 曲纹折纸结构的几何设计

        通过实验与数值仿真方法，探究了曲纹折纸单元在单轴压缩加载下所形成的移行弹性铰的变形模式。研究结果表明，在Sarrus机构边界的引导下，曲面面板经过对称的弹性屈曲变形，逐渐形成一对非对称的弹性铰链。这对铰链表现为连接圆锥顶点并相交于曲线折痕的高局部应力条带，同时具有近似圆柱面的弯曲变形（图2）。铰链在顶部端点附近产生，并随着加载向曲面中间移动，同时反力先降低后逐渐平坦。当两个弹性铰接近水平时，会突然释放弯曲曲率，快速变形并到达第二个稳定状态。根据结构的变形和加载曲线形式，变形过程被划分为移行弹性铰的生成、传播和释放三个阶段。

图2 曲纹折纸结构的变形过程

        进一步建立了移行弹性铰的解析模型。首先通过构建等效离散几何，从几何协调性的角度阐明了铰链移动的变形机理（图3a）。在此基础上，引入了三种变形机制：弹性铰的圆柱面弯曲、铰链相交处的顶点拉伸和曲率释放阶段的等效带状弹簧变形（图3b-d）。根据这些变形机制，计算了压缩过程中存在的三种能量形式：铰链弯曲的弹性应变能、折痕折叠的弹性应变能以及顶点拉伸的塑性能量（图4a）。解析模型的结果表征了力-位移曲线的整体趋势，同时预测了初始峰值力和第二个稳态的加载位置（图4b）。

图3 移行弹性铰、顶点拉伸与等效带状弹簧的变形机制

图4 能量与反力的解析结果

        在上述移行弹性铰变形机制的基础上，如果将铰链移动过程中扫过的曲面母线转化为物理折痕，当弹性铰到达这些折痕时，结构的应变能将显著降低，从而形成额外的稳定状态。基于这种折痕转化方法，设计出具有两处折痕转换的三稳态单元（图5a），其稳态数量与加载距离可以通过调节折痕转化的数量和位置进行编程（图5b和5c）。此外，引入的折痕不会影响结构的初始屈曲变形（图5d），因此解析模型仍能准确预测多稳态结构的初始峰值力。

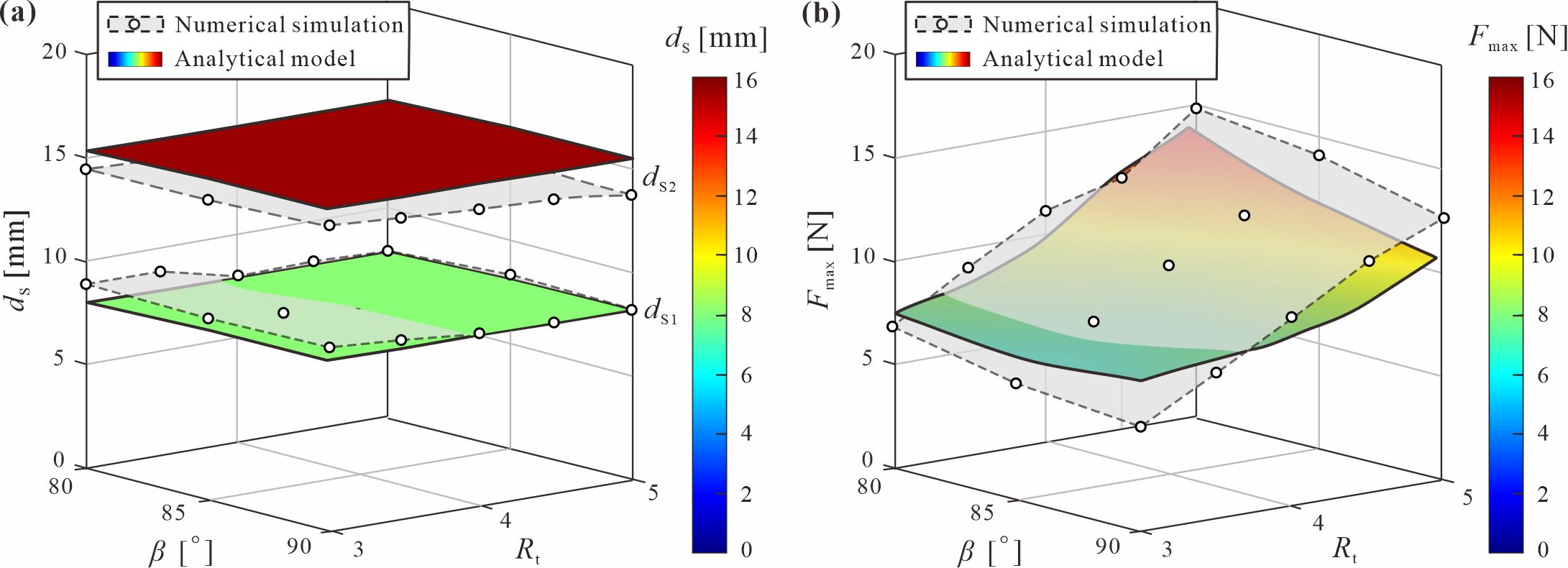
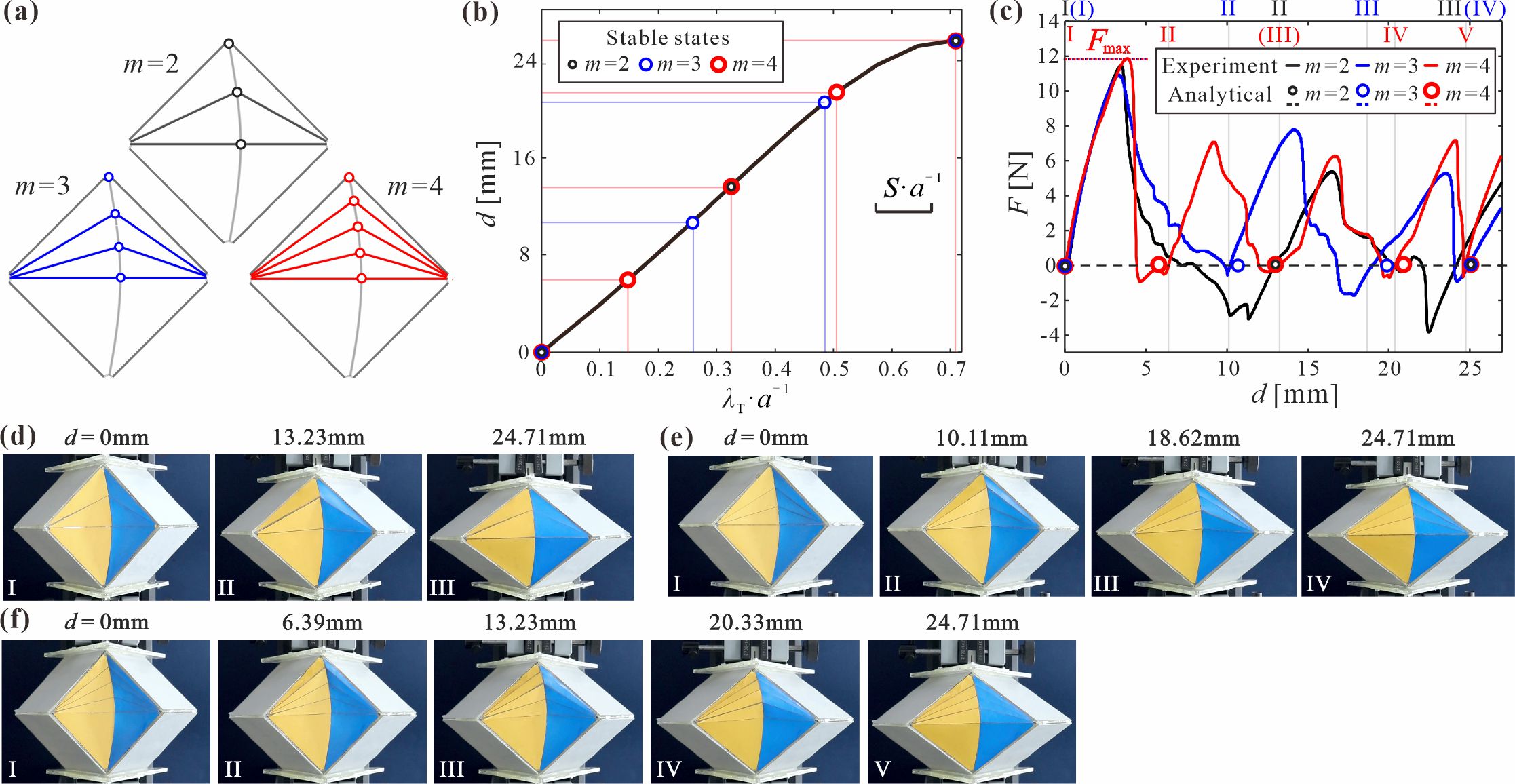
图5 折痕转换方法与多稳态的构建

        进一步探究了折痕曲率参数以及面板与折痕的厚度比对相邻稳态距离和初始峰值力的影响。解析模型和数值仿真结果表明，稳态位置几乎与几何参数无关，而增大折痕初始曲率或增加厚度比则会显著提升初始峰值力（图6）。因此，与现有研究中多稳态单元通常只能在最多两个变量（如稳态数量与初始峰值力或稳态位置与能量势垒）上实现可编程不同，本研究所提出的曲纹折纸单元具备对稳态数量、位置及初始峰值力的全面编程能力。通过对设计得到的具有三、四和五个稳态的折纸单元进行压缩实验，这种全面编程能力得到了进一步验证（图7）。

图6 基于几何参数的多稳态性能编程

图7 可编程多稳态特性的实验验证

        综上所述，本研究提出了一系列由约束边界引导的曲纹折纸结构，展现出移行弹性铰的生成、传播和释放的独特变形机制。基于解析模型和折痕转换方法，实现了曲纹折纸单元的多稳态特性，以及稳态数量、位置以及初始峰值力的全面编程，为开发具有可编程机械性能的通用多稳态结构开辟了一条新途径。

Chai S, Hu Z, Chen Y, You Z, Ma J*. Programmable multi-stability of curved-crease origami structures with travelling folds. Journal of the Mechanics and Physics of Solids, 2024, 193, 105877.
(https://doi.org/10.1016/j.jmps.2024.105877)