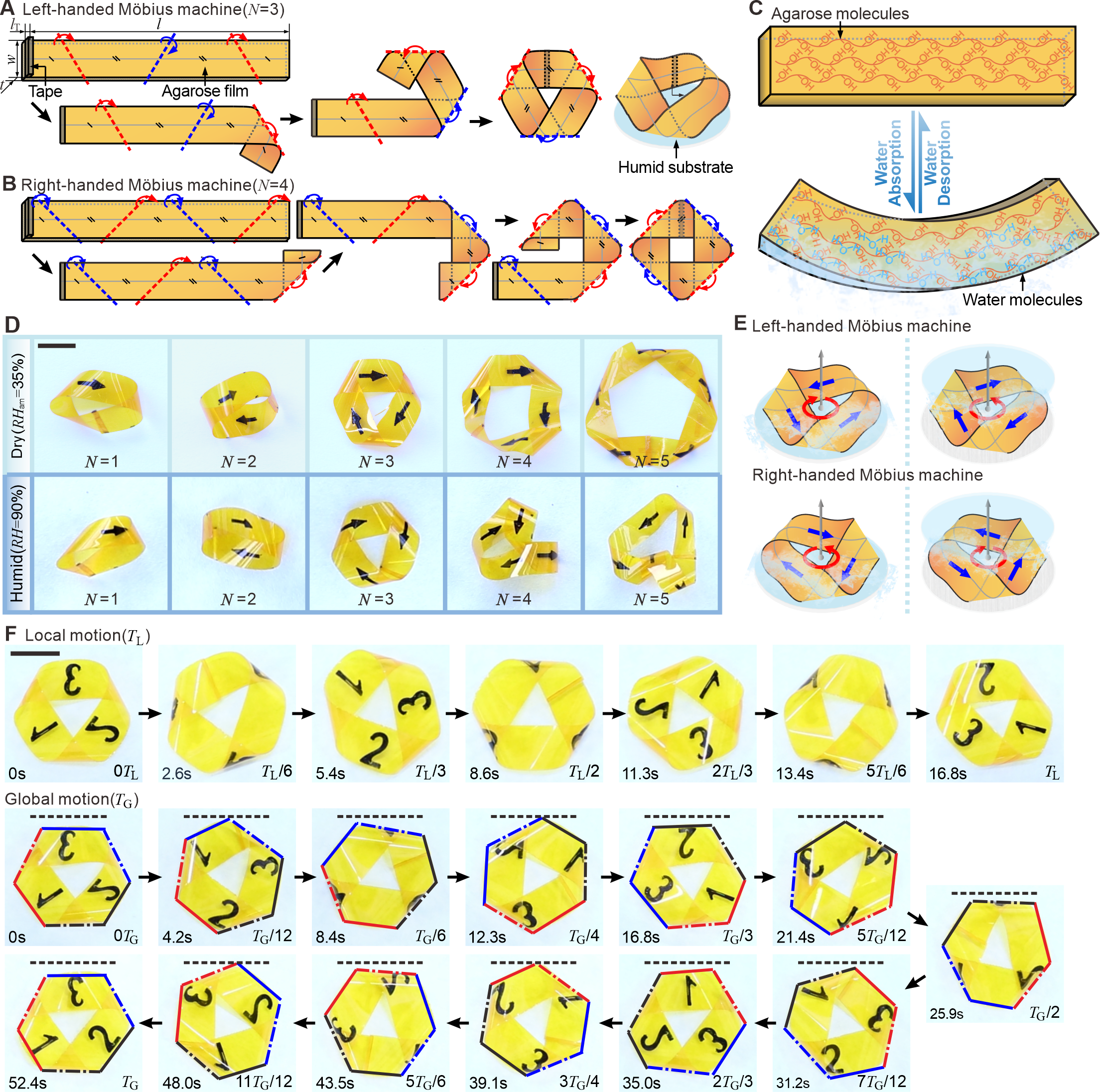
导读

        利用刺激响应材料制造的软体机械系统能够在光、温度、电、磁场等外界环境的作用下实现可编程的多模态变形。然而，此类系统的持续形态变化及运动往往依赖于外界刺激的实时精准调控，这极大限制了其在智能机器人系统，人机交互等领域的潜在应用。要使这类机器人在恒定的外部刺激下实现持久的自持运动，解决几何设计、物理建模和参数优化在内的诸多挑战尤为重要。

        近日，天津大学机械工程学院陈焱教授团队联合天津大学化工学院张雷教授团队，西湖大学工学院吕久安教授团队，基于莫比乌斯(Möbius)带的拓扑结构，开发出一类可在恒定的环境中持续运行的三重对称莫比乌斯机器人。结合可展曲面与扩散理论而构建的物理模型，揭示了其在湿度梯度下的形状保持和持续运动机制。实验证明，该机器人可实现超252小时的自主周期性运动并持续输出机械功，并对环境湿度进行动态感知。成果于2025年2月9日在线发表于国际权威期刊《先进功能材料》(Advanced Functional Materials)。论文共同通讯作者为天津大学陈焱教授、天津大学张雷教授，共同第一作者为天津大学博士生杨晓辰、南开大学赵维强副教授，天津大学马家耀教授。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

        在本研究中，结构设计是实现湿度驱动莫比乌斯机器人功能的关键。研究人员充分利用琼脂糖薄膜的亲水羟基特性，使其在吸水膨胀时快速弯曲，失水时迅速恢复平整。通过精准控制琼脂糖膜的折叠次数为三次，将其首尾相连形成三重对称的莫比乌斯结构，有效避免了一重和二重模型因接触不稳而无法持续运动，以及四重和五重模型因预应力不足而出现局部褶皱的问题。这种优化的结构设计使莫比乌斯机器人在湿度驱动下展现出两种独特的周期性运动模式：一方面，材料沿条带路径周期性地弯曲和伸直，适应各处的曲率变化，呈现出类似传送带的局部自转运动；另一方面，从整体观察，莫比乌斯机器人的六边形轮廓绕其中心轴旋转，实现全局公转运动（视频2）。

图1. 由湿度敏感的琼脂(AG)薄膜制成的莫比乌斯机器人。

视频1. 莫比乌斯机器人的制造过程。

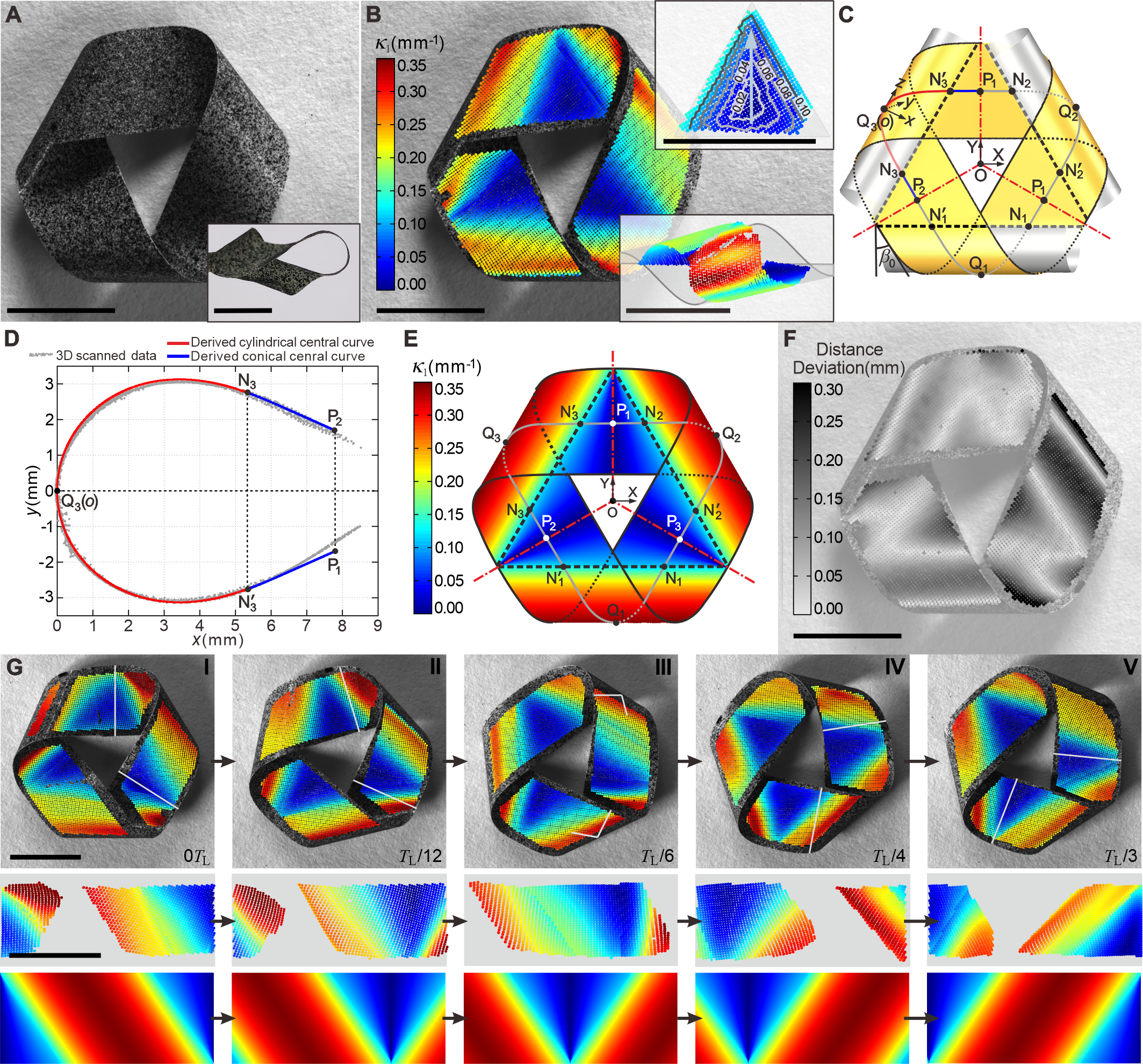
视频2. 莫比乌斯机器人的局部和全局运动。

        研究者之后利用扫描技术对静止状态下的机器人几何形状进行重建(图2）。根据其主曲率分布情况以及不可拉伸的可展曲面理论，整个闭环结构得以简化为三个相同的沿银色圆柱体缠绕的柱面，并通过三个近乎平坦的梯形锥面相互连接。进一步，利用二次曲线拟合柱面和特定曲线拟合锥面，从而获得机器的完整几何形状，与扫描结果相互吻合。此外，通过比较其在运动和静止状态下的几何形状，他们发现机器人在运动过程中整体形状和曲率分布得以保持，并形成了零弹性能量模式(ZEEMs)，这为机器人的自主运动奠定了基础。

图2. 莫比乌斯机器人的几何建模。

        利用上述几何模型，研究者采用能量分析方法来探讨机器人在运动中化学能与机械能（包括应变能、动能和重力势能）之间的转换关系。鉴于机器人在运动中始终保形，即所有材料必须沿条带的长度方向匀速率移动。进一步依据ZEEMs假设，莫比乌斯机器人在自持运动中吸收与释放的湿度能量始终守恒。结合湿度扩散理论和可展曲面理论，研究者从数学上揭示了莫比乌斯局部运动由曲率变化驱动的潜在运动机制，阐释了机器人稳定局部运动的根本原因。对于整体运动，通过分析滑动摩擦力揭示了其作用机制。局部运动引起的接触点的滚动摩擦力，其切向分力提供了使机器人加速至稳定整体公旋所需的扭矩。此外，该理论模型进一步明确了设计参数与运动速率之间的定量关系，为莫比乌斯机器人在多样化应用场景中的优化设计提供了科学依据（图3）。

图3. 莫比乌斯机器人运动的理论模型。

        为验证理论模型的精确性和可靠性，研究者在不同湿度环境下对不同几何参数的莫比乌斯机器人进行测试（图4）。其最优的自转速度可达25.95r/min远超现有受恒定刺激驱动的软体机器人的最大转速。

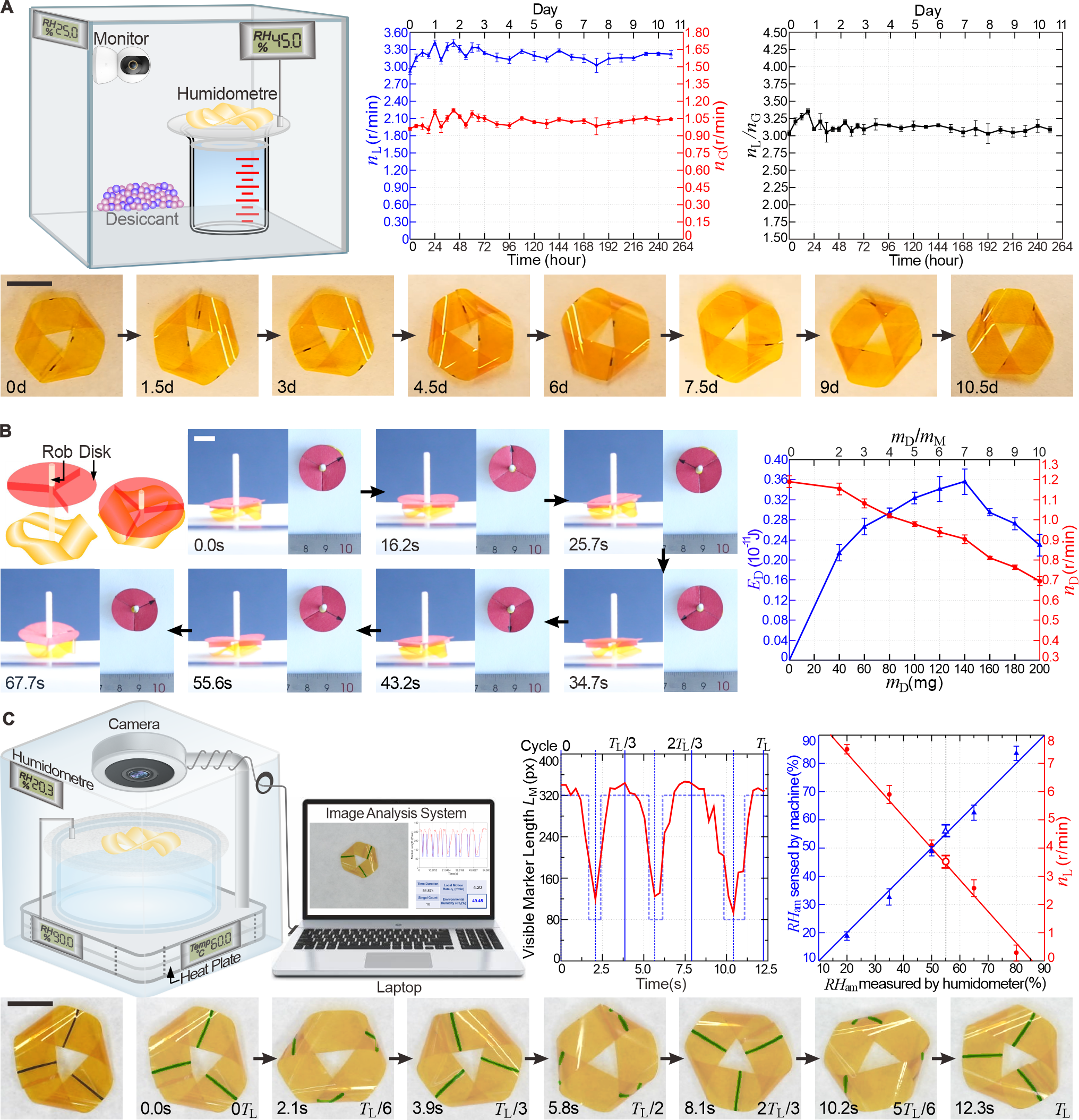
图4. 莫比乌斯机器人运动的参数分析。

        莫比乌斯机器人凭借其独特的结构与性能，在多个应用场景中展现出显著的多功能性和高效性(图5）。在长期运行测试中，该机器人在恒定湿度环境下连续工作252小时(10.5天)，完成超过47500次局部运动周期，充分证明了其卓越的稳定性和自持续能力(视频3）。在机械功输出测试中，莫比乌斯机器人通过公转运动驱动不同重量的纸盘旋转，并持续输出机械能，显示出其在机械功输出方面的良好适应性和可靠性(视频4）。此外，莫比乌斯机器人还具备环境湿度传感功能，借助机器视觉技术，可在2分钟内精准测量相对湿度，与标准湿度计的误差小于5.37%，实现了驱动与传感的双重功能(视频5）。

图5. 莫比乌斯机器人运动的样机演示。

视频3：长期运动演示。

视频4：机械功输出演示。

视频5：环境湿度计演示。

        综上所述，本研究提出了一种基于湿度响应的三重莫比乌斯机器人，其可在湿度刺激下，实现稳定且持续的周期性运动。通过耦合扩散理论与可展曲面的数学定义，揭示了曲率驱动运动的内在机制，并建立了结构设计、材料变形与机器人局部及全局运动之间的定量关系，从而实现了基于特定需求的参数化设计。这一理论模型不仅为莫比乌斯机器人的设计提供了坚实基础，更为开发具有独特拓扑结构的新型软体机器人开辟了新路径，使其能够实现由恒定刺激驱动的持久自调节运动，为先进机器人系统中的前沿应用提供了广阔前景。

Yang X#, Zhao W#, Ma J#, Fu L, Liu M, Xu C, Hu Z, Lv J, Chen Y*, Zhang L*, Threefold Möbius Machine. Advanced Functional Materials, 2025, 202420815.
(https://doi.org/10.1002/adfm.202420815)