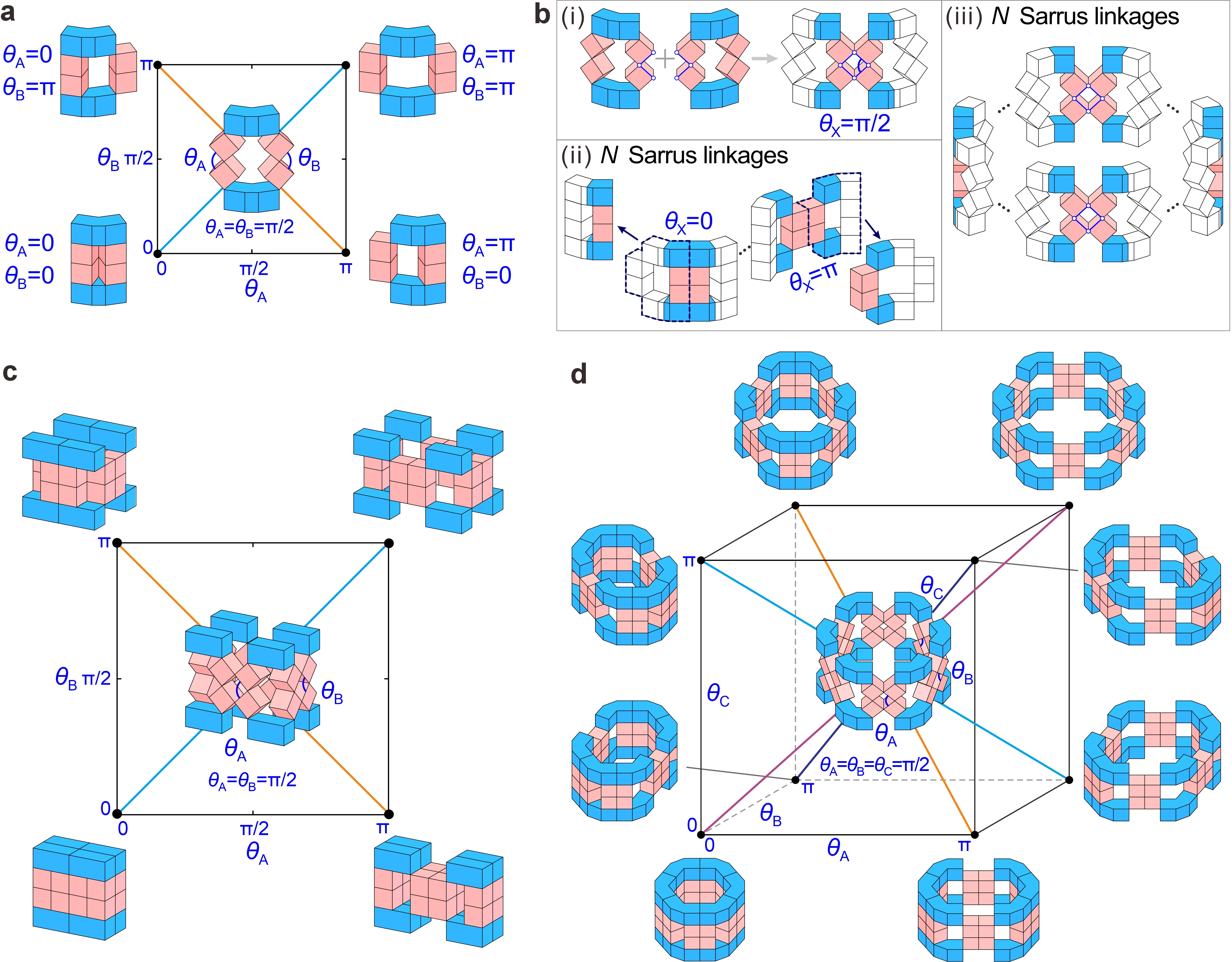
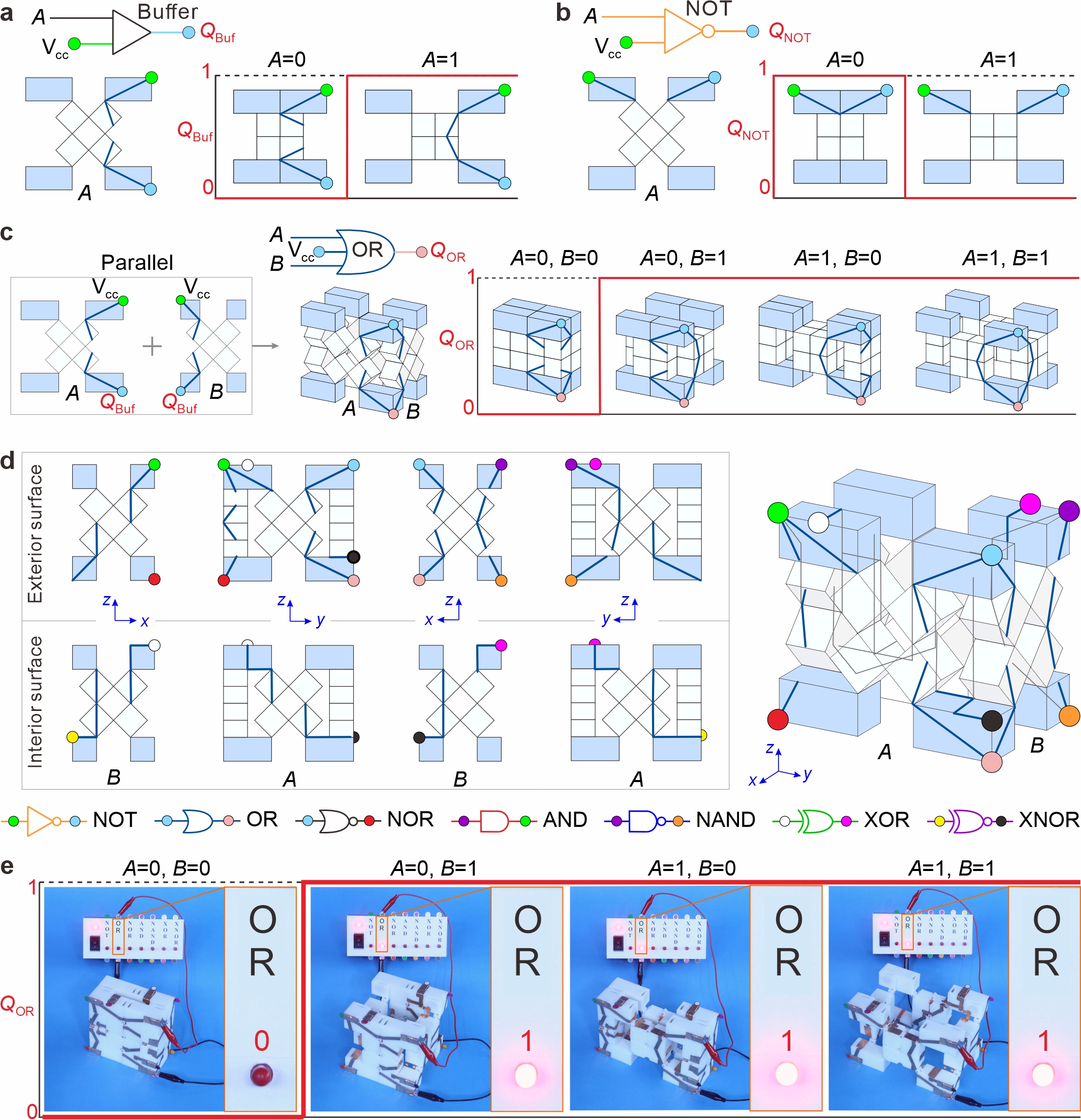
导读

        机械计算超材料借助离散构型间的切换，可在感知外界刺激时自主处理信息，在智能机械系统发展中具有重要意义。然而，当前多数设计基于平面机构或双稳态结构，通常仅提供两种构型，需要大量单元才能实现复杂逻辑运算所需的多输入输出功能，且对系统集成考虑不足。

        为此，天津大学机械工程学院陈焱教授团队联合牛津大学由衷教授和清华大学陈常青教授，提出了一组基于运动分岔的2n边多边形模块，可接收n个独立机械输入，并在2ⁿ种构型间切换。团队首先在四边形模块上实现了所有七个基本逻辑门的集成，并进一步开发了并行乘积和（PCSoP）函数这一最小化布尔函数方法以简化逻辑计算系统。在此基础上，团队在单个多边形模块上实现了包含2位加、减、乘、除运算（首次构建除法器）在内的机械计算、信息显示与识别等逻辑运算功能。相关成果以“A kinematically Bifurcated Metamaterial for Integrated Logic Operation and Computing”为题，于2025年7月17日在线发表于国际综合性期刊《先进科学》(Advanced Science)。论文共同通讯作者为天津大学陈焱教授和张霄副研究员，第一作者为天津大学博士生袭凯莉。硕士生魏靖松为本工作提供了重要的实验支持，马家耀教授、由衷教授和陈常青教授也参与指导了研究工作。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

研究内容

        研究团队从Sarrus连杆（图1a）的运动分岔特性入手，利用4-bar连杆将多个Sarrus连杆连接成闭环超材料（图1b(iii)），从而构建了一种具有单自由度的2n边多边形模块。这些模块能够接收n个独立的机械输入，并通过运动分岔在2ⁿ种极端构型（二面角θ_X=0或π）之间切换。基于此，团队进一步定义了机械位：当θ_X=0时，机械位输入X=0，对应上下蓝色块闭合的构型；当θ_X=π时，X=1，蓝色块分离。例如，图1c中的四边形模块（2n=4）具有两个输入（A, B），可在四种不同的构型（(0, 0)、(0, 1)、(1, 0)和(1, 1)）之间切换。当2n=6时，六边形模块可以接收3个独立输入（A, B, C），并具有8（2³）个极端构型（图1d）；而八边形模块（2n=8）则有 16 个构型。这种设计为二进制机械计算提供了丰富的构型，使得单个模块有望执行复杂的逻辑运算和信息处理任务。

图1 多边形模块的运动分岔行为

        接下来，研究团队将这些多边形模块与电路相结合，构建了用于各种逻辑运算的导电逻辑模块。如图2所示，以四边形模块为例，团队巧妙地在其表面布置电路，实现了缓冲门（Buffer）、非门（NOT）等基本逻辑门的构建，并通过串联或并联Buffer门和/或NOT门依次实现了OR、NOR、AND、NAND、XOR和XNOR门。进一步地，通过共享开关（Buffer和NOT门）和模块表面，成功将所有七个基本逻辑门集成在单一四边形模块上（图2d）。如视频1所示，通过选择性地接通与不同逻辑门相对应的输入和输出节点，集成模块可执行所有七个基本逻辑门。

图2 四边形逻辑模块的设计、集成和实验

视频1 集成了7种基本逻辑门的四边形逻辑模块

        除逻辑门外，多边形模块还能用于执行算术运算等组合逻辑功能。研究团队首先在四边形模块上构建了半加/减法器（视频2）。随后，利用能接收三个独立输入的六边形模块，实现了全加法器的设计（图3a-d，视频3）。得益于团队开发的PCSoP函数，能够在设计过程中对重复的机械逻辑网络组件进行提取并将其简化为单一子任务，显著减少了逻辑运算器所需的开关数量。所设计的全加法器仅需15个开关，相较于基于已有的SSoP函数（需24个开关）和QMSoP函数（需18个开关）的设计，开关数量大幅减少。基于相同的设计思路，团队进一步在八边形模块上实现了2位加、减、乘运算器（乘法器见视频4），并通过引入报错输出Error，首次成功构建了2位除法器（图3e-g，视频5）。这些设计充分展现了基于PCSoP函数开发的多边形逻辑模块在算术运算中的简洁性和高效性。

视频2 基于四边形模块的半加/减法器

图3 基于多边形模块的算术运算

视频3 基于六边形模块的全加法器

视频4 基于八边形模块的2位乘法器

视频5 基于八边形模块的2位除法器

        除机械逻辑与计算外，多边形模块还可用于信息显示与识别等功能（图4）。例如，研究团队利用六边形模块设计了二进制编码十进制（BCD）到LED七段管的显示译码器，能够将3位二进制输入转换为0~7的十进制数，并生成七个输出a~g用于驱动七段LED灯管，从而显示相应的数字（视频6）。此外，团队还利用八边形模块构建了识别模块，可对2~15的二进制数进行解码，并判断其奇偶性、是否为素数以及能否被3整除（视频7）。其他已知输入输出关系的属性也可以通过构建相应的识别模块进行分析。

图4 基于多边形模块的信息显示和识别功能

视频6 基于六边形模块的BCD显示解码器

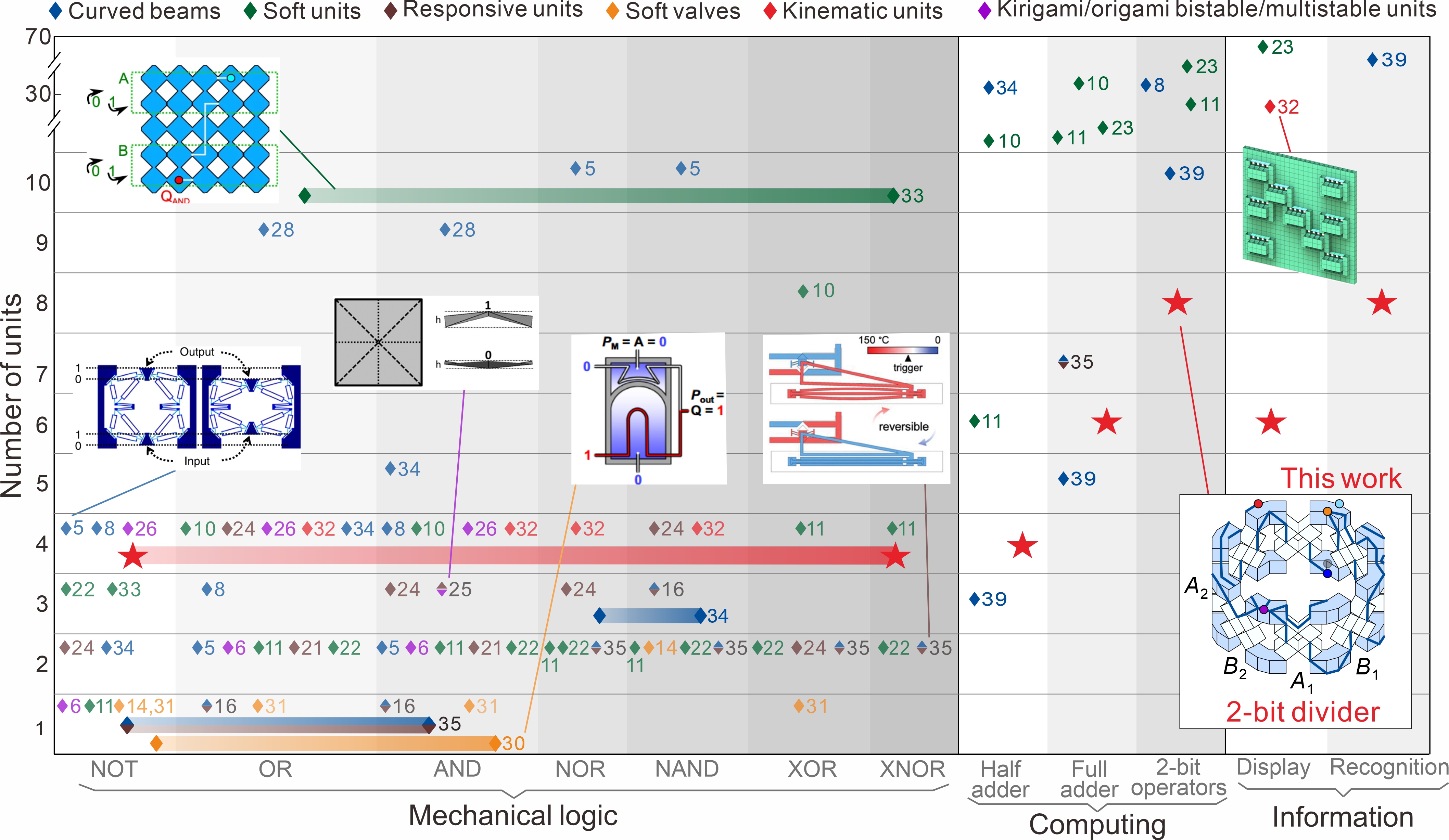
视频7 基于八边形模块的识别模块

        最后，研究团队将本工作与机械逻辑、机械计算、信息显示和信息识别等方面的现有工作进行了比较，如图5所示。结果表明，多边形逻辑模块在实现基本逻辑门和复杂算术运算时，所需单元数量显著减少。例如，本工作仅用一个由4个单元组成的四边形模块就能同时实现所有七个基本逻辑门，所需的单元数量远远少于其他工作。此外，基于多边形模块的逻辑运算也只需更少的单元，就能匹配或超过现有设计的功能。

图5 文本工作与现有研究工作的对比

        综上所述，本研究提出了一种基于运动分岔的多边形模块，通过与逻辑电路耦合，在单个多边形模块上实现了机械计算（包含加、减、乘、除）、信息显示与识别等多种功能，并以所开发的 PCSoP最小化布尔函数显著减少复杂逻辑运算所需开关与单元数量，从而大幅提升了机械计算系统的集成水平。

Kaili Xi, Jingsong Wei, Xiao Zhang*, Jiayao Ma, Zhong You, Changqing Chen, Yan Chen*. A kinematically Bifurcated Metamaterial for Integrated Logic Operation and Computing, Advanced Science, 2025, e09829.
(https://doi.org/10.1002/advs.202509829)