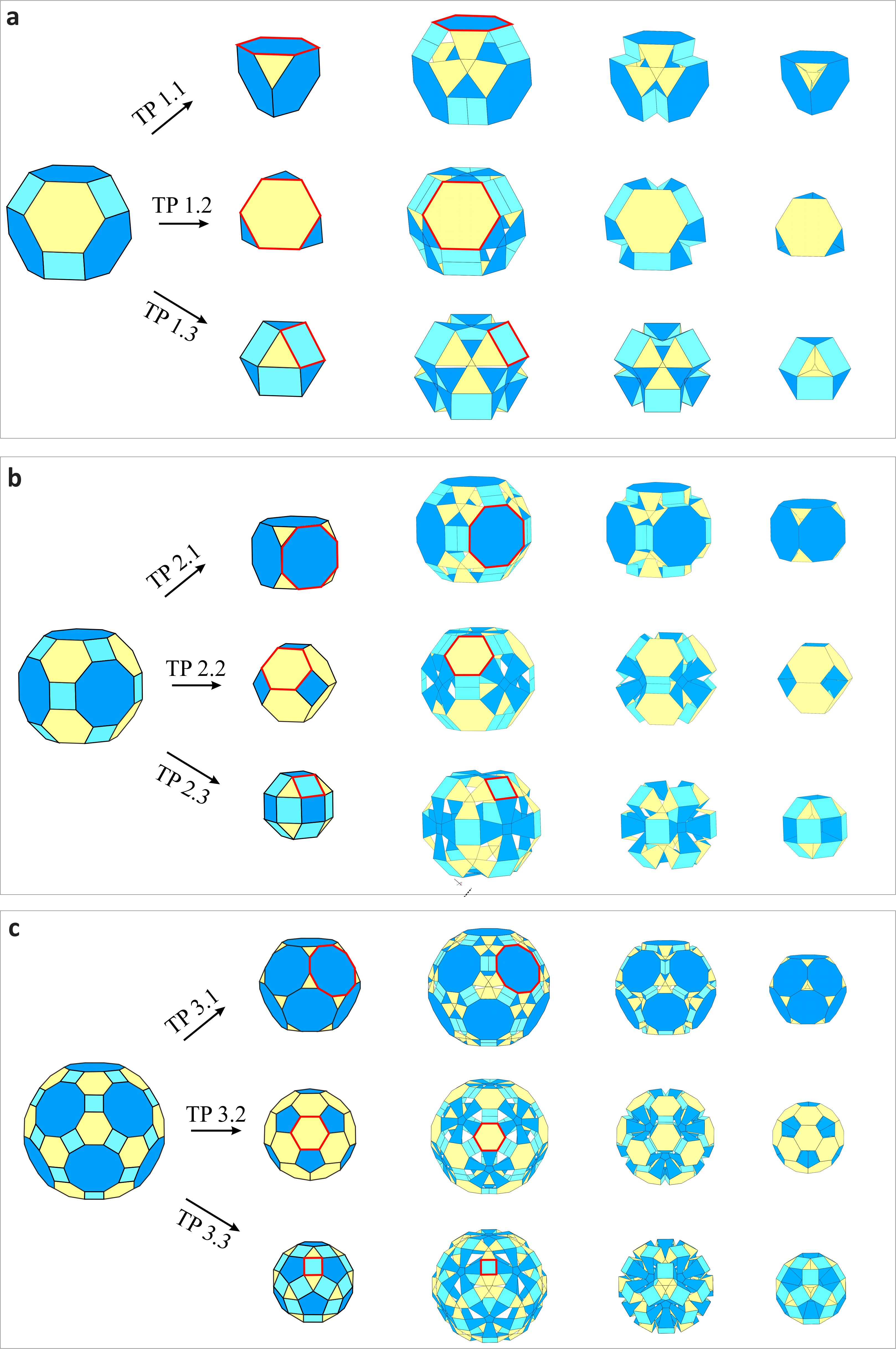
导读

        可变换多面体是一种特殊的折展多面体，可以实现两个规则多面体的空间构型切换，此类设计需要融合立体几何学和机构运动学的巧妙灵感，以及对于空间对称性的研究探索。然而，现有可变换多面体设计中的配对方案较为单一，如何利用机构运动学策略获得丰富的单自由度多面体变换方案仍具有挑战性。

        近日，天津大学机械工程学院陈焱教授团队联合英国索尔福德大学魏国武教授，基于阿基米德立体几何中可能的多面体变换配对方案，提出了一系列基于空间七杆机构的剪纸多面体，用机构学的策略实现了几何中的对称变换。该成果于2025年9月23日在线发表于《Small Structures》期刊，论文通讯作者为天津大学陈焱教授，第一作者为天津大学博士后顾元。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

研究内容

        研究人员在基于空间九杆机构的剪纸图案内部添加额外的面板和折痕，获得了一种单自由度三重对称的剪纸图案，其运动学模型可视为三重对称的空间七杆机构网格，同理亦可构建多重对称的空间七杆机构网格。由于空间七杆机构单元的平动特性，此类机构网格均具有单自由度同步运动。将多重对称的机构网格作为构建单元，按照相应的空间对称性依次嵌入至大斜方截半四面体、大斜方截半立方体、大斜方截半十二面体等阿基米德多面体表面，获得了一系列基于空间七杆机构网格的剪纸多面体机构 (图1)。

图1 基于空间七杆机构网格的剪纸多面体机构

        在此基础上，对于组成一个阿基米德多面体表面的三种多边形，通过依次选择保留一种多边形而折叠其余两种的方式，获得了更为丰富的单自由度多面体径向变换方案，并分别按照四面体对称性(Td)、立方体对称性(Oh)、十二面体对称性(Ih)的顺序在图2进行演示(视频1-3)。

图2 具有四面体对称性(Td)、立方体对称性(Oh)、十二面体对称性(Ih)的多面体变换方案

视频1

视频2

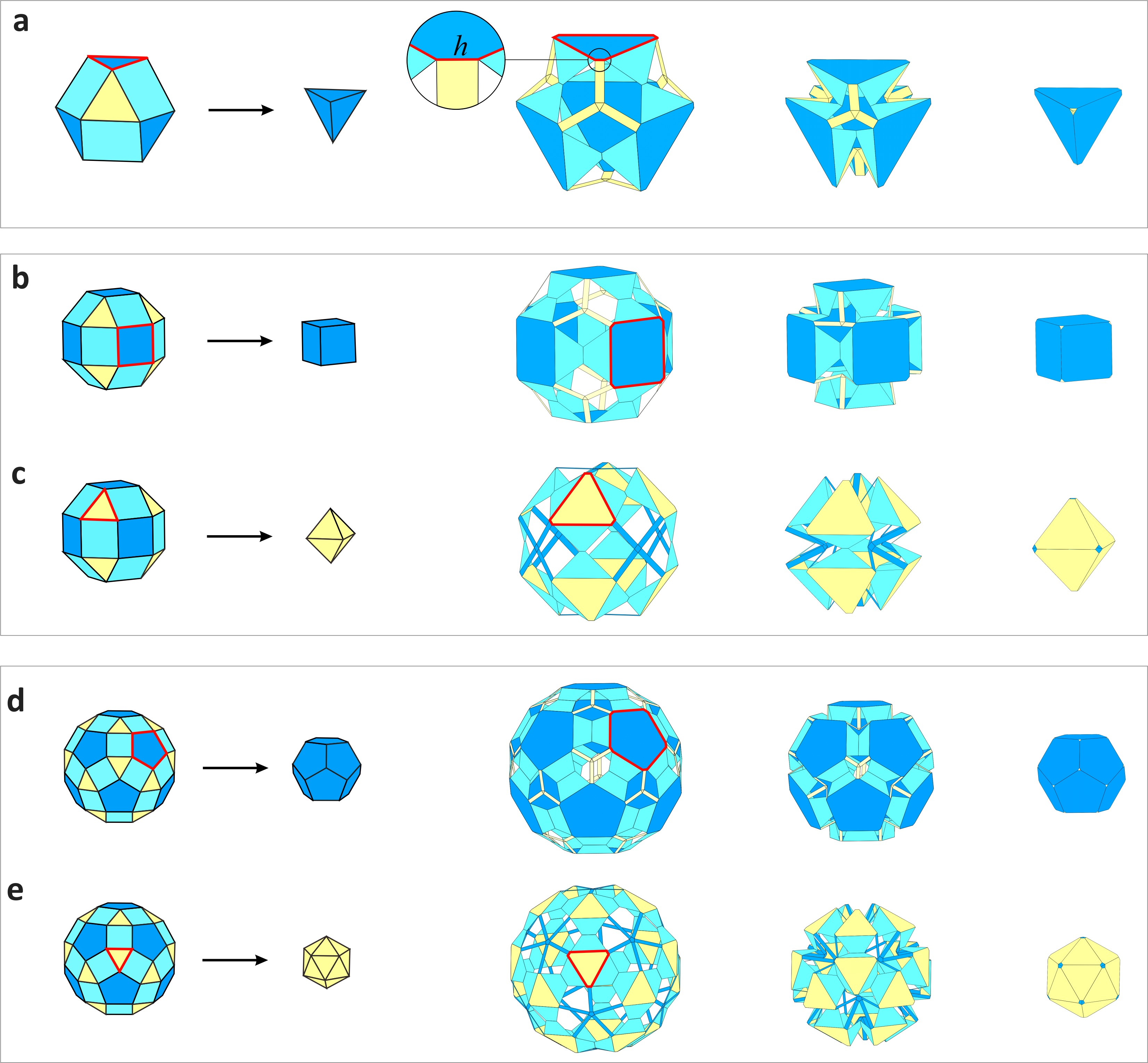
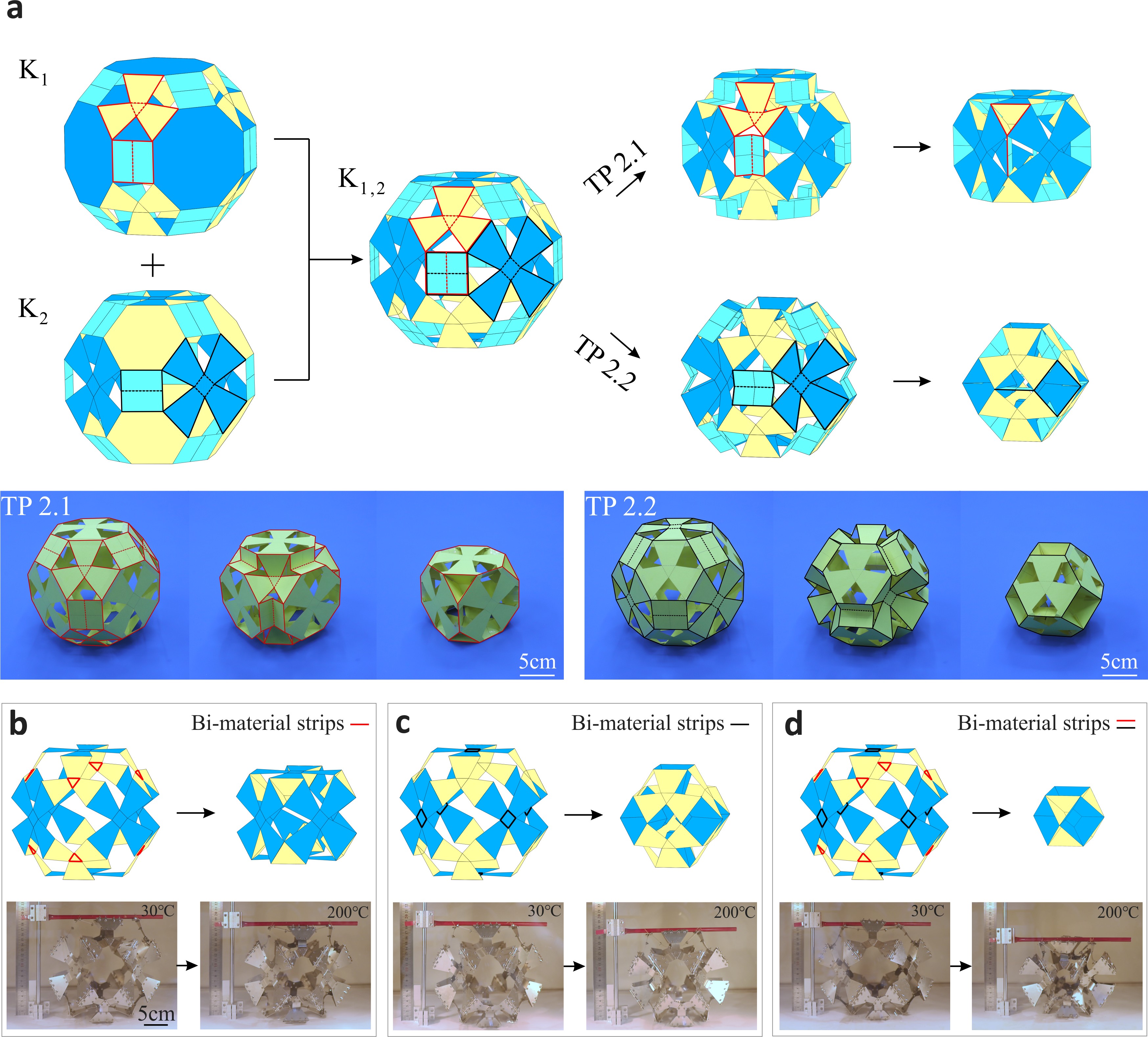
视频3

        进一步，基于所提出的剪纸多面体构建策略与径向对称变换原则，还可以通过调整面板与折痕的几何参数来探索从阿基米德多面体到柏拉图多面体的变换方案（图3），其机构拓扑仍为空间七杆机构网格。至此，此研究在11种阿基米德多面体和5种柏拉图多面体之间，利用多重对称的空间七杆机构网格共获得了5种四面体群变换方案、7种立方体群变换方案以及7种十二面体群变换方案。

图3 阿基米德多面体到柏拉图多面体的变换方案

        随后，以大斜方截半立方体为例，将两种已获得的折痕图案进行叠加，构建了具有两种不同折叠路径的可重构剪纸多面体，其中每一个折叠路径都保留了原始图案的单自由度径向运动特性（图4a）（视频4）。另一方面，通过去除上述可重构剪纸多面体中具有交叉折痕的方形面板，并引入双金属片作为驱动折痕，在图4b-d所示不同驱动布局下构建了三种负热膨胀多面体超材料胞元，都展现出正交各向同性的负热膨胀特性(视频5-7)。

图4 可重构多面体机构与负热膨胀多面体超材料

视频4

视频5

视频6

视频7

总结

        综上所述，此研究融合立体几何学和机构运动学理论，构建了一系列单自由度径向运动的剪纸阿基米德多面体，在阿基米德和柏拉图这两类典型多面体之间提出了丰富的变换方案，同时展示了此类剪纸多面体的可重构能力与热响应特性。该论文所提出的剪纸多面体机构及其变换方案为空间折展结构与多功能超材料的创新设计提供了新的灵感与思路。

Yuanqing Gu, Guowu Wei, Chuhan Xu, Yan Chen*. Kirigami Archimedean polyhedrons with one-degree of freedom radial transformation. Small Structures. 2025: e202500343.
(https://doi.org/10.1002/sstr.202500343)