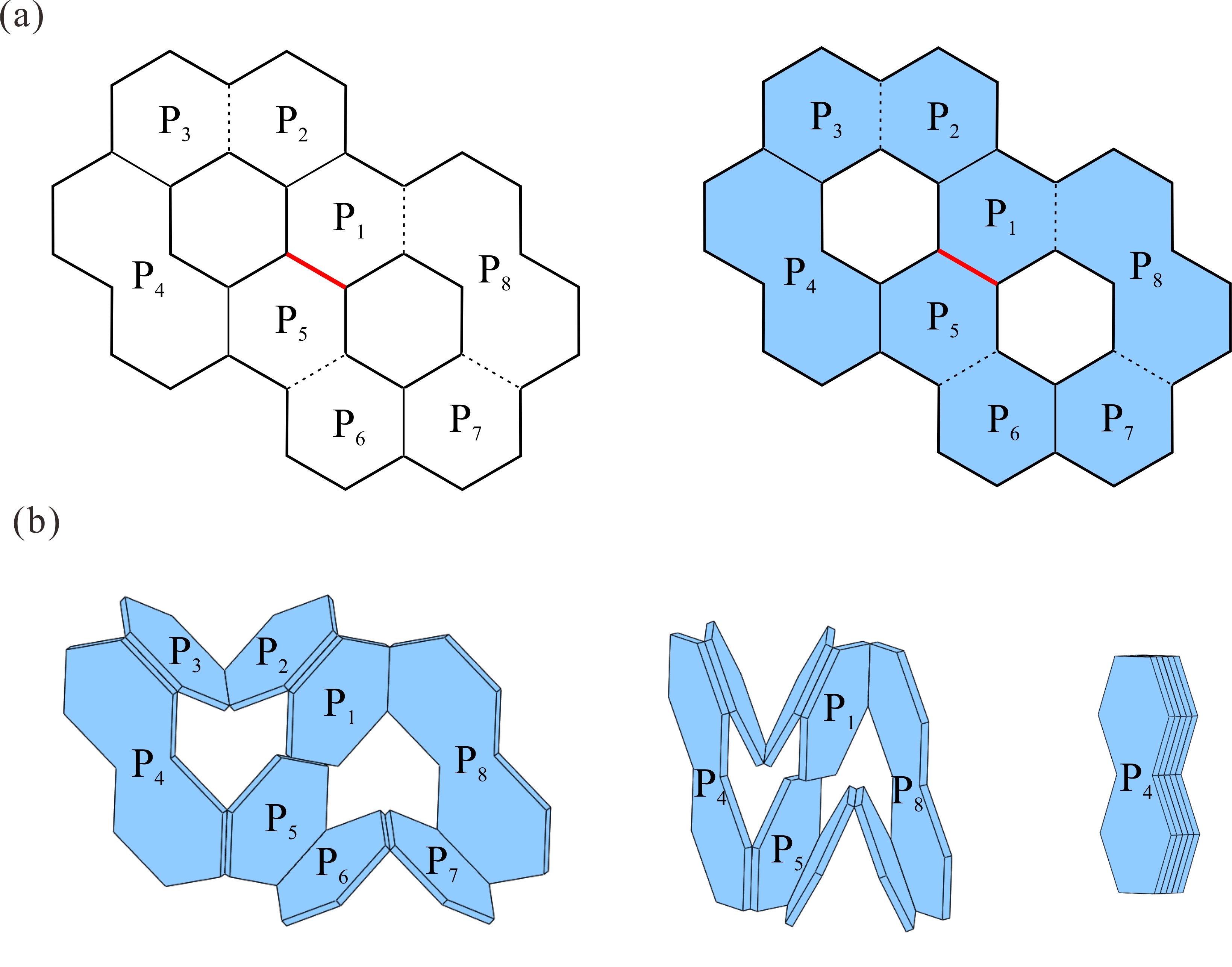
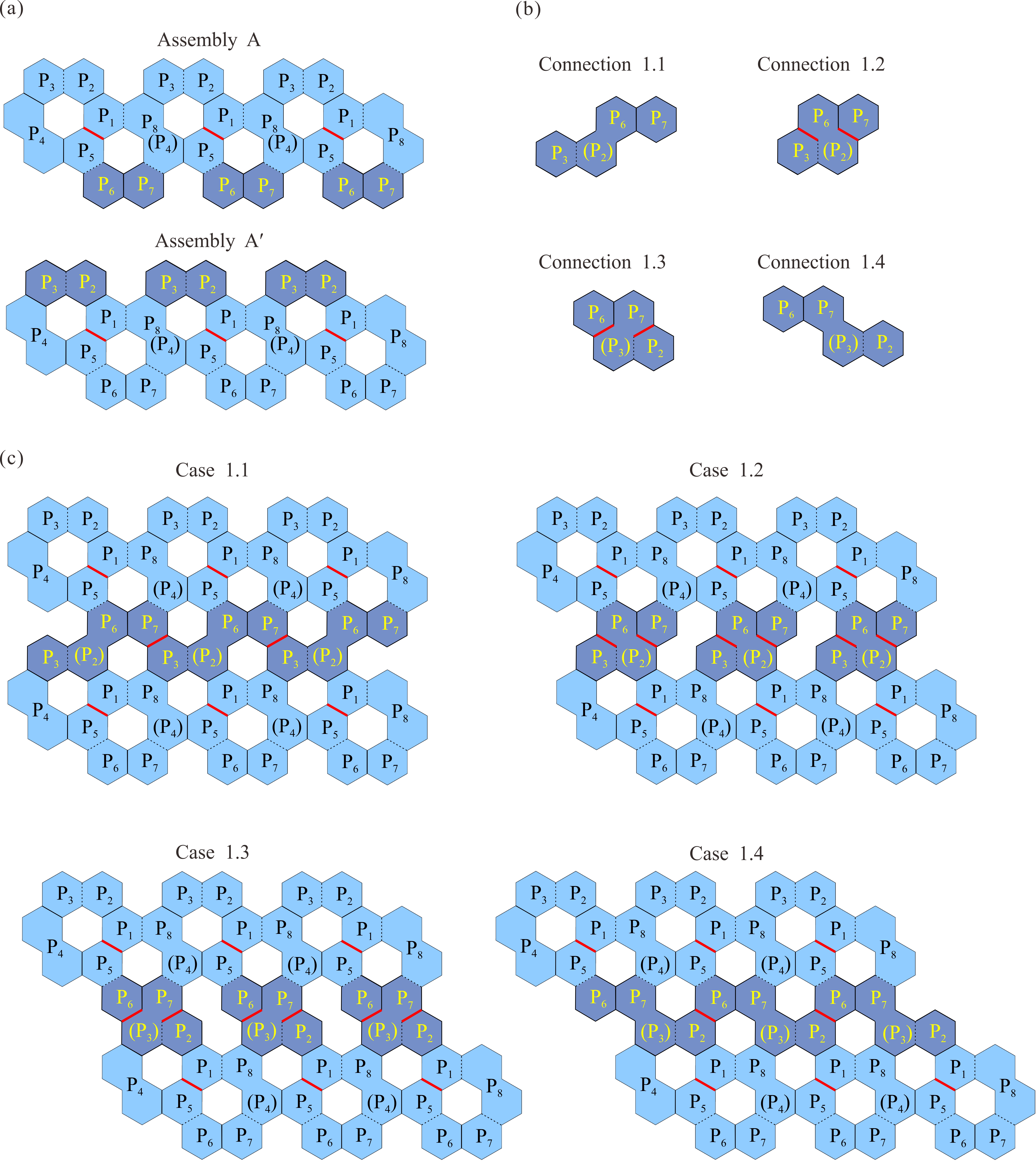
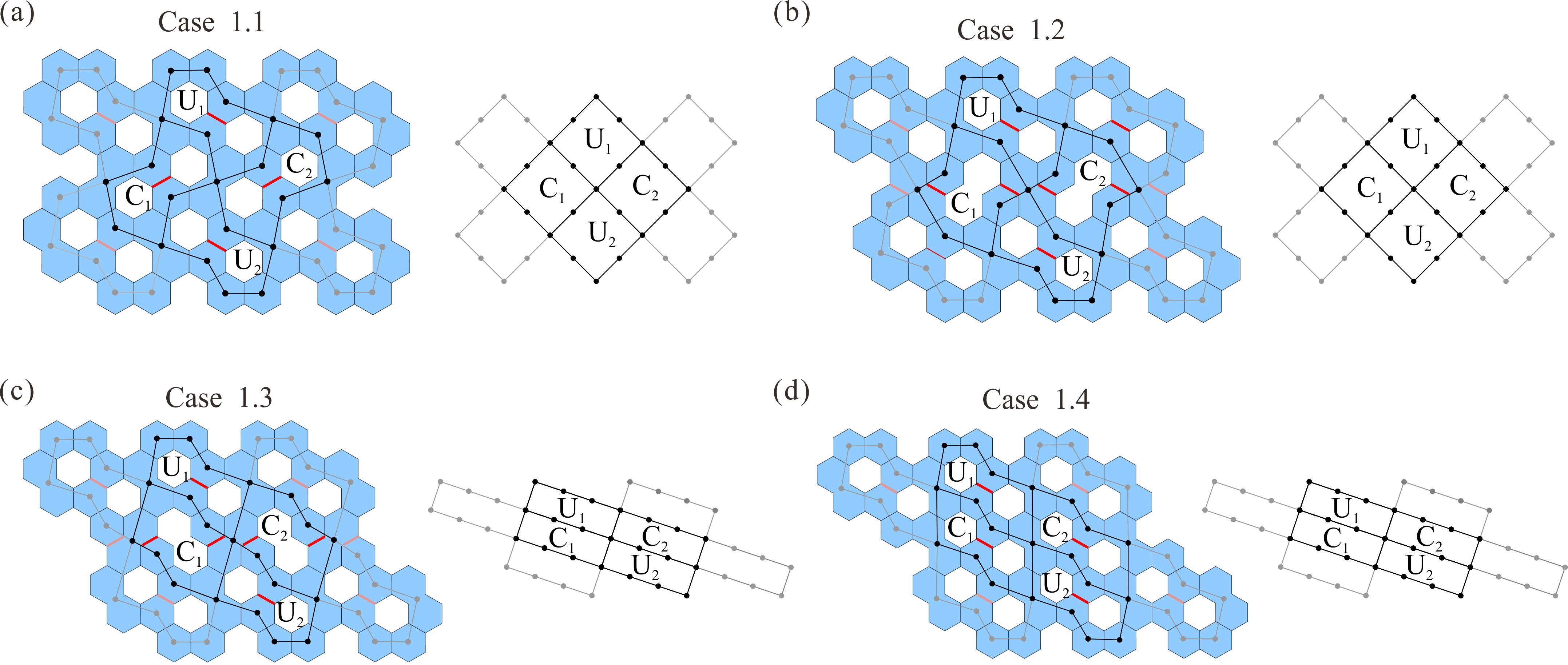
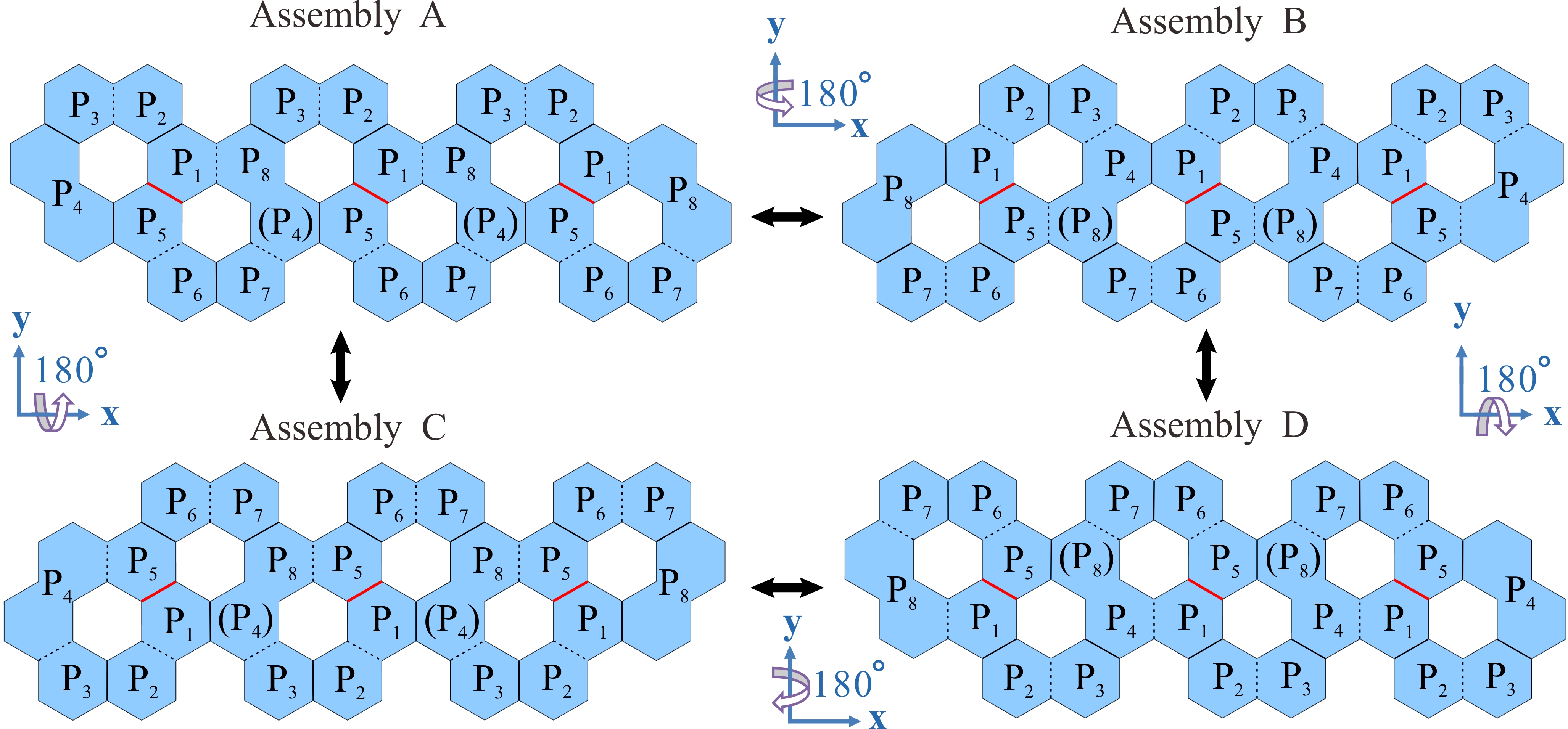
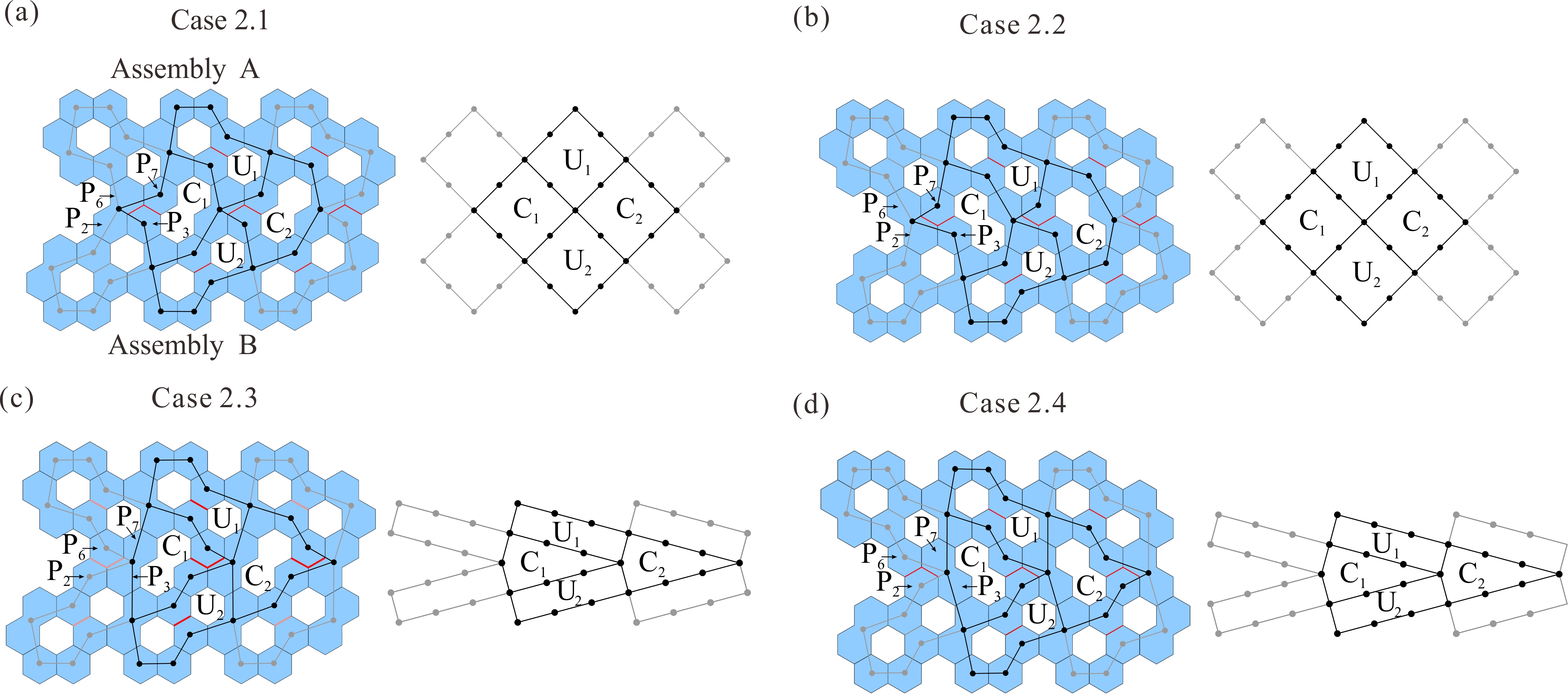
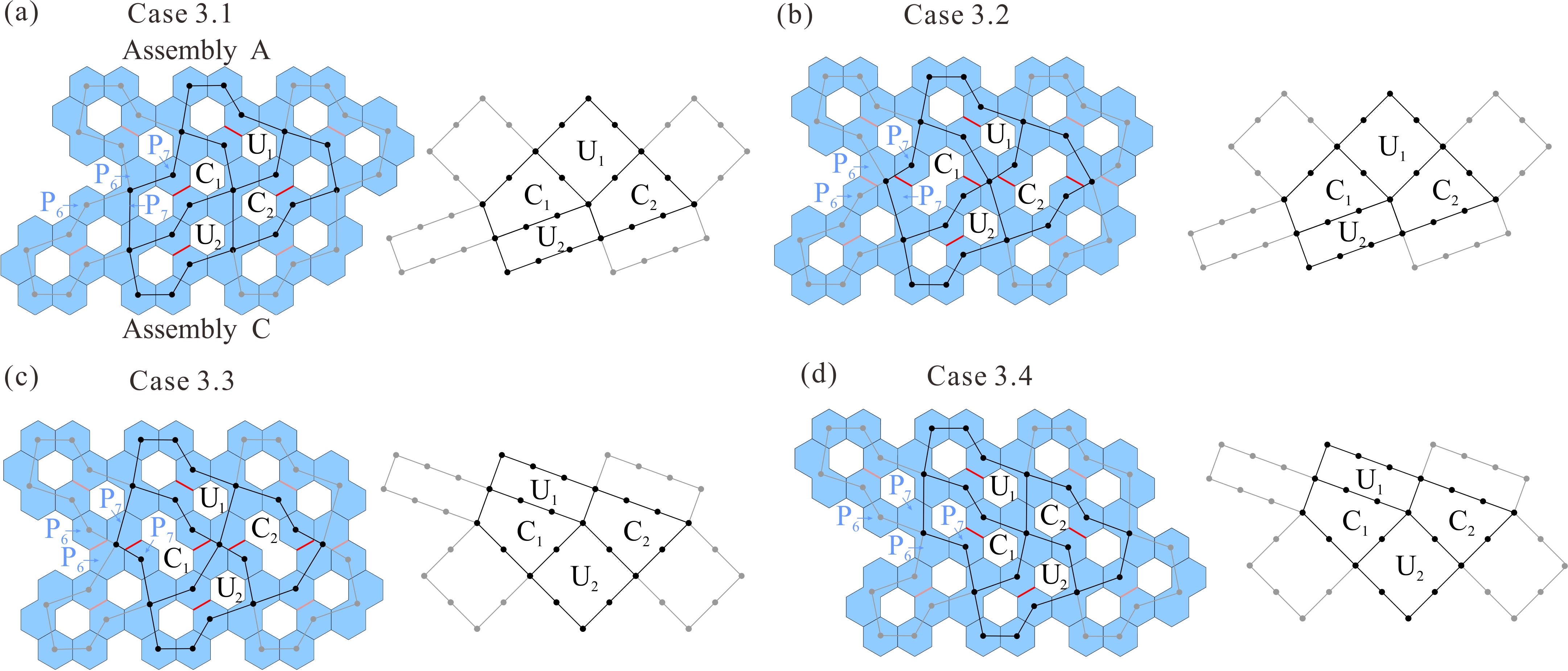
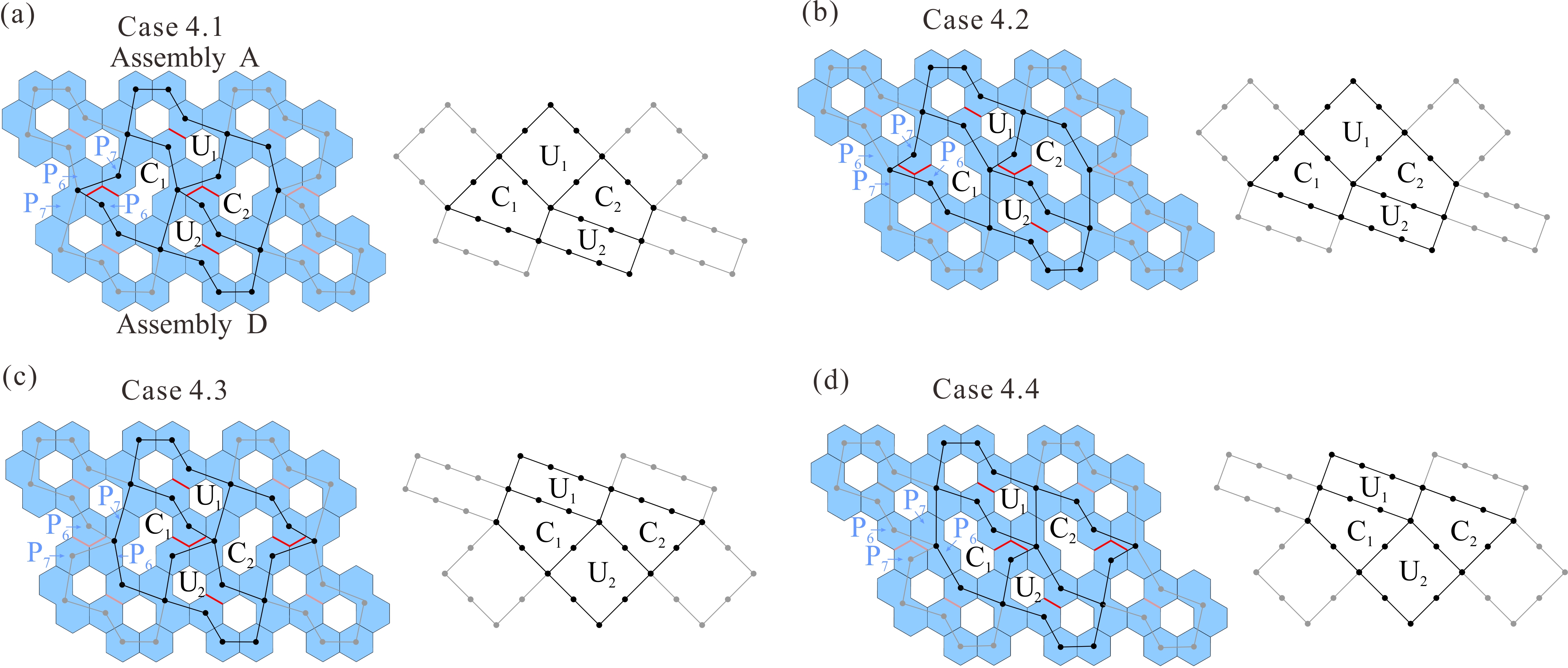
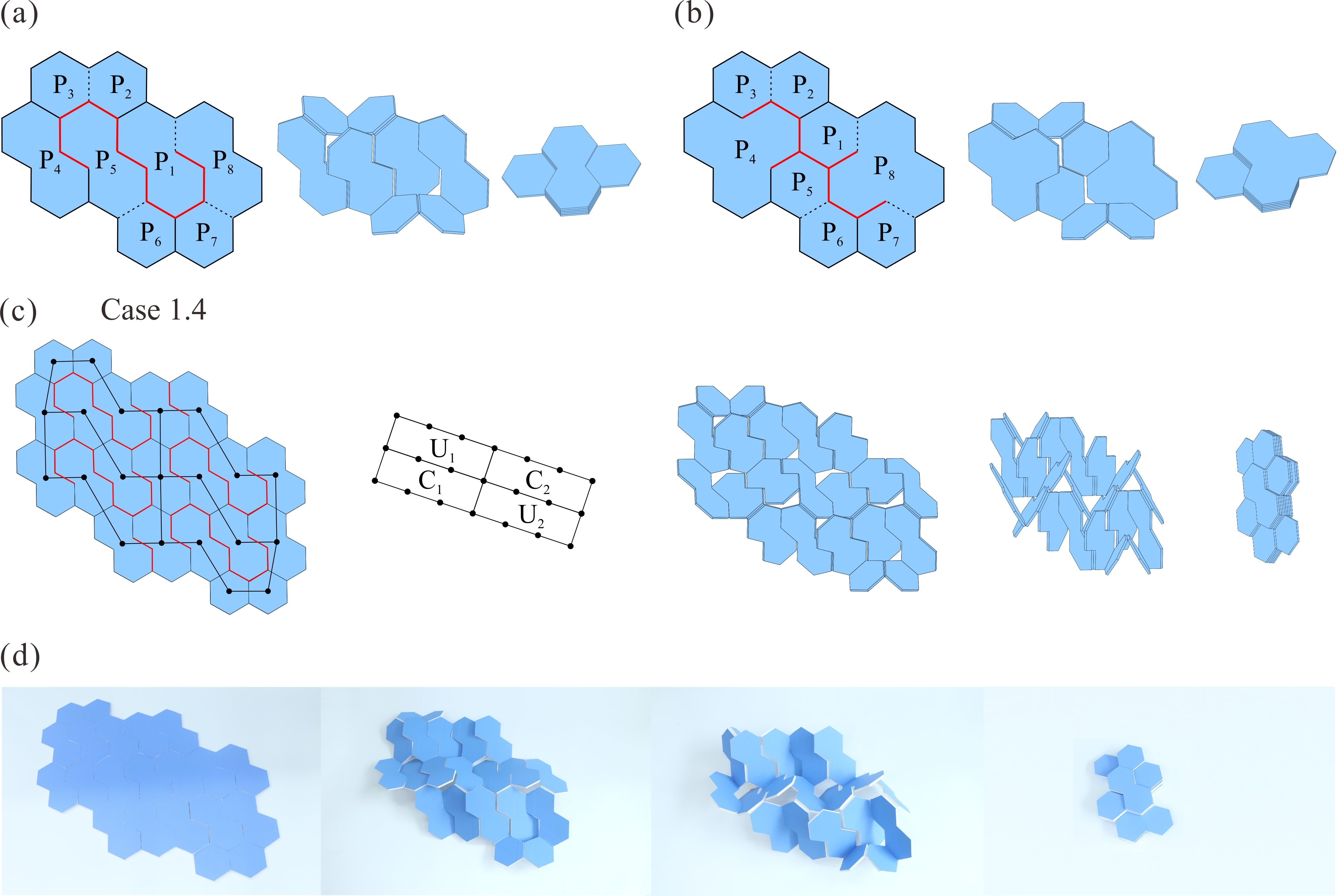
平面厚板折纸考虑了太阳能电池板和阵面天线等工程要求的面板厚度，在航空航天领域得到广泛应用。然而，如何利用形状规则的面板单元构建具有均匀厚度、平整展开表面、紧密折叠、单自由度特性的平面厚板折纸仍然是一大难题。

        近日，天津大学机械工程学院陈焱教授团队联合英国牛津大学由衷教授，以等厚度正六边形面板为基础，利用单自由度空间八杆机构网格构建了一系列具有等厚平整表面与紧密折叠特性的单自由度平面厚板折纸机构。该成果于2025年10月10日在线发表于Mechanism and Machine Theory期刊，论文通讯作者为天津大学陈焱教授，第一作者为天津大学博士后顾元庆。该研究由国家自然科学基金、腾讯基金（科学探索奖）资助完成。

        六边形作为蜂窝图案的基本几何元素，具有优异的镶嵌性能，因此本文采用等厚六边形面板作为平面厚板折纸的基本构件。如图1所示，P₁、P₂、P₃、P₅、P₆、P₇为正六边形面板，P₄、P₈分别为两个正六边形面板的组合，其中P₁和P₅面板之间设置了一条切线(红色所示)，此时上述首尾相连的八个面板组合可等效为空间八杆机构。如其运动序列所示，6个正六边形面板在P₄和P₈之间可完成有序的紧密折叠。

图1 以等厚度正六边形面板为基础的空间八杆机构单元

        在此基础上，探索上述空间八杆机构单元的镶嵌与连接形式，以构建大型平面阵列。首先，如图2(a)所示，将三个单元沿水平方向镶嵌，两个相邻单元共用一个面板(P₈/P₄)以构建出阵列A及其相同的阵列A'。随后，按照图2(b)所示的四种连接形式，将阵列A的面板P₆和P₇与阵列A'的面板P₂和P₃进行连接，最终获得图2(c)中的四种大型平面阵列构建方案。

图2 基于阵列A的大型平面阵列构建方案

        通过折叠角度与运动协调关系分析，验证了构建方案1.1至1.4均具有单一自由度。在图3所示的对应空间八杆机构网格拓扑中，由两个原始折叠单元 U₁和 U₂ 以及两个衍生的连接单元C₁和C₂组成的机构网格，可视为此类机构网格的最小单自由度拓扑单元，并具有平面无限拓展能力。

图3 构建方案1.1至1.4及其机构网格拓扑

         进一步，以阵列A为参考，在保持所有拓扑连接的情况下围绕x轴或y轴进行180度翻转，可生成图4所示的阵列B、C和D。参照图2中阵列A与A'的四种连接形式，阵列A 与阵列B、C 和 D可分别按照四种形式进行连接以构建大型平面阵列，具体构建方案及其单自由度空间八杆机构拓扑分别如图5-7所示。至此，本文共获得16种以等厚度正六边形面板为基础的平面厚板折纸构建方案，及其8 种单自由度机构拓扑。

图4 围绕x轴与y轴旋转变换的阵列A至D

图5 构建方案2.1至2.4及其机构网格拓扑

图6 构建方案3.1至3.4及其机构网格拓扑

图7 构建方案4.1至4.4及其机构网格拓扑

        最后，基于所获得的单自由度机构拓扑进一步研究上述平面厚板折纸机构的表面完整性。如图8(a-b)所示，通过引入额外六边形厚板以补充面板间的空隙，在厚板结构运动过程中不发生物理干涉的条件下，获得两种具有平整展开表面的空间八杆机构折叠单元。以构建方案1.4为例，图8(c)展示了具有完整且平整展开表面的平面厚板折纸设计方法，其实物模型折叠序列如图8(d)所示（视频1）。

图8 六边形平面厚板折纸的表面完整性设计

视频1

        综上所述，此工作深入探索了空间八杆机构的单自由度拓扑组合，以等厚度正六边形面板为基础，提出了一系列具有均匀厚度、平整展开表面、紧密折叠、单自由度特性的平面厚板折纸构建方案。本文研究了基于不同面板连接形式的多种厚板折叠方案及其机构拓扑，未来的研究可扩展至其他多边形面板的折叠阵列，从而进一步增强平面厚板折纸机构的通用性与适用性。

Yuanqing Gu, Li Wen, Jiayao Ma, Xiao Zhang, Zhong You, Yan Chen*. One-DOF hexagonal thick-panel origami with uniform thickness, flat deployable surface and compact folding. Mechanism and Machine Theory. 2025, 217, 106252.
(https://doi.org/10.1016/j.mechmachtheory.2025.106252)