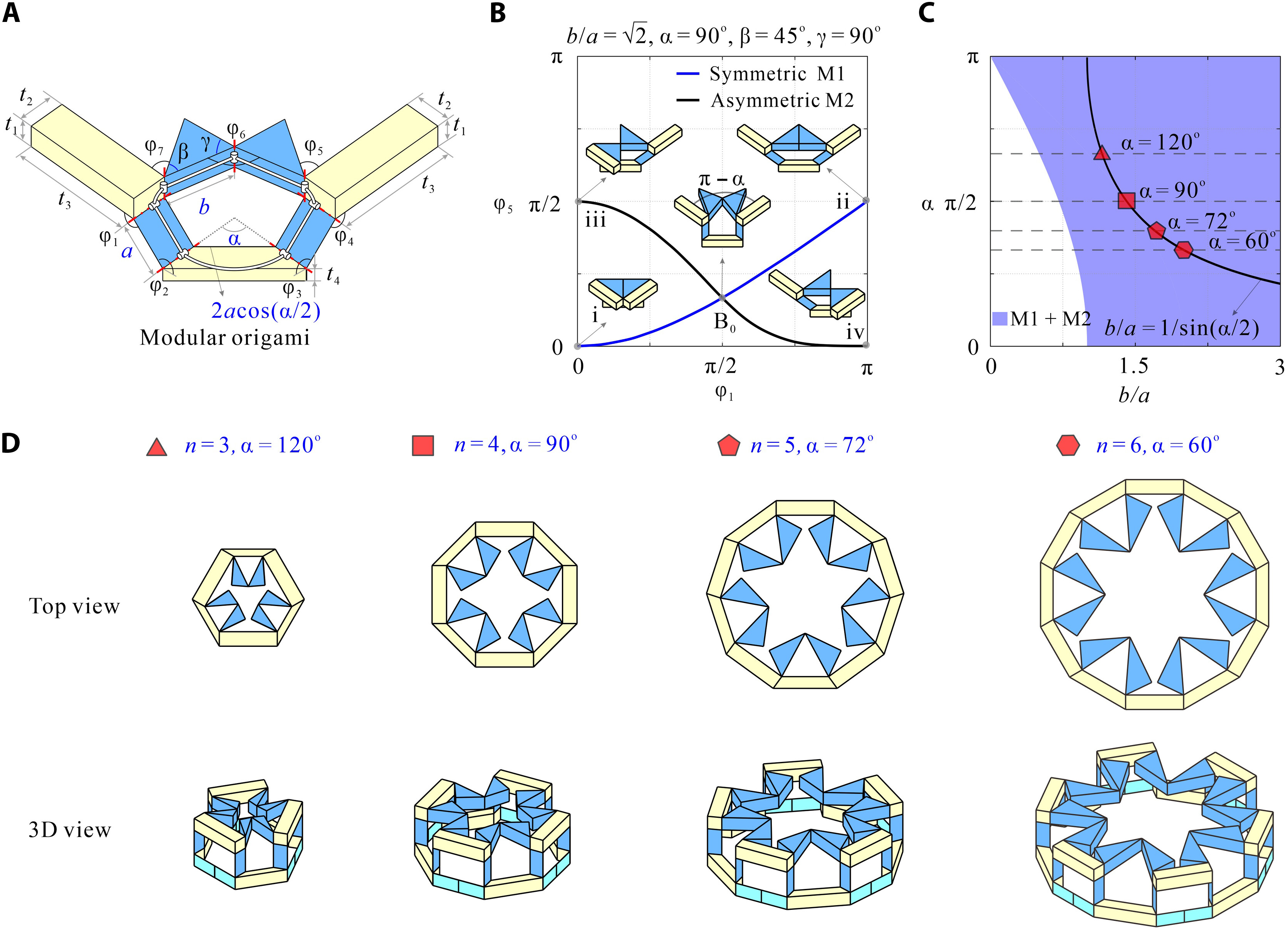
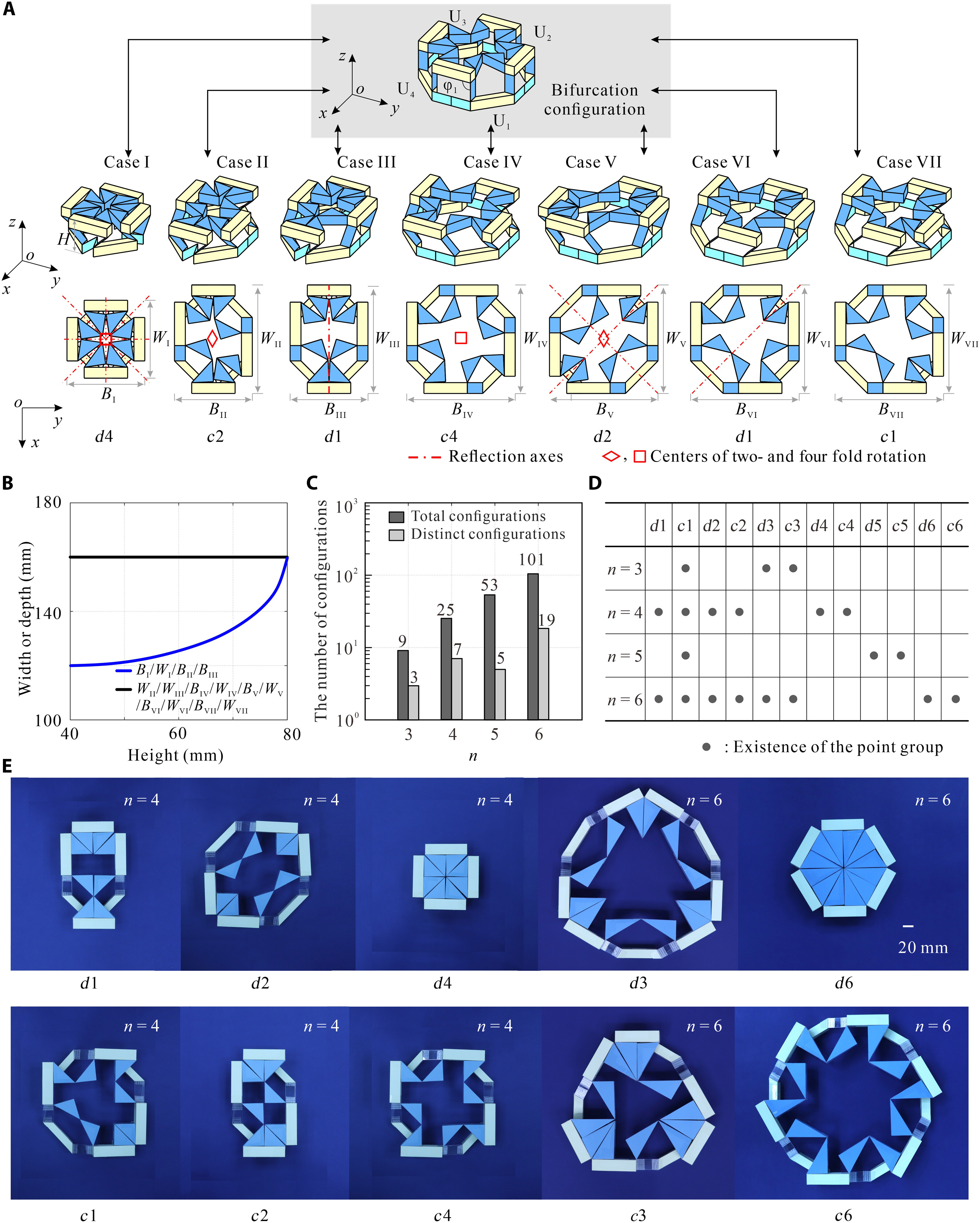
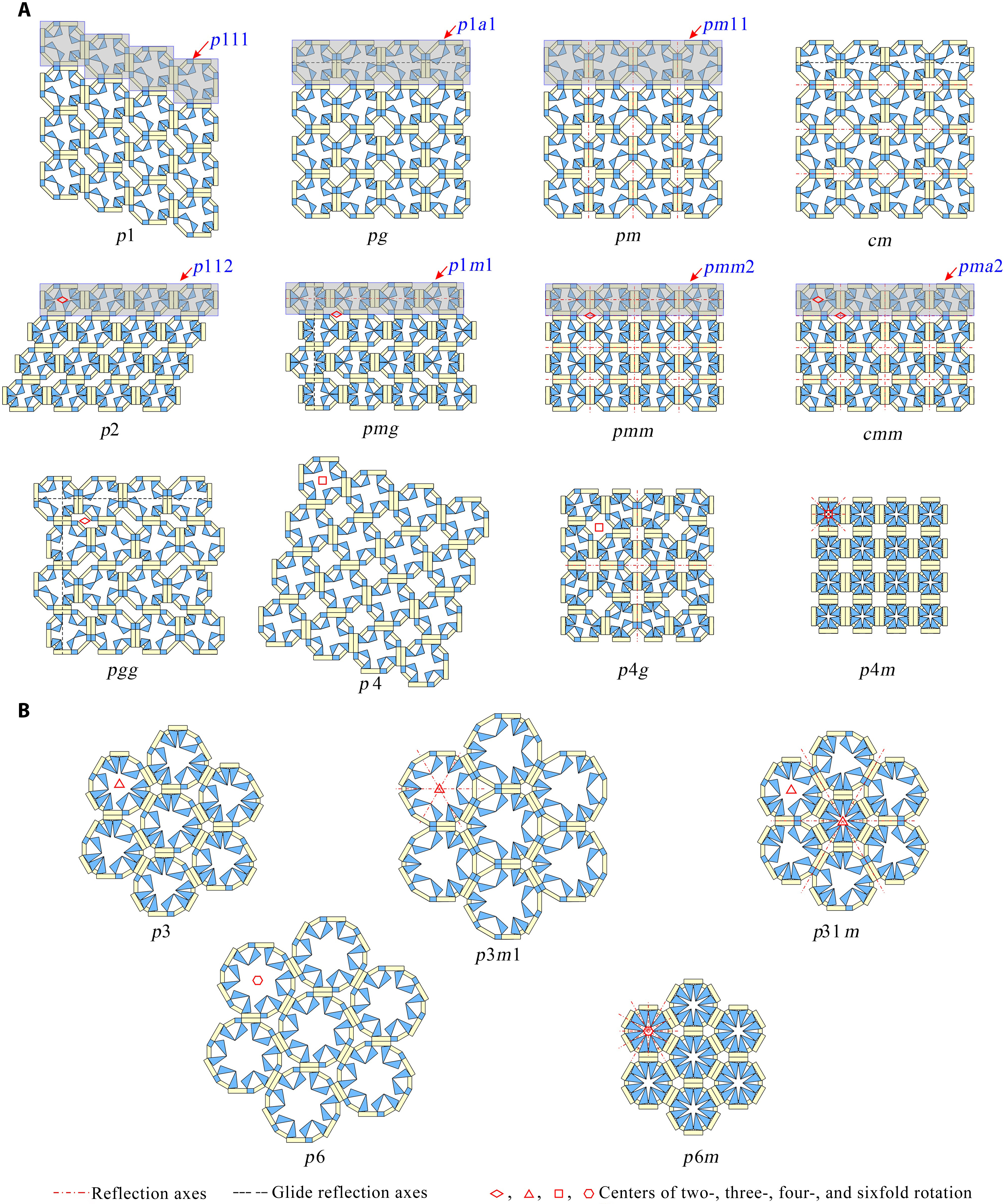
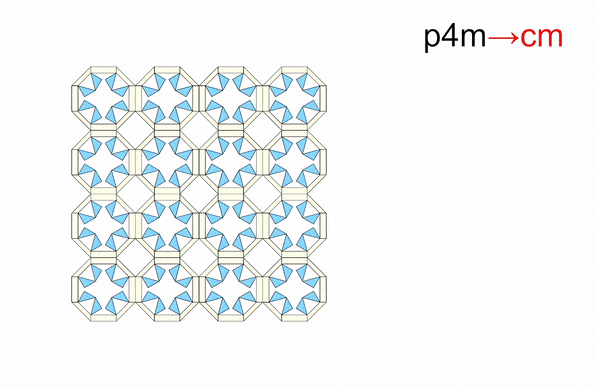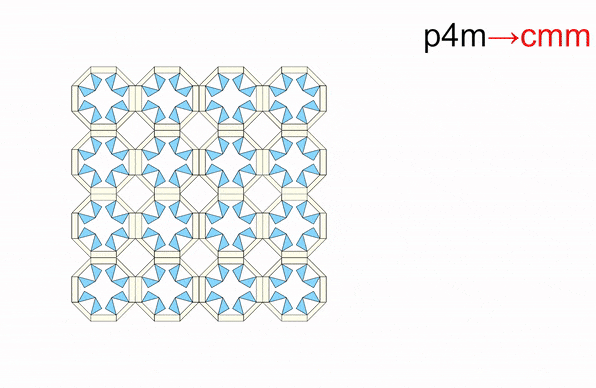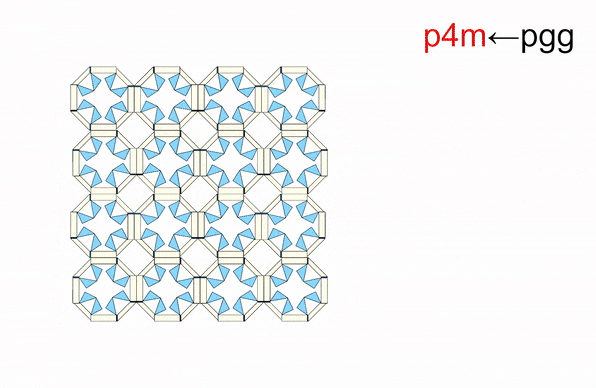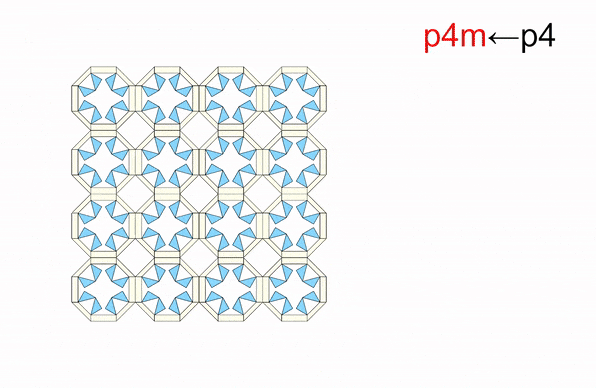
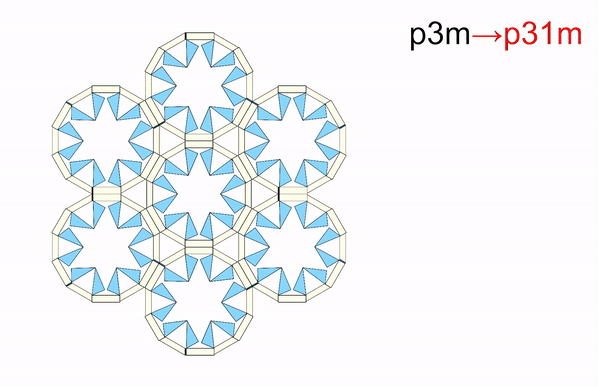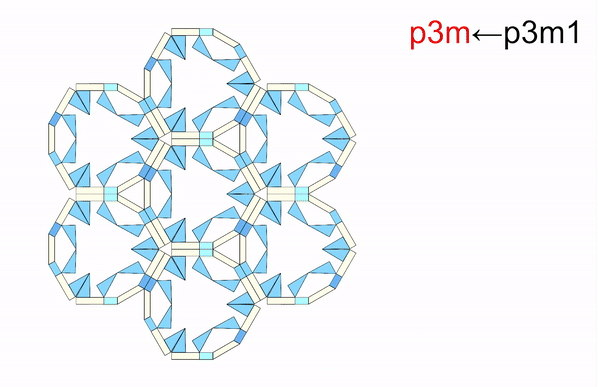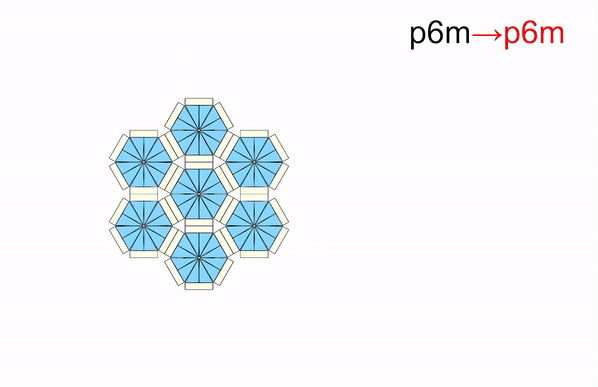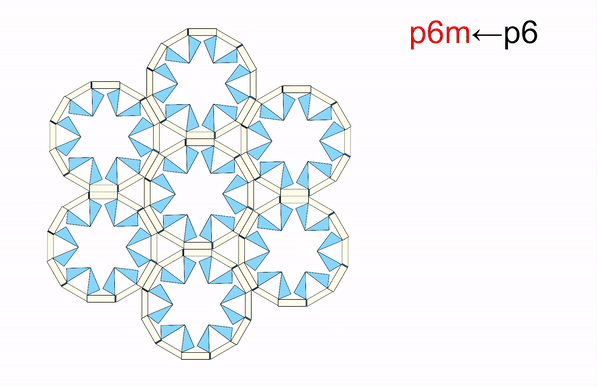
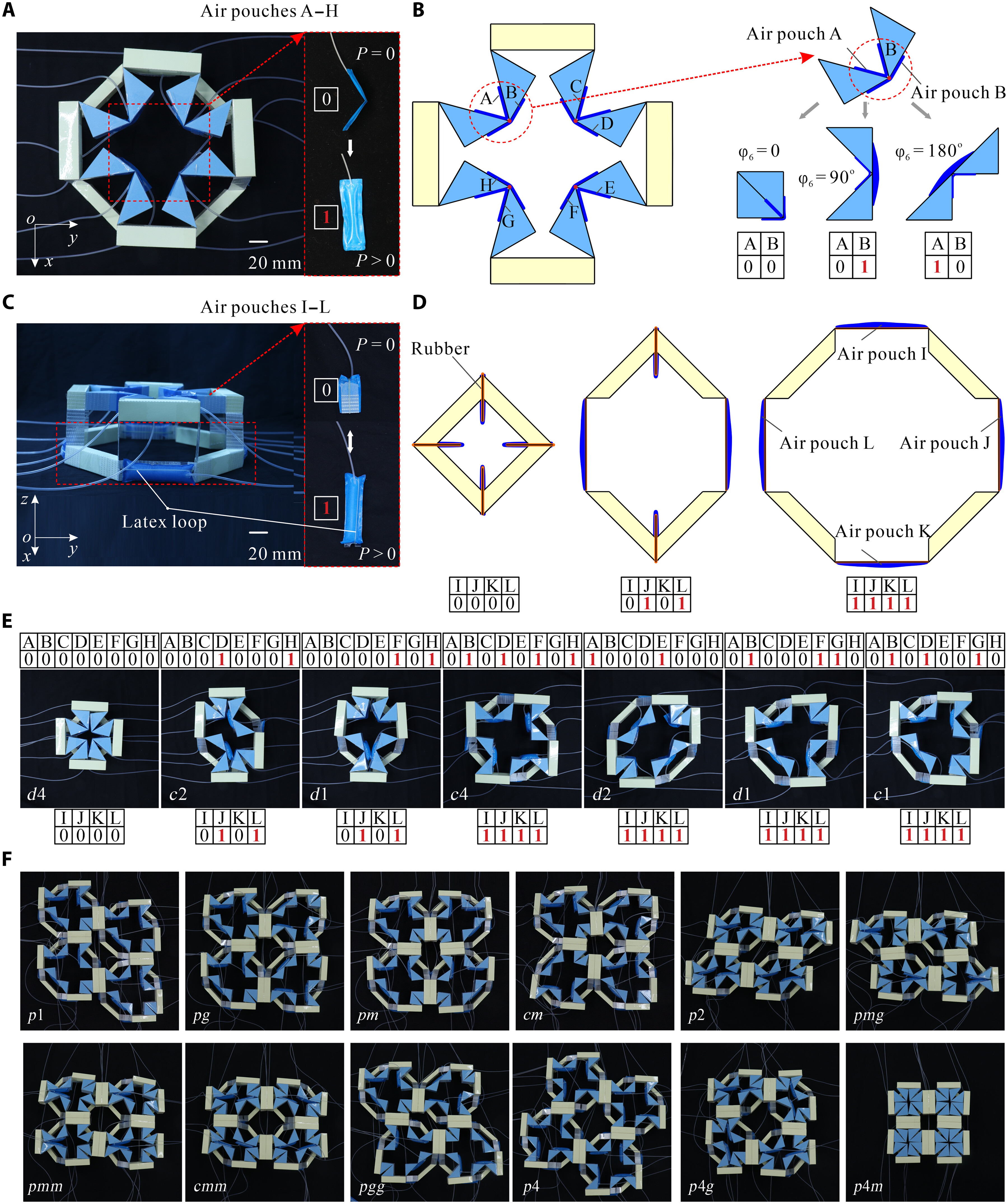
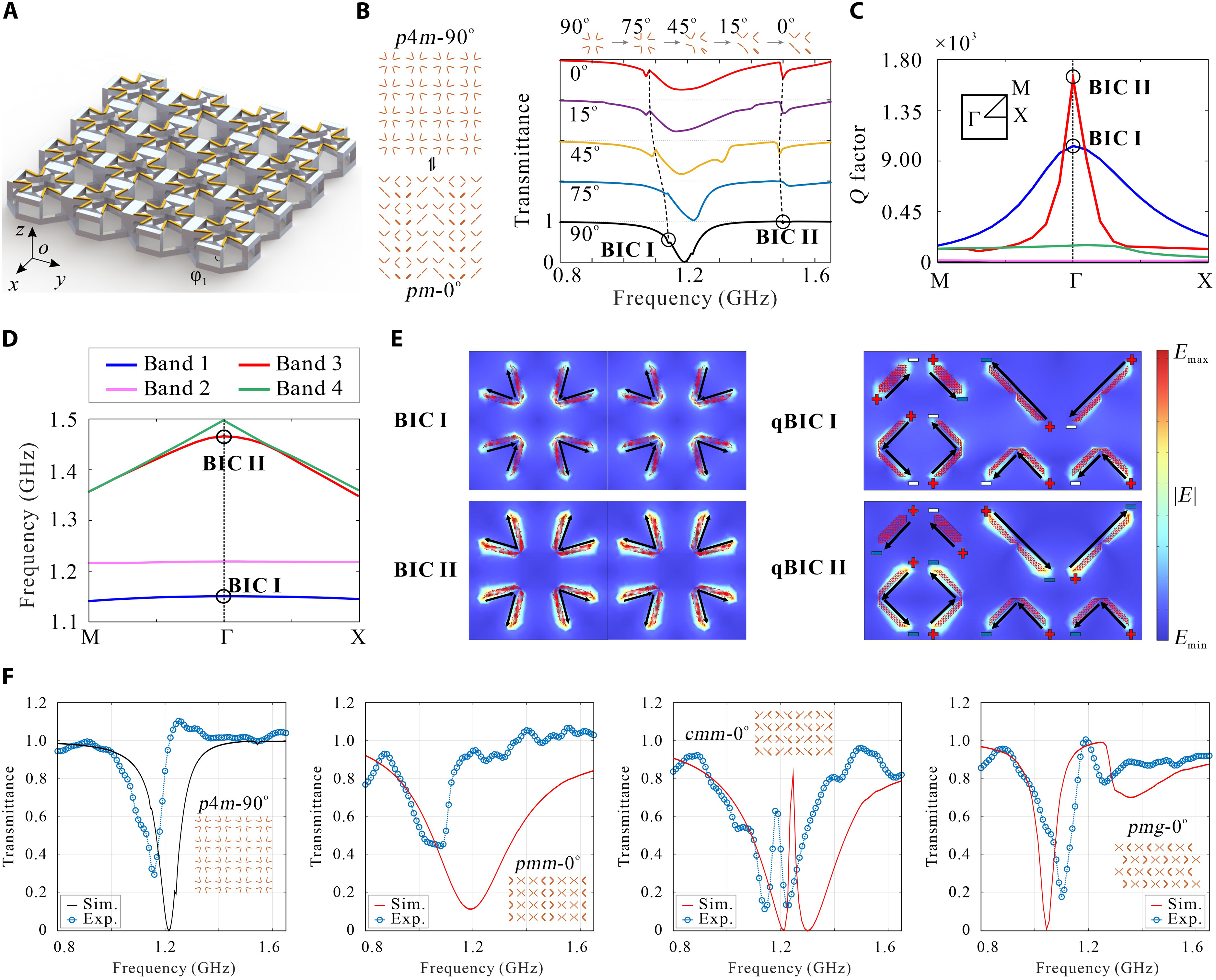
导读

        从雪花的六角晶瓣，到蝴蝶的斑斓翅膀，从古希腊的神庙石柱，到伊斯兰的繁复花纹，对称结构始终展现出一种和谐与平衡之美。然而在科学家眼中，对称性远不止于视觉美学，更是决定材料物理性能的隐藏法则，深刻影响着光、电、声与物质的相互作用。传统材料和结构一旦制造完成，对称性便固定不变。如何让结构“活”起来，在不同对称形态间自由切换，从而赋予其前所未有的多功能特性，一直是该领域的核心挑战。

        近日，天津大学陈焱教授团队与西湖大学姜汉卿教授团队合作，在《Science Advances》上发表题为“Reconfigurable modular origami for tunable 2D symmetry groups”的研究论文。该研究受模块化折纸启发，设计了一种基于运动学分岔的单自由度可重构模块，仅用两套模块化镶嵌，即可在气动驱动下动态、可逆地实现全部17种二维空间群（又称“壁纸群”）间的变换，并成功演示了利用对称性调控电磁连续域束缚态的潜力。该成果首次实现了二维对称群的全覆盖调控，为可编程机电耦合电磁超表面的发展开辟了新途径。论文通讯作者为西湖大学姜汉卿教授与天津大学陈焱教授，第一作者为天津大学机械工程学院刘伟奇助理研究员和电气自动化与信息工程学院任群副研究员。天津大学马家耀教授、西湖大学博士后张壮也为本研究作出了重要贡献。该研究由国家自然科学基金、腾讯基金（科学探索奖）、国家重点研发计划“智能机器人”重点专项资助完成。该论文还被选为本期精选图片。

        研究团队从模块化折纸中找到了对称性调控难题的破解之道。他们先设计了一种单自由度模块折纸单元，其运动学上等效于空间七杆机构（图1）。该单元具有一个关键特性：运动学分岔。当折纸单元运动到一个特定状态（分岔点，φ₁=π/2）时，选择路径M1：模块的两个矩形面板反向摆动，模块保持平面对称。选择路径M2：两个矩形面板同向摆动，模块的对称性被打破。正是这个简单的“二选一”机制，为后续千变万化的对称模式埋下了伏笔。接着，研究团队像玩高级乐高一样，将多个单元（如3、4、5、6个）环形排列，组装成“n单元对称模块”。

图1 n单元对称模块的构造

        由于n个单元构成的模块具有n重对称性，其单自由度特性和运动分岔得以保留。以四单元模块为例，在分岔点时，4个单元各自有2种路径选择，组合起来就像一个4位二进制密码，从而产生16种可能的运动模式。经过运动学筛选，最终获得了7种截然不同的对称构型，分别对应d4, c4, d2, c2, d1,和c1等点群（图2）。研究团队还分析了 3、5 和 6 单元对称模块的运动分岔和对称性变化：3 单元模块覆盖d3、c3、c1 点群；5 单元模块覆盖d5、c5、c1 点群；6 单元模块覆盖d6、c6、d3、c3、d2、c2、d1、c1 点群。由此可见通过将n个单元沿 z 轴圆周排列，可得到任意 dn 或 cn 点群的n单元对称模块。其中，四单元模块擅长生成与2重、4重相关的对称，而六单元模块则能产生3重和6重相关的对称。两者结合，便完整覆盖了全部10种晶体学点群：d1、d2、d3、d4、d6、c1、c2、c3、c4、c6。

图2 n单元对称模块的分岔重构与2D点群调控

        随后，研究团队开始用四单元模块按照统一的连接规则进行线性拼接生成条纹图案（图3）。例如，对 c1, c2 或 d1 点群模块施加平移操作，即可生成具有 p111，p112或 p1m1线群的条纹图。研究发现，通过重构每个模块的对称构型，单个条纹图案的整体对称模式就能呈现出全部7种线群（p111、p1a1、pm11、p1m1、p112、pma2 和 pmm2）。将这7种条纹图案在2D平面内平铺，就可以直接得到1重和2重旋转对称性相关的壁纸组。例如：将 p111、p112条纹图案直接堆叠，分别得到 p1、p2壁纸群；通过对 p1m1条纹图案进行滑移反射操作，即可得到 pmg壁纸群。4 重旋转对称性相关的壁纸组可通过对低对称性模块进行复合对称操作或直接使用高对称性模块平铺实现。例如，将 c2 点群的 4 单元模块进行四次旋转后双向平移，可生成 p4g 壁纸组；直接平铺d4点群的4 单元模块，即可得到p4m 壁纸组群。因此，只需要 4 单元模块的面内平铺就可以获得与1、2、4 重旋转对称相关的12 种壁纸组群（动图1）。而3 或 6 重旋转对称相关的壁纸组群（p3、p3m1、p31m、p6、p6m）则需要引入3 单元或 6 单元对称模块。例如，6 单元模块围绕中心模块形成蜂巢状结构，通过中心模块重构选择c3、d3、c6 或 d6点群，可实现 p3、p3m1、p6 或 p6m 壁纸组（动图2）。得益于模块的强大分岔重构能力，仅凭四单元和六单元模块这两套“基础乐高”，研究团队就从最基础的“零件”（10种晶体学点群），到中间的“条纹”（7种线群），再到壁纸组（17种空间群），最终构筑了整个二维对称宇宙的完整大厦。

图3 四单元和六单元模块构造的2D线群和空间群

动图1 由4单元模块构造的12种壁纸组

动图2 由6单元模块构造的5种壁纸组

         如此复杂的对称变化，控制起来会不会非常困难？答案出乎意料的简单。研究团队开发了一套双层气动控制系统（图4），通过向嵌入的气袋进行“二进制”充气（充气/不充气），即可精准控制模块的变形。上层“对称选择器”：由8个气袋组成，负责在分岔点“指挥”每个单元选择M1或M2路径，从而决定整体的对称类型。下层“展开驱动器”：由4个气袋与预拉伸乳胶圈构成的气腱耦合系统组成，负责控制整个模块的展开与收缩，改变其整体尺寸。通过给不同的气袋组合“发令”（如“00010001, 0101”），模块就能在几秒内从一种对称形态变换到另一种对称形态（动图3）。这种方法简单、可靠，且具有很强的容错性。更重要的是，这种基于二进制指令的分布式控制策略具有极佳的可扩展性。通过统一协调各模块的气动信号，该方案可直接推广至大尺度的镶嵌结构（动图4）。

图4 对称模块及其镶嵌的二进制气驱策略

动图3 单个4单元模块对称性调控实验演示

动图4 4单元模块构造的2x2镶嵌的对称性调控实验演示

        为了展示这种可调对称性结构的应用潜力，团队将金属天线阵列集成在可重构折纸基底上，制成智能“电磁超表面”，并在0.8–1.6 GHz 范围内进行了电磁仿真，从而揭示了对称保护的连续域束缚态向准束缚态的演化机制(图5)。研究发现，在高对称态 p4m-90° 构型下，共振模态的对称性与自由空间辐射通道不匹配，辐射被完全抑制，能量严格束缚于结构内部，形成对称保护型连续域束缚态(BIC)，表现出理论上无限大的品质因子 Q。当逐步调节折纸单元的二面角 φ₁（从 90° 下降至 0°）时，对称性依次降低为 pm-75°、45°、15°、0° 等状态。在此过程中旋转对称性被打破，仅保留镜面反射。这种保护性选择规则被解除，原本被禁锢的模式开始弱耦合至辐射场，演化为准束缚态(qBIC)。仿真结果表明，原先位于约 1.15 GHz 与 1.50 GHz 的两组 BIC 模式（Q 因子分别为 1628 与 1032）转化为可辐射的 qBIC I 与 qBIC II，对应透射谱中典型的非对称共振谷。电场分布分析进一步揭示了这种转变的内在机制，在 p4m-90° 状态下，电场矢量在相邻单元间呈等幅反向分布，导致远场辐射相互抵消；而当结构对称性降至 pm-0° 时，干涉抵消条件被破坏，能量泄露至外场。研究还将分析拓展至 12 种不同对称群构型，结果表明：高对称结构（如 p4m、pmm）对应完全束缚的 BIC，仅在谱中出现单一、窄带共振峰；具有全局手性或局部镜面对称（如 p1、p2、p4、cm、cmm、p4g）的体系，可激发多频点窄带共振，显著增强场能局域化；引入滑移反射（如 pg、pmg、pgg、p4g）后，对称性进一步削弱，仅能形成部分束缚态，表现为宽而浅的共振谷。为验证理论预测，研究团队制备并表征了多种典型超表面样品。实验测得的透射谱与仿真结果在共振位置和趋势上高度一致，证明了qBIC 的对称性选择规律。

图5 对称性可调控的电磁超表面

        综上所述，该研究将深奥的机构分岔理论、奇妙的折纸工程学与前沿的电磁调控融为一体，实现了从被动选择对称性到主动调控对称性的飞跃，为研究可编程超材料及新型光电器件提供了新思路。

Weiqi Liu#, Qun Ren#, Yunjie Wang, Zhuang Zhang, Xiuyu Wang, Yongshan Liang, Hao Huang, Jiayao Ma, Hanqing Jiang*, Yan Chen*. Reconfigurable modular origami for tunable 2D symmetry groups, Science Advances, 2025, 11, eady3812.
(https://www.science.org/doi/10.1126/sciadv.ady3812)