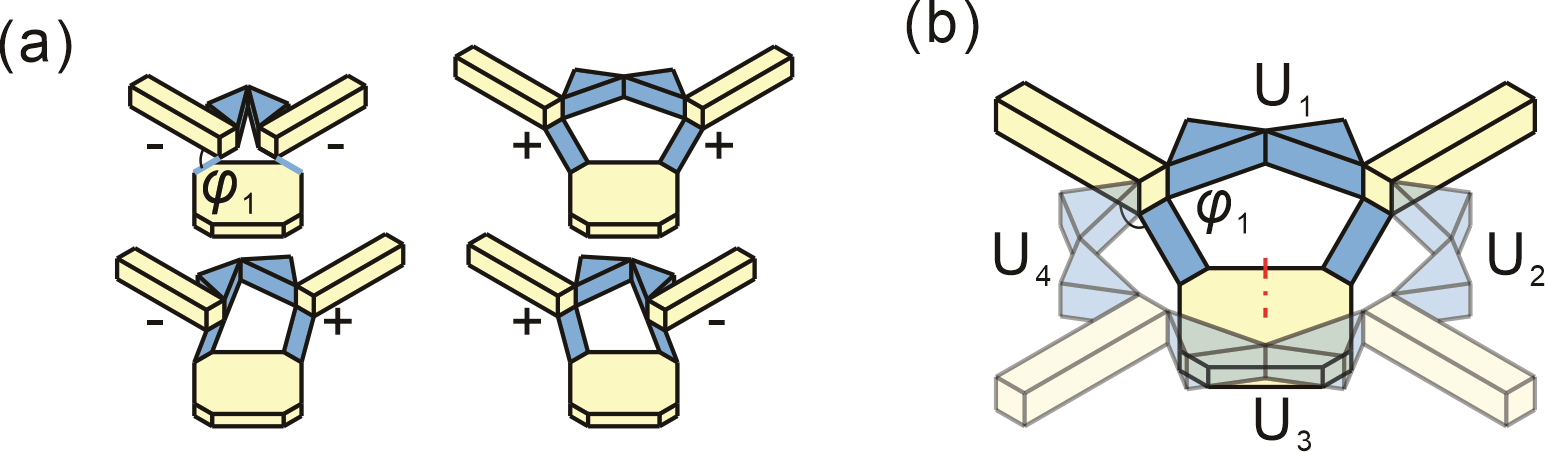
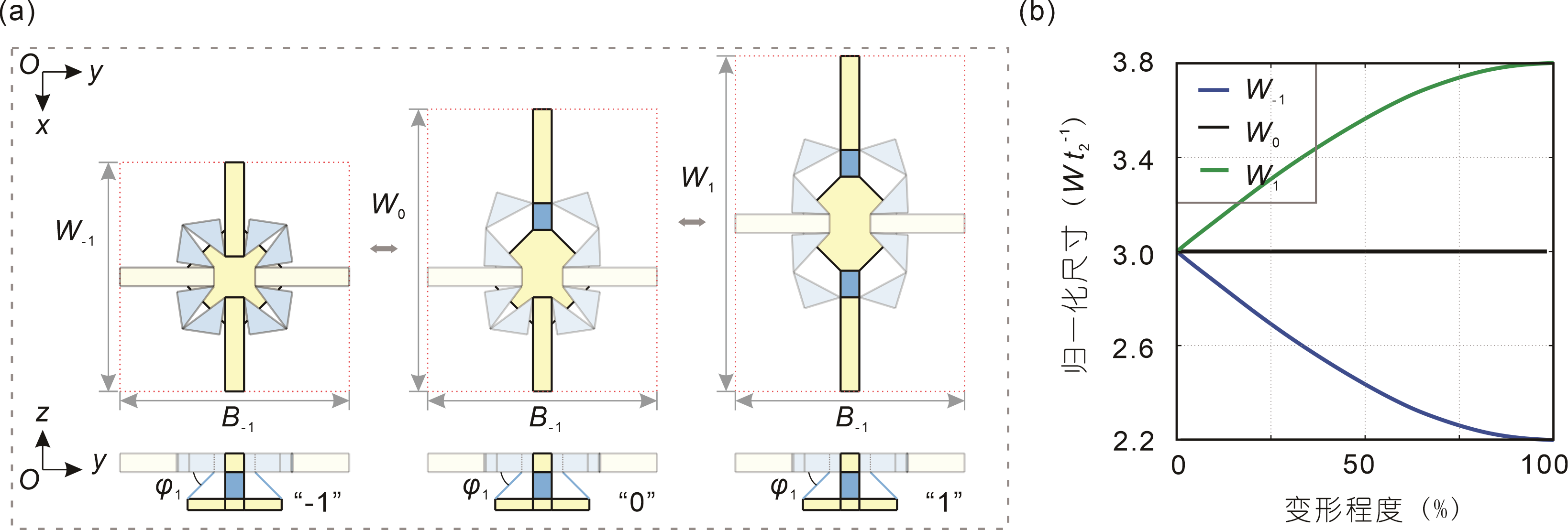
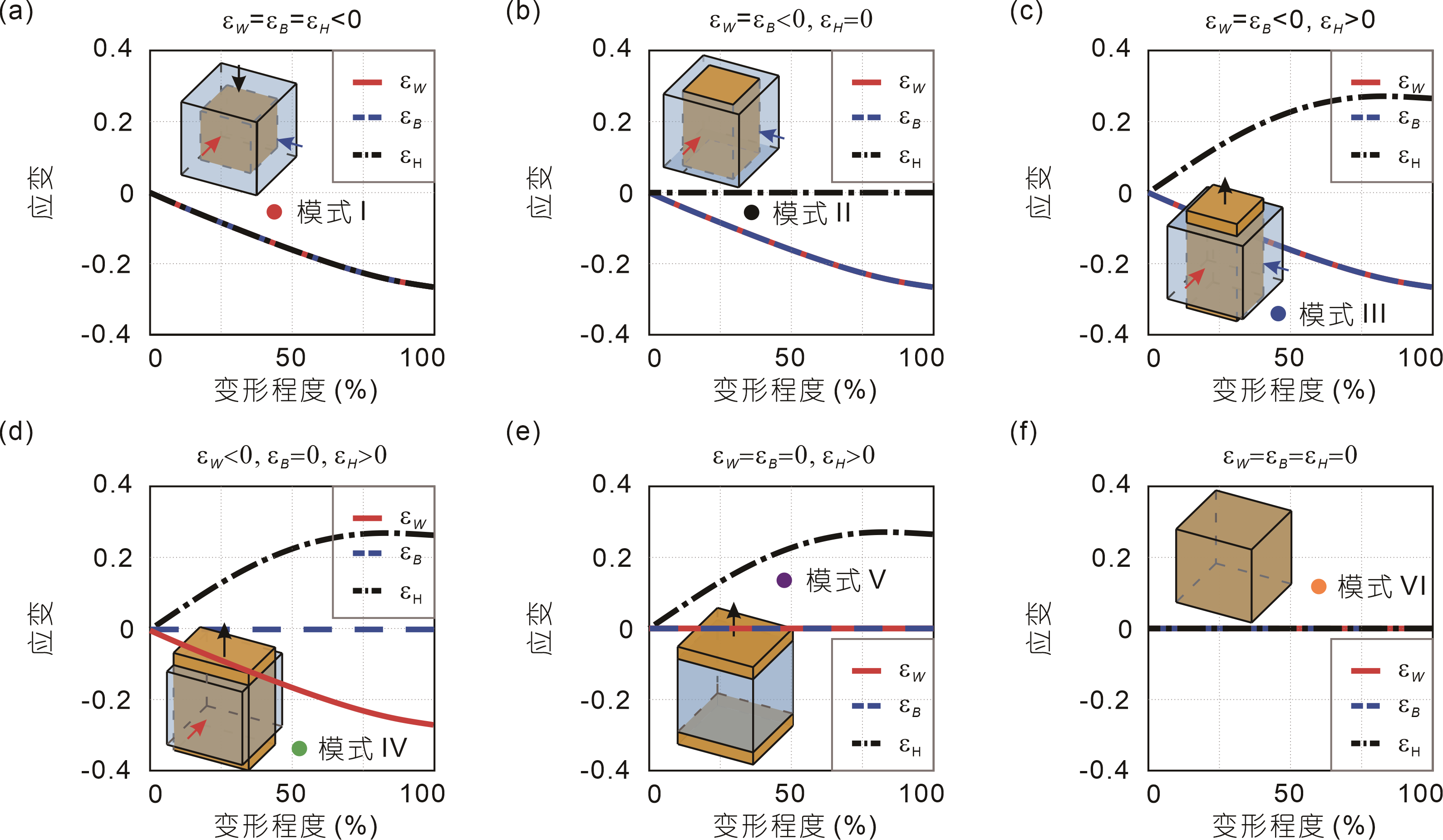
导读

        机械超材料通过精心设计的微观或宏观结构单元获得超越传统材料的力学响应（如负压缩性、多稳态以及压扭耦合等），展现了“构型主导性能”的全新材料设计范式。其中，泊松比作为表征横向变形响应的关键指标，对材料的吸能、波传播等性能至关重要。目前，研究人员已通过内凹蜂窝结构、手性单元和折/剪纸结构等多种设计策略，成功构建了具有固定泊松比符号的超材料体系。在此基础上，在单一结构中实现逆转横向应变方向的泊松比符号可切换超材料，成为该领域的研究热点，并在自适应减振、可调带隙器件及智能传感等领域展现出巨大应用潜力。然而，现有的泊松比符号可切换超材料仍局限于二维体系，其应变方向反转通常仅发生在平面变形模式中。即便是名义上的三维设计，正交方向的变形自由度通常存在耦合，难以实现多方向应变的独立编程。目前，如何在单一结构体系内实现泊松比的连续全谱覆盖仍是一项挑战，因为这不仅要求在数值上实现从负到正的跨越，还需要涵盖沿各主方向的（收缩、零应变和膨胀）全部变形模式。

        近日，天津大学陈焱教授团队提出了一种基于正交解耦运动学的可重构模块化折纸超材料，通过数字化编码策略，在单一结构中实现了泊松比全谱响应的自由切换。相关成果以“泊松比全谱编程的可重构模块化折纸超材料”为题，于2025年12月18日作为邀稿论文在线发表于《中国科学: 物理学 力学 天文学》。论文通讯作者为天津大学陈焱教授，第一作者为刘伟奇助理研究员。马家耀教授对研究工作给予了重要指导和支持。该研究由国家自然科学基金、国家重点研发计划“智能机器人”重点专项、腾讯基金（科学探索奖）资助完成。

        该研究的设计灵感源于一种具有运动分岔特性的空间连杆机构。研究人员将其几何参数系统性映射到相应的折纸构件（矩形面板、三角形面板及八棱柱基座）中，赋予了折纸单元与原机构一致的单自由度特性与丰富的运动分岔特征。如图1所示，单元具有多条运动分支：沿 M1 路径运动时，可实现对称收缩（-, -）或对称膨胀（+, +）；沿 M2 路径演化时，则呈现出反对称混合状态 (-, +)与 (+, -)。

图1 由四个相同的基础单元围绕中心垂直轴组装成的二维模块

        为了将单个单元的可重构性扩展到功能性材料系统，四个相同的单元U₁-U₄围绕中心垂直轴组装成一个闭合模块。由于模块具有四重旋转对称性，其分岔点重合并同步演化，使得系统的面内变形呈现出独特的正交解耦特性。如图 2 所示，每个方向均可呈现三种变形状态：当对应的两个矩形面板均向基座方向摆动时，该方向尺寸W_-1随变形单调减小，表现为收缩状态；当两个面板的运动趋势相反时，几何效应相互抵消，尺寸W₀保持不变，形成零应变状态；当两个面板均远离基座方向摆动时，该方向尺寸W₁随变形增加，表现为膨胀状态。为对上述三类宏观变形进行统一表征，引入了一种数字化应变状态编码方案：沿 x 方向的响应记为S_x∈{-1, 0, +1}，沿 y 方向的响应记为S_y∈{-1, 0, +1}，其中 -1, 0，+1, 分别对应收缩、零应变和膨胀三种应变响应。由于两对矩形面板的运动在运动学上是解耦的，模块的整体面内变形状态可表示为二者的组合 C_{(Sx, Sy)}。

图2 2D模块的正交解耦变形状态

        基于数字化编码策略，二维模块的构型空间被归纳为四种代表性的变形模式，如图3所示：

图3 2D模块的四种代表性变形模式

        模式I对应模块从分岔构型⑨到完全收缩构型①或完全膨胀构型⑤的连续变形。在该模式中，两主轴方向的应变具有相同符号且幅值一致，如图4(a) 与图4(b) 所示，导致泊松比保持恒定为 −1，表现为典型的负泊松比行为。在模式II中，模块由构型⑨转变到构型②或构型⑥，变形仅沿单一主方向发生，而正交方向的尺寸保持不变。如图4(c)和4(d)所示，该模式对应零泊松比响应。模式 III 发生于模块由构型 ⑨ 向构型 ③ 或构型 ⑦ 的变形过程中。该模式下，两主方向应变符号相反，即一个方向收缩而另一个方向膨胀。图4(e) 与图4(f) 中的应变曲线表明，该模式对应正泊松比行为，体现常规材料特征。相较之下，模式IV对应模块从构型 ⑨ 向构型 ④ 或构型 ⑧ 的变形过程。在此模式中，两主方向的应变均为零，如图4(g) 与图4(h) 所示，模块整体尺寸保持不变，内部构件仅发生几何重新排布，而不引入宏观尺度变形。综上，以二维模块为胞元的超材料能够在面内泊松比的全谱响应范围内进行重构，展现出从各向同性到高度各向异性的负值、零值和正值之间切换的泊松比调控能力。

图4 2D模块四种代表性变形模式下的应变响应

         利用L型连杆连接六个二维模块，研究进一步构建了三维立方体超材料（图5）。理论分析表明，该结构拥有27种运动学兼容构型，归纳为六种代表性变形模式（图6），分别对应C_{(-1, -1, -1)}, C_{(-1, -1, 0)}, C_{(-1, -1, 1)}, C_{(-1, 0, 1)}, C_{(0, 0, 1)}, 和 C_{(0, 0, 0)}。每种模式对应着三个主方向上特定编码状态的组合，从而实现对全局变形行为的编程调控。

图5 三维立方体超材料构造示意图

图6 立方体超材料的构型空间及其六种代表性的变形模式

         如图7(a)所示，在模式 I 中，C_{(-1, -1, -1)} 构型超材料在三个主方向上均匀收缩，表现为完全各向同性的负泊松比。模式 II对应图7(b)中 C_{(-1, -1, 0)} 构型。超材料在xoy平面内保持负泊松比，而z方向的变形为零，呈现出零泊松比特性。而在图7(c)所示的模式 III中，C_{(-1, -1, 1)} 构型超材料在面内保持负泊松比的同时，在面外表现出如常规材料般的正泊松比行为。在图7(d)所示模式 IV 中，C_{(-1, 0, 1)} 构型超材料三个主方向的应变符号分别为负、零、正，展现出高度各向异性。在图7(e)所示模式 V 中，C_{(0, 0, 1)} 构型超材料实现了纯粹的一维变形，应变仅沿z轴发生，形成可编程的单轴材料。图7(f)中的模式 VI 则体现了内部运动学与宏观变形的完全解耦，超材料在所有全局尺寸恒定的前提下实现了纯内部重构。上述六种模式覆盖了从完全各向同性到高度各向异性的全谱泊松比响应。

图7 立方体超材料六种代表性变形模式下的应变响应

         除了力学性能的可编程，研究人员通过在关键连接处集成双金属片驱动铰链，利用金属热胀冷缩的特性差异，研究人员成功将环境热能转化为驱动力。实验表明（图8），当温度从20°C升至140°C时，该超材料能根据预设的“程序”展现出正热膨胀（受热膨胀）或负热膨胀（受热反而收缩）的特性。

图8 集成双金属片驱动铰链的2D模块的热响应

        综上所述，该研究提出了一类具有正交解耦运动学的可重构模块化折纸超材料，实现了泊松比的可编程调控，涵盖了理论上的完整泊松比谱。该研究以分岔重构机构为几何引擎，建立了几何构型与力学响应、乃至热学性能的物理映射，为可编程力热耦合超材料的开发提供了全新视角，在航空航天变体结构及软体机器人等领域展现出广阔的应用潜力。

刘伟奇, 马家耀, 陈焱*. 泊松比全谱编程的可重构模块化折纸超材料, 中国科学:物理学 力学 天文学. (https://doi.org/10.1360/SSPMA-2025-0510)