|
最新论文——International Journal of Mechanical Sciences | 柴思博同学发表曲纹折纸的面板驱动机制
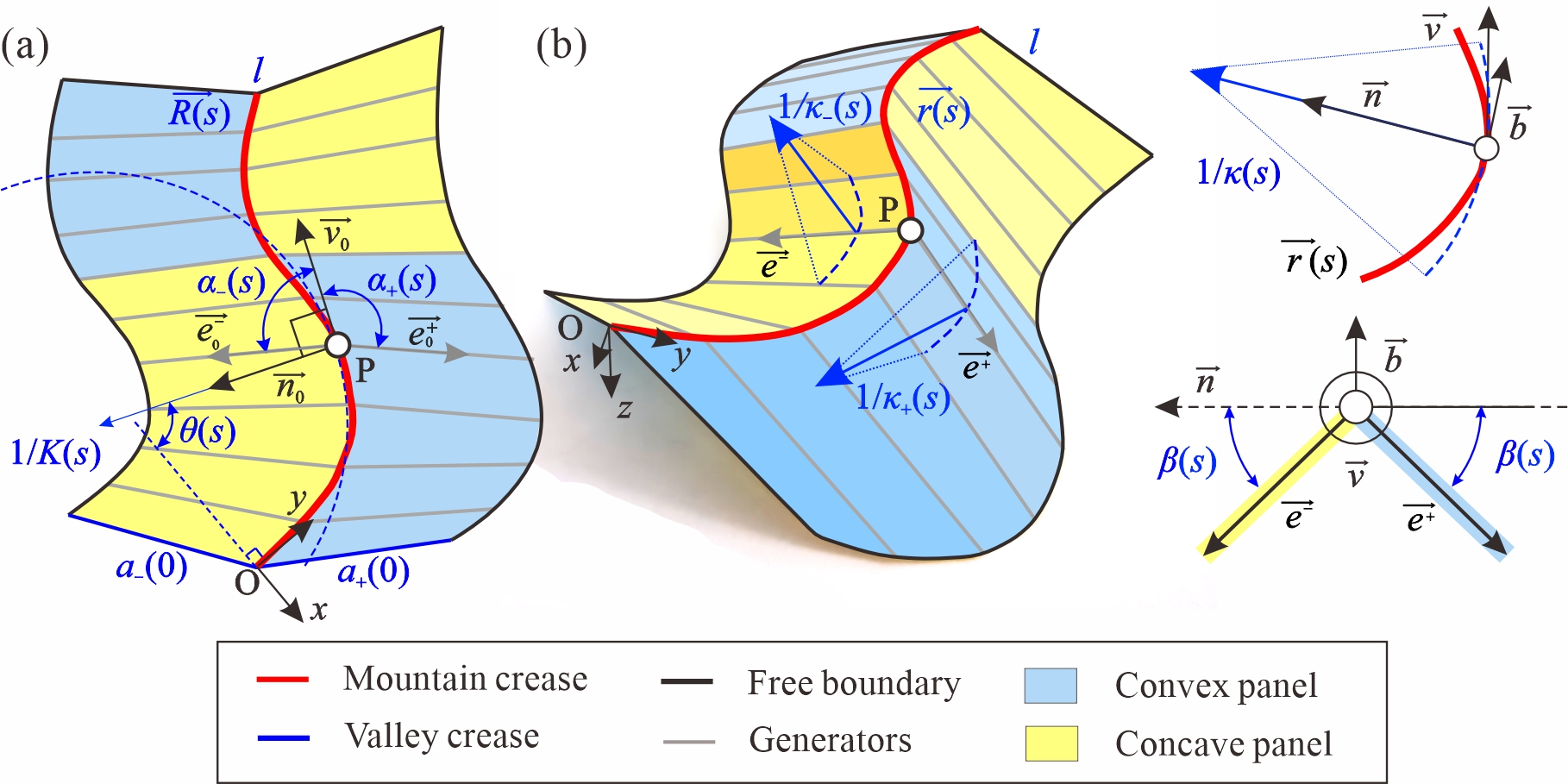
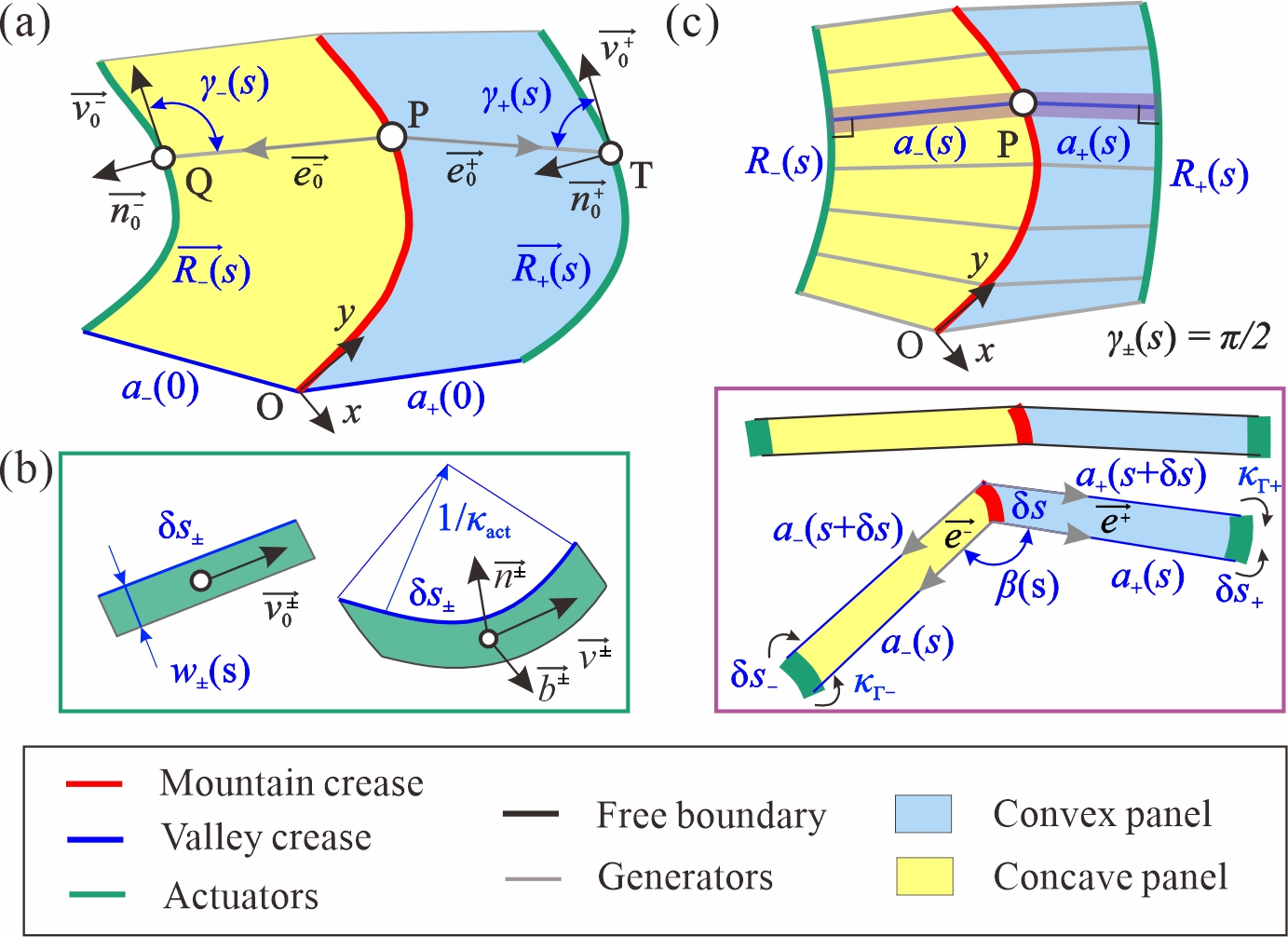
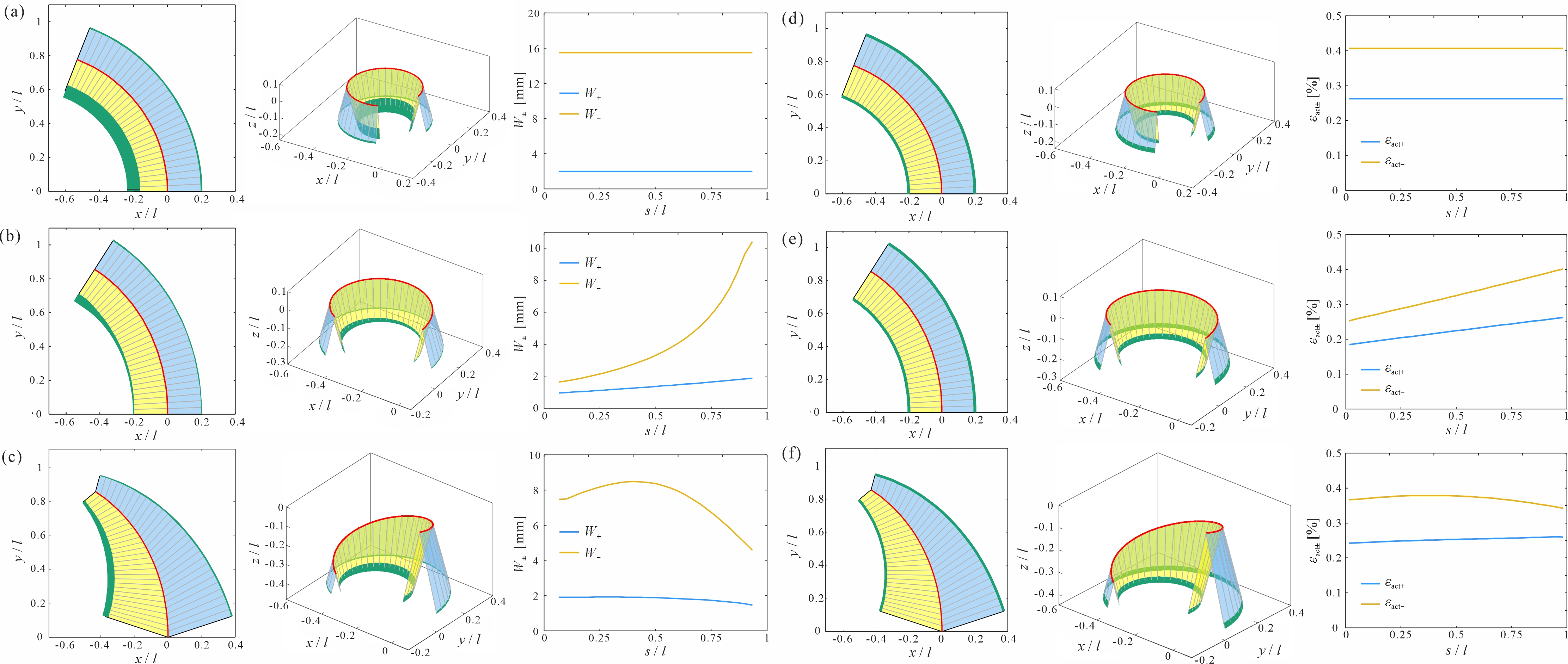
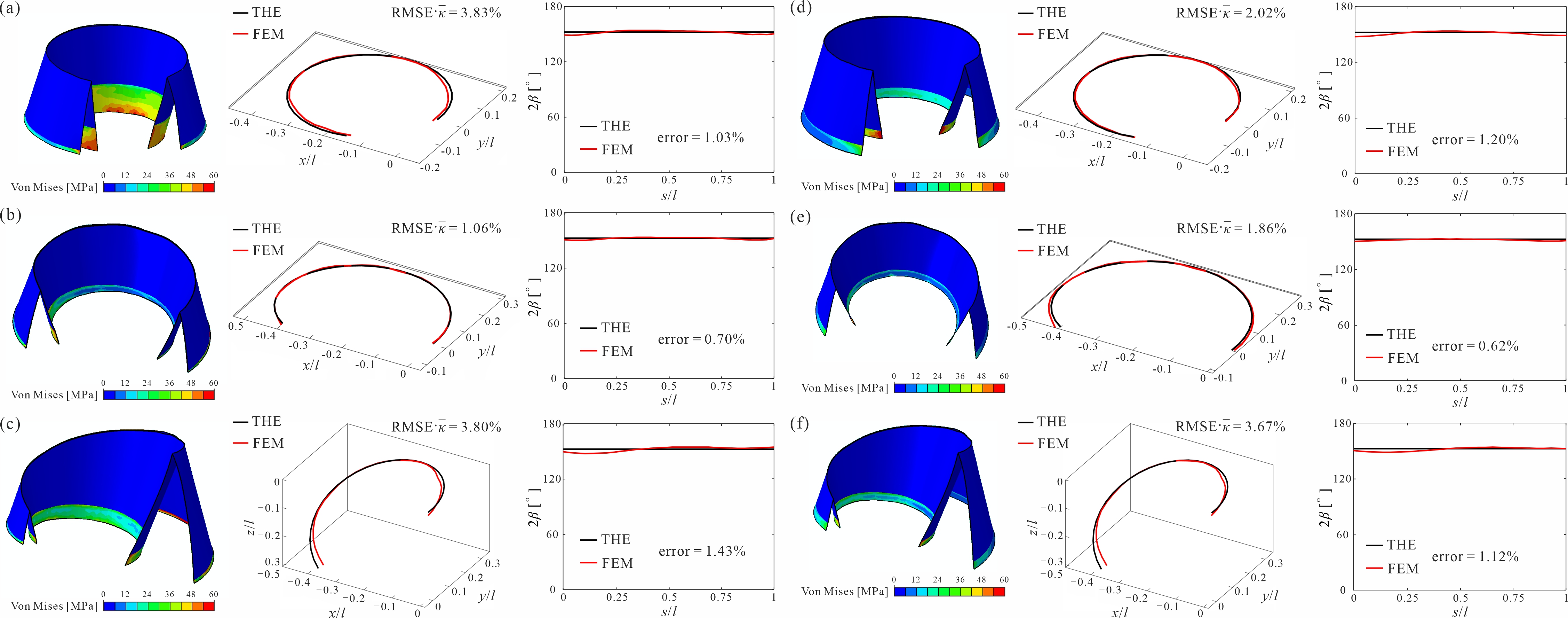
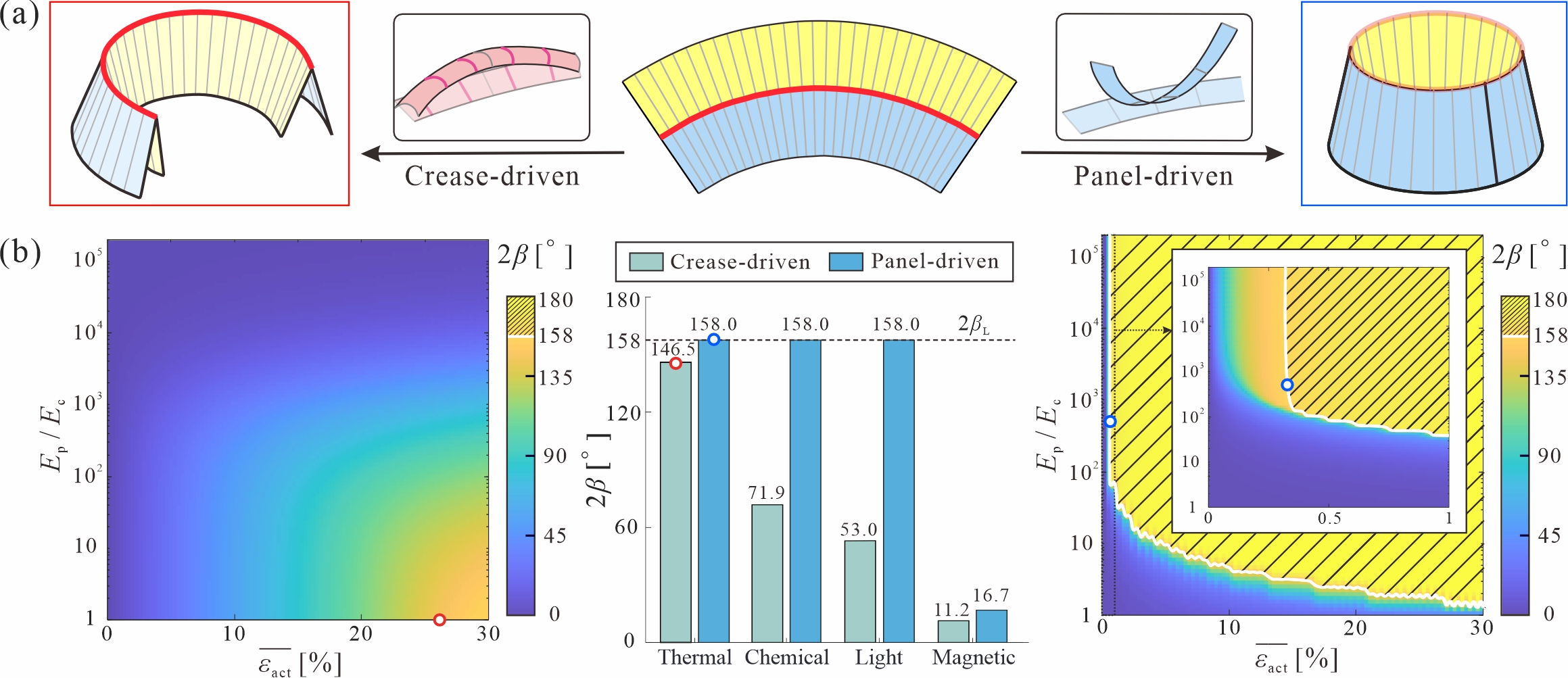
From: Date: 2026-02-09 曲纹折纸是非刚性折纸的一种特殊形式,其特点在于面板沿曲线折痕折叠的同时发生弯曲变形。与直纹折纸相比,曲纹折纸通过引入折痕的固有曲率拓展了设计空间,能够实现形状编程、刚度调控、能量吸收以及隔振等多种功能特性。然而,从平面图案到功能性三维构型的可控转换,仍需有效的驱动方法来实现。传统驱动方法将环境响应材料置于折痕处,通过诱导折痕弯曲来驱动结构的整体折叠。该方法虽能有效驱动直纹折纸,但由于折痕区域狭窄,其所能提供的扭矩不足以克服曲纹折纸面板的弯曲变形,导致驱动效率不足。此外,如何通过主动驱动实现从单一平面图案到复杂三维目标构型的可编程变形,尤其是对于偏离自然能量最小路径的折痕扭转变形,仍然是当前研究中的关键挑战。 近日,天津大学马家耀教授团队提出了基于面板变形主导的曲纹折纸驱动机制,确定了驱动条带垂直于母线布置的最优方式,并提出了可编程宽度与可编程应变两种驱动策略,从而实现了曲纹折纸结构的高效自折叠以及对复杂三维构型的精准编程控制。相关研究成果以“Panel-driven actuation framework for curved-crease origami”为题,于2026年2月4日在线发表于International Journal of Mechanical Sciences期刊。论文通讯作者为天津大学马家耀教授,第一作者为博士生柴思博。天津大学陈焱教授和英国牛津大Zhong You教授也为本研究做出了重要贡献。该研究获国家自然科学基金(项目编号:52422502, 52375022, 524B2048, 52192631)资助。 研究团队首先建立了通用曲纹折纸的几何模型与折叠运动学理论框架,系统分析了折痕曲率、母线角度分布等几何参数对结构折叠变形模式的影响(图1)。在此基础上,将弯曲驱动条带集成于折纸面板,通过理论推导证实当驱动条带正交于母线布置时,驱动效率可实现最大化(图2)。为建立驱动参数与折叠构型的定量关系,将曲纹折纸结构离散为有限个折痕-母线单元,通过计算折痕、面板及驱动条带的应变能,基于最小能量原理建立驱动应变与折叠角之间的平衡关系。 图1 通用曲纹折纸的几何建模与折叠运动学 图2 最优驱动布置与面板驱动策略 针对折痕-母线单元沿曲纹方向的驱动参数分布,提出了两种可编程驱动策略。可编程宽度驱动策略,即在保持驱动应变恒定的前提下,通过调控驱动条带的宽度来实现变形编程。可编程应变驱动策略,即固定驱动条带宽度,通过调节驱动应变沿路径的分布以实现目标构型(图3)。基于这两种策略,设计并计算了平面圆弧折痕、平面螺旋折痕以及空间螺旋折痕等多种复杂三维构型的驱动方案。特别是空间螺旋构型,其变形涉及折痕的扭转,偏离了能量最小的自然变形路径,难以通过常规机械加载实现,展现出面板驱动方法在实现复杂变形模式方面的独特优势。 图3 可编程宽度与可编程应变的驱动策略 为验证面板驱动机制的有效性,采用热响应双金属与聚合物组合的方式,制备了可编程宽度驱动策略对应的物理模型,成功实现了三种设计构型的自折叠驱动(图4)。定量分析结果显示,变形后结构曲面与理论目标构型十分吻合,归一化均方根误差均低于10%,充分证实了面板驱动方法的可行性。此外,还通过数值仿真对两种可编程驱动策略下的三个构型进行了模拟(图5)。结果表明变形后的折痕曲线与理论目标的几何偏差小于4%,沿折痕分布的折叠角误差则在2%以内。 图4 可编程宽度驱动策略的实验验证 图5 可编程宽度与可编程应变驱动策略的数值仿真结果 进一步对面板驱动与传统折痕驱动方法的性能进行了系统比较(图6)。结果表明,在实现相同折叠程度时,面板驱动所需的驱动应变比折痕驱动低近两个数量级。具体而言,当模量比大于100时,面板驱动仅需0.3%的驱动应变即可实现自锁构型;而折痕驱动即使在最优模量比条件下,施加高达30%的应变仍难以达到相同构型。这种高效的驱动能力使面板驱动策略能够适用于绝大多数环境响应材料,包括热响应、光响应、化学响应及磁响应材料。此外,折痕驱动方法本质上难以控制折痕的面外变形,因此无法区分折痕曲率相同但母线分布不同的构型(如平面螺旋与空间螺旋构型),从而无法实现对不同曲面构型的驱动编程。 图6 面板驱动与折痕驱动的驱动效率对比 综上所述,本研究提出了一种面向曲纹折纸的面板驱动机制。通过建立通用曲纹折纸的几何模型与折叠运动学体系,通过可编程宽度与可编程应变两种驱动策略,实现了对平面圆弧、平面螺旋及空间螺旋等多种复杂三维构型的精准编程,且所需驱动应变较传统折痕驱动方法降低了近两个数量级。该驱动机制为曲纹折纸的主动折叠与形状编程奠定了理论基础,在隔振、能量吸收、机器人等领域具有广阔的应用前景。
Sibo Chai, Yan Chen, Zhong You, Jiayao Ma*. Panel-driven actuation framework for curved-crease origami. International Journal of Mechanical Sciences, 2026, 313, 111312. |