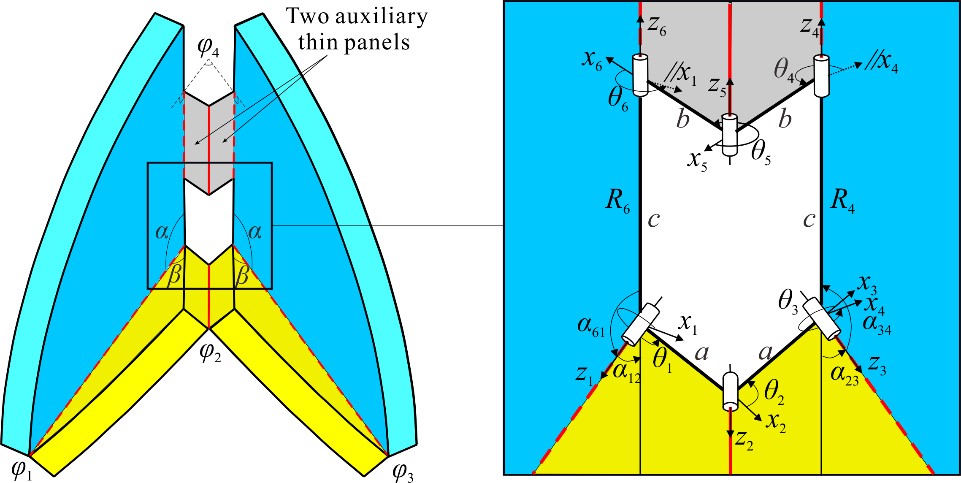
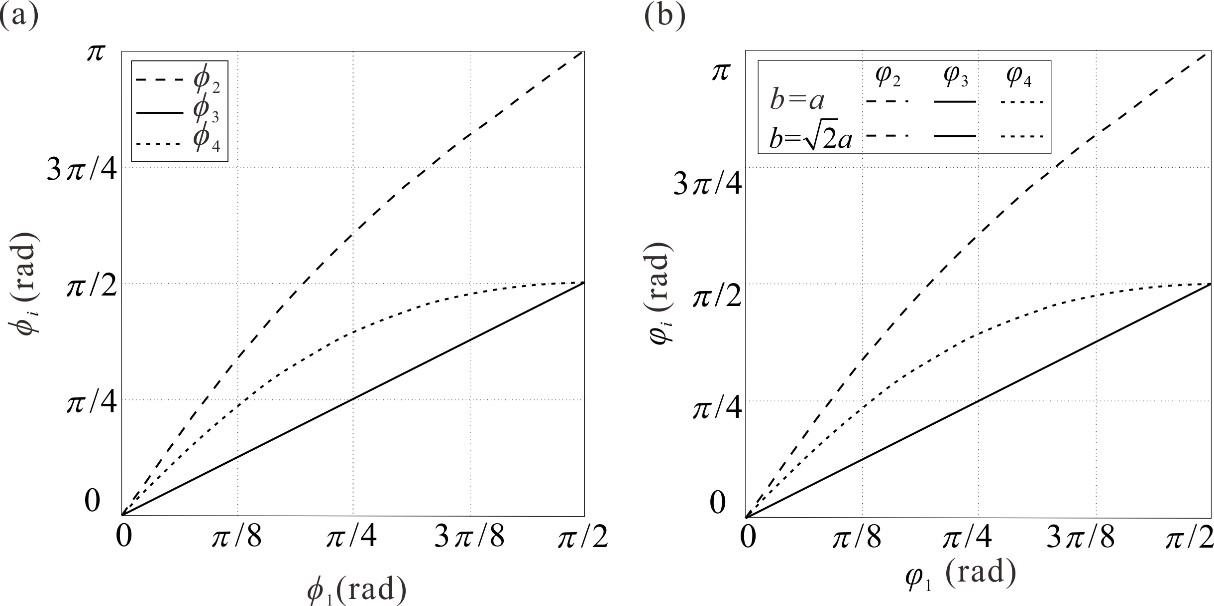
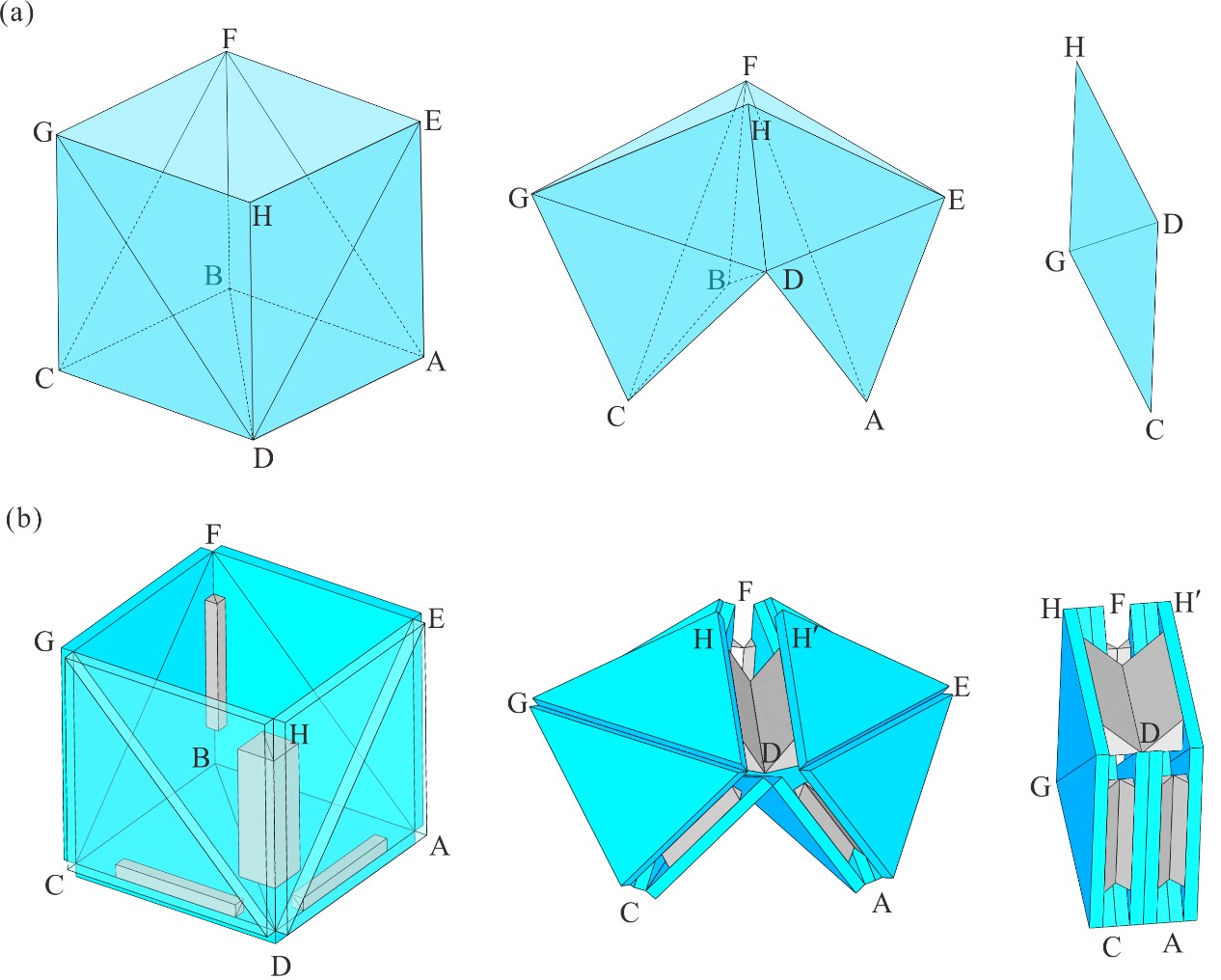
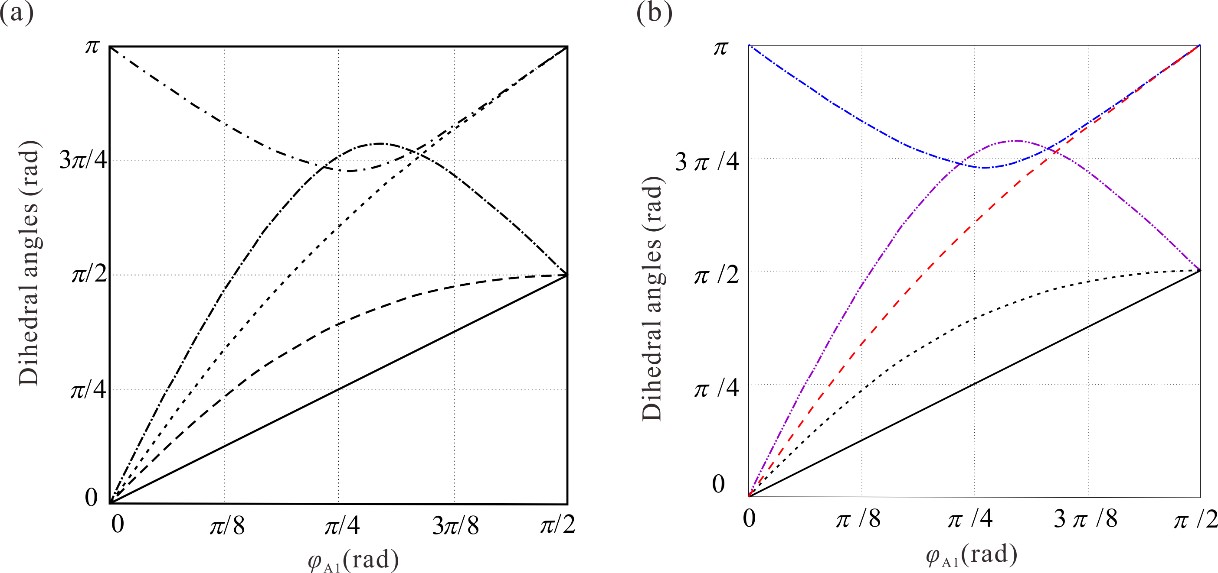
Origami-inspired structures and mechanisms have founded applications in wide areas including robotics, medical devices, mechanical metamaterials and so on. In order to enhance the engineering applications of origami patterns in thick-panel structures, various thickness accommodation methods have been suggested. For example, the equivalent thick-panel form of Miura-ori pattern has been constructed by replacing the spherical 4R linkages in four-crease origami vertices with Bennett linkages. However, the Bennett linkage is not feasible for the thick-panel construction of the general plane-symmetric origami vertex due to its strict geometric constraints. Establishing the novel kinematic model and obtaining the equivalent thick-panel origami vertex and thick-panel origami cube are the main objectives.
        Dr. Yuanqing Gu and Prof. Yan Chen from Department of Mechanical Engineering of Tianjin University and Prof. Guowu Wei from School of Science, Engineering and Environment of University of Salford presented the novel construction method of the general plane-symmetric thick-panel origami vertex by introducing the plane-symmetric Bricard linkage. By solving the closure equations and motion curves of the origami vertex and its thick-panel form respectively, it is verified that the proposed thick-panel vertex preserves kinematics of the original four-crease origami vertex.

The general plane-symmetric thick-panel origami vertex (α+β＜π)and its equivalent Bricard linkage.

Input-output curves of dihedral angles of the (a) general plane-symmetric origami vertex and (b) its thick-panel form.

Folding process of the general plane-symmetric thick-panel origami vertex.

        One-DOF flat foldable thick-panel origami cube was constructed based on the zero-thickness origami cube pattern. By analyzing geometric constraints and closure equation of the corresponding integrated mechanism. it is verified that the motion behavior of the cube in the above two construction forms is consistent, as shown in the two sets of motion curves below, which reveals their kinematic equivalence between the thick-panel and zero-thickness forms of this origami cube. The advantage of the above equivalent property is that the known kinematics of zero-thickness origami can be utilized to directly control and plan its thick-panel motion.

(a) Zero-thickness origami cube and (b) its thick-panel form

Input-output curves of dihedral angles of the (a) zero-thickness origami cube and (b) its thick-panel form

        This work was accepted by Mechanism and Machine Theory on May 27, 2021 and published online on June 15. The new method can be readily extended to transfer the zero-thickness origami patterns into its thick-panel counterpart, which provides great convenience for the direct application of rich origami patterns in art and mathematics, and provides a new idea and theoretical basis for the subsequent innovative design of thick-panel origami.

Yuanqing Gu, Guowu Wei, Yan Chen, 2021, Thick-panel origami cube, Mechanism and Machine Theory, Volume 164, 104411.
(https://doi.org/10.1016/j.mechmachtheory.2021.104411)