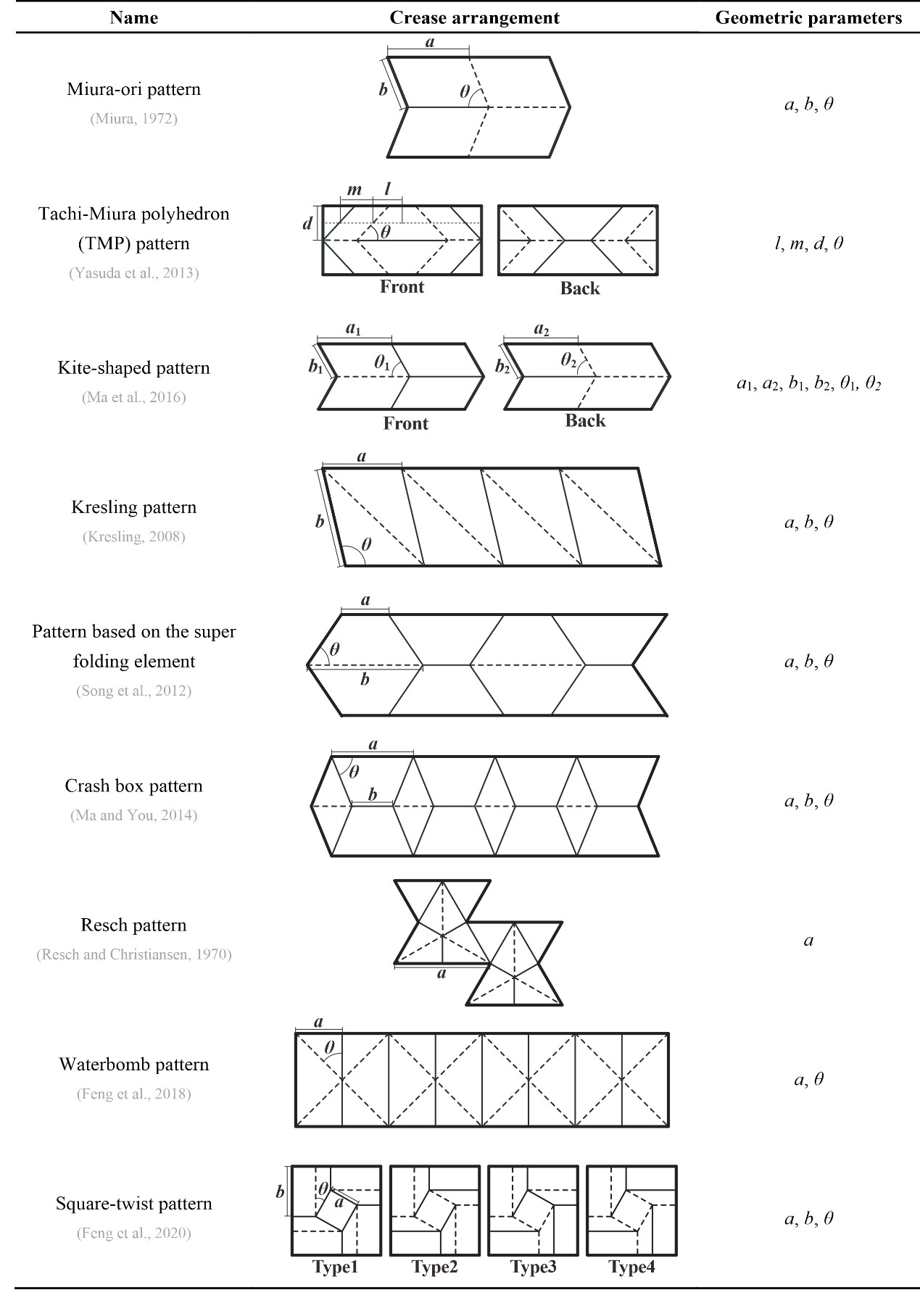
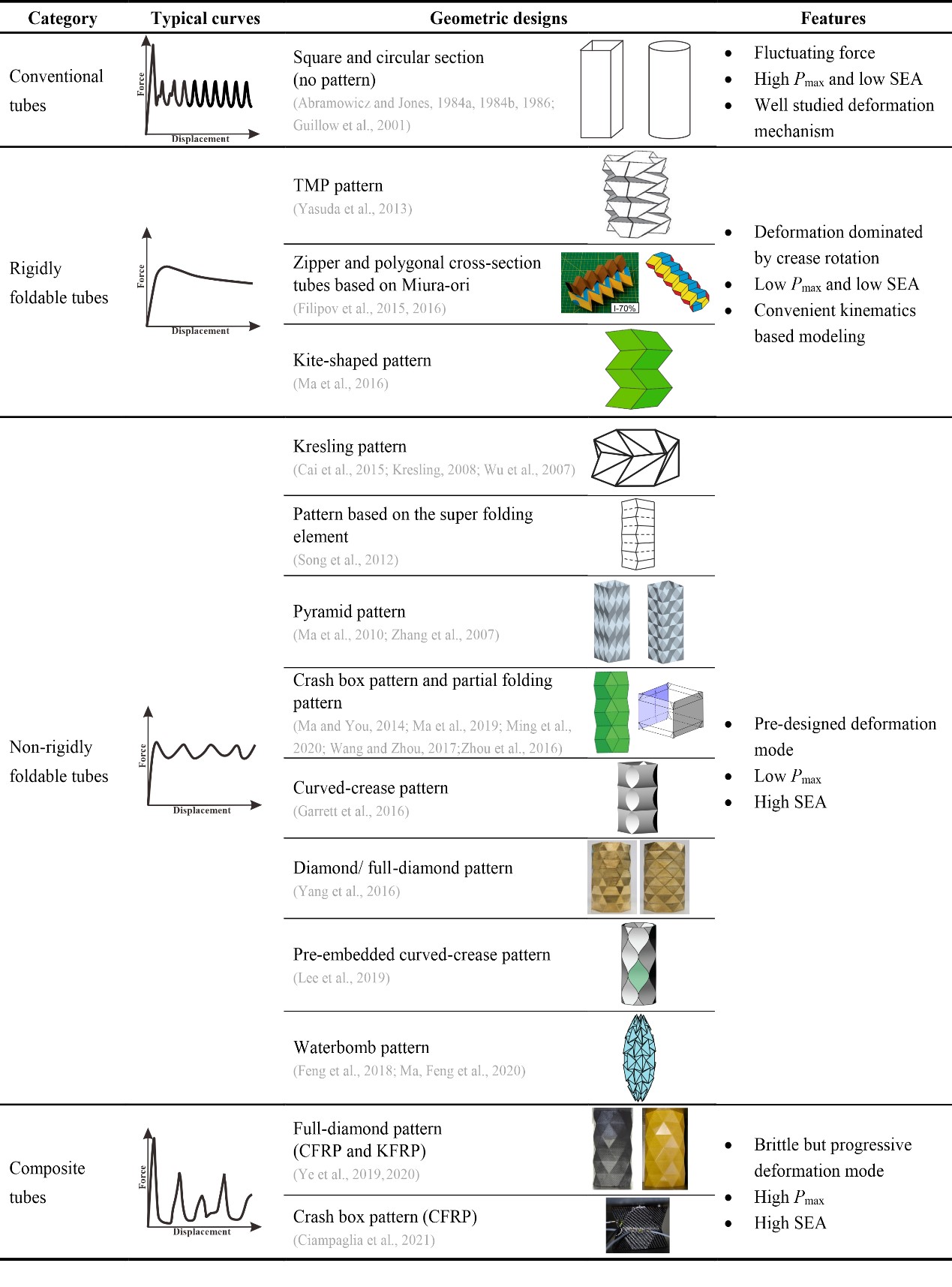
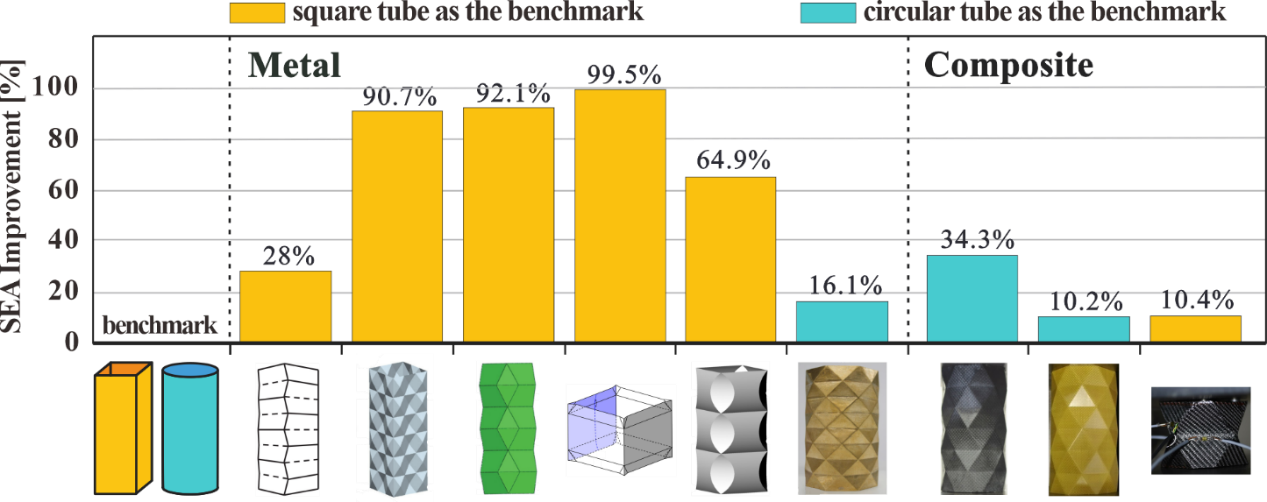
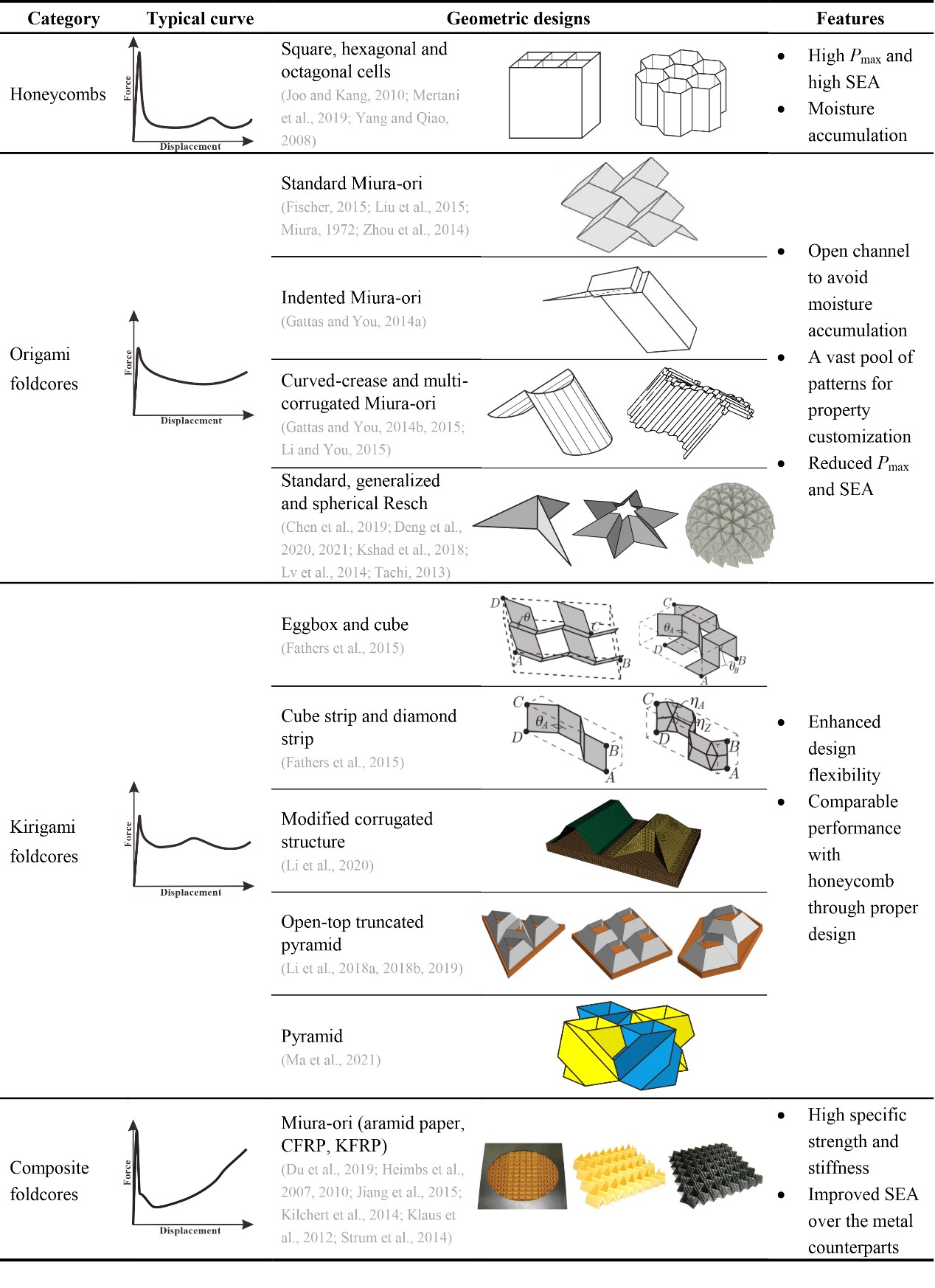
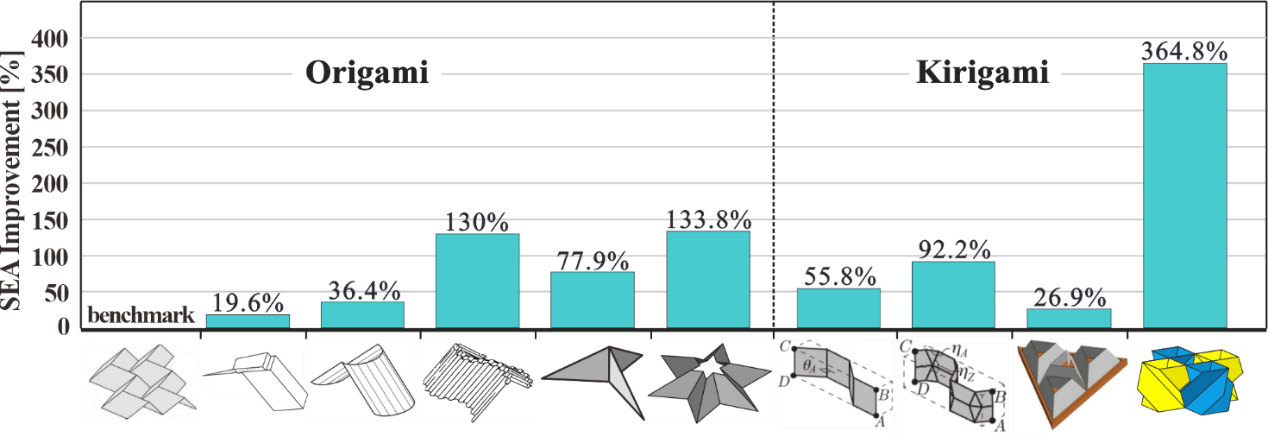
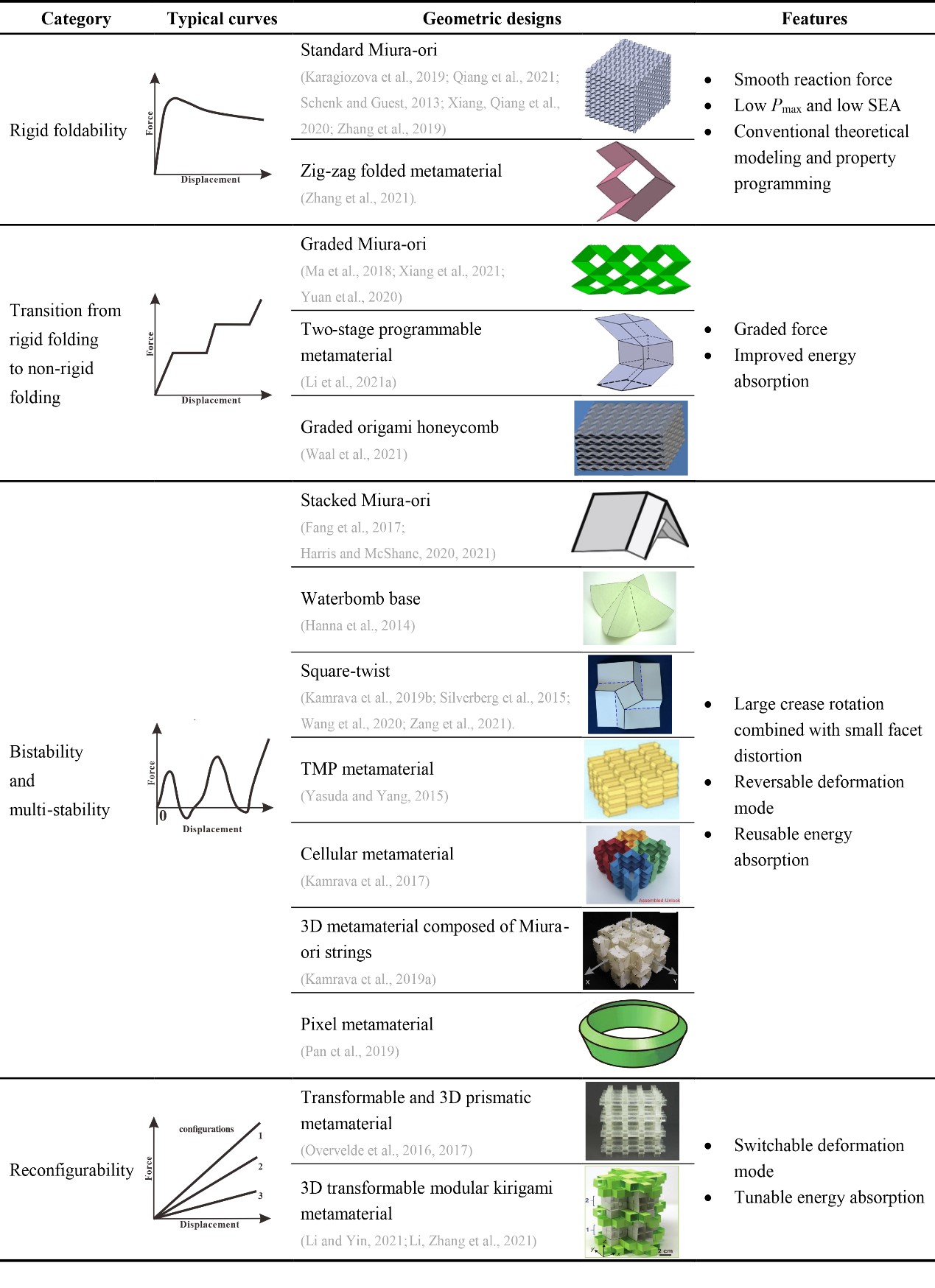
Thin-walled structures have been widely applied as energy absorption devices due to their lightweight, high energy dissipating capability through large deformation, and low cost. Nowadays energy absorption devices are of paramount importance in various fields from aviation to vehicles and civil engineering (Fig. 1). The mechanical behavior of a structure is expected to have a low initial peak force, steady and large deformation progress, and most importantly a high energy absorption per unit mass. Researchers have pre-folded traditional energy-absorbing structures inspired by origami or kirigami (Table 1), improved their energy-absorbing characteristics by controlling the collapse deformation mode, which formed a research hotspot.

        Recently, invited by Mechanics of Materials, Associate Professor Ma Jiayao, Dr. Chai Sibo and Professor Chen Yan from School of Mechanical Engineering, Tianjin University wrote a review article on patterned thin-walled structures and metamaterials, discussing the geometry design, deformation mode and energy absorption characteristics of patterned tubes, sandwich cores and metamaterials in detail. The main results and limitations of existing research are summarized, and the future development direction is pointed out.

Fig. 1 Some applications of energy absorption structures

Table 1 Summary of origami patterns

Patterned tube in one-dimension

        Researchers have designed many patterned energy absorption tubes with origami patterns, to solve the problems of the high initial peak force and the fluctuation of the force curve of traditional tubes. According to the deformation mode of patterned energy absorbing tubes, the authors divide them into rigidly foldable origami tubes and non-rigidly foldable origami tubes

        Rigid foldable tube refers to that the panel of the tube rotates around the crease with almost no bending deformation in the folding process and the crease formed a fixed plastic hinge for energy absorption. Therefore, the initial peak force is greatly reduced, the deformation mode can be well controlled, and the kinematics of the mechanism and plastic mechanics can be effectively modeled. But at the same time, the energy absorption efficiency of rigid foldable tubes is much low because the deformation is mainly concentrated in the creases (such as TMP origami tubes).

        Non-rigid foldable tube will allow the rotation around the crease and deformation of the panel at the same time, so it could not satisfy the kinematic theory of the mechanism. Besides the fixed plastic hinge deformation formed by creases, there are also movable plastic hinges and in-plane deformation in the energy absorption mechanism. Therefore, non-rigid foldable tubes not only have the advantages of controllable deformation mode and a low initial peak force of rigid foldable tubes, but also greatly improve the energy absorption (such as Crash box structure).

        Besides, a summary of the existing origami tubes grouped by their folding modes and materials is given in Table 2, and the SEA improvement of the non-rigidly foldable tubes in comparison with the corresponding conventional ones is presented in Fig. 2

Table 2 Summary of origami tubes

Fig. 2 The SEA improvement of the non-rigidly foldable origami tubes in comparison with the corresponding conventional tubes

Patterned foldcore/sandwich in two-dimension

        Different from origami tube, patterned foldcore could only fold in non-rigid foldable mode because the upper and lower panels limit the movement of core. According to the design and manufacture method, the folding core can be divided into two types: origami foldcore and kirigami foldcore.

        The foldcore based on origami, represented by the Miura-ori foldcore, has solved the problem of moisture accumulation due to the open channel compared with the traditional honeycomb, and effectively reduced the initial peak force as well. However, the deformation of Miura-ori is mainly reflected in the folding of the locally fixed plastic hinge, so the energy absorption efficiency is very limited. The researchers improved the energy absorption by improving its structures, such as the curved Miura-ori foldcore, and finding new origami patterns, such as the Resch foldcore.

        The foldcore based on kirigami has a wider design because it allows material cutting and bonding based on foldcore, which forms more plastic hinges and more complex in-plane deformation in the deformation, to achieve more efficient energy absorption. Some of these structures can achieve energy absorption close to or even higher than honeycomb (pyramid foldcore, for example).

Table 3 Summary of origami and kirigami foldcores/sandwiches

Fig. 3 The SEA improvement of the origami and kirigami foldcores/sandwiches in comparison with the standard Miura-ori

Patterned metamaterial in three-dimension

        Although many patterned metamaterials are not focused on energy absorption, some of them still exhibit valuable energy absorption properties. The potential of metamaterials in energy absorption is discussed in detail from the following aspects by the authors.

        Rigid foldable metamaterials have low initial peak forces and smooth energy absorption curves and can be effectively theoretically modeled using plastic hinge theory (Miura-ori metamaterials, for example). Some studies have realized the transition from rigid folding to non-rigid folding through the interlayer design of graded geometric parameters or the combination of different structures, and have obtained the gradient characteristics of energy absorption curves while greatly improving the energy absorption (graded Miura-ori metamaterials, for example). The authors point out that the rigid folding mode and the non-rigid folding mode both have their advantages, and the relatively balanced and even superior performance can be achieved if the two modes are combined.

        Bistability and multi-stability are also important research aspects of metamaterials. The state conversion dissipates and stores a lot of energy, and the deformation process is more elastic and recoverable. Thus, bistable or multistable patterned metamaterials can be reused in energy-absorbing devices (such as stacked Miura-ori metamaterials).

        Reconfigurable metamaterials can adapt to different environments and perform different tasks through configuration transformation. Different configurations of the same structure have significant differences in deformation modes and energy absorption, so the reconfigurable metamaterials can realize the transformation and regulation of energy absorption characteristics, and have a wide application prospect.

        The author also summarizes the patterned metamaterials (Table 4) and points out that new multifunctional metamaterials with energy absorption have great research potential.

Table 4 Summary of patterned metamaterials

Challenges and Prospects

        Finally, the research status, challenges and possible solutions of patterned thin-wall energy-absorbing structures are presented from three aspects (Fig. 4).

        The first challenge is the design theory. There still lacks a systematic approach to invent new patterns for energy absorption purposes. On one hand, past studies on the energy dissipation mechanisms such as traveling plastic hinges and in-plane stretching can provide useful guidelines for the generation of folding mode and sequence. Moreover, the recent progress in bio-inspired structures with excellent mechanical performances could inspire the discovery of new deformation modes. On the other hand, the advance in rigid origami theory is expected to facilitate the invention of patterned patterns. Building up on the knowledge of design methodologies, artificial intelligence may be utilized to push the design of patterned structures toward an autonomous reverse design process that can directly compute a pattern based on specific engineering requirements.

        The second challenge is theoretical characterization. The development of analytical models for patterned structures is essential not only to understand the underlying energy dissipation mechanisms but also to set up a relationship between the design parameters and mechanical properties for programmability. The core of theoretical characterization is to obtain a basic folding element that captures the main deformation features of the structure. Classic analytical models for conventional thin-walled structures turned out to be useful references in the study of some patterned structures. Pattern triangulation and the introduction of virtual creases can also be useful in theoretical modeling by turning a non-rigidly foldable pattern into an equivalent rigidly foldable one. For those involving more complicated folding modes, a combination of advanced experimental techniques and numerical simulation would generate extensive data to unveil the deformation evolution process, which can then be integrated with big data mining and data analytics algorithms to produce accurate theoretical models for properties customization and programming.

        The third challenge is the exploitation of advanced materials Advanced composites represented by carbon fiber reinforced materials have high specific stiffness and high specific strength, but their brittle properties lead to fracture and breakage of patterned structures, which could not reflect their performance advantages in plastic deformation mode. Therefore, it is necessary to further study the specific deformation mode and energy absorption mechanism of composites. At the same time, the authors point out that the use of multiple materials in one structure may improve its performance.

        Besides, it is necessary to develop low-cost and mass-produced advanced manufacturing technologies for thin-walled patterned structures, to translate relevant research results into practical engineering applications.

Fig. 4 State of the art, challenges, and possible solutions for the study of patterned energy absorption structures.

Ma J, Chai S, Chen Y. Geometric design, deformation mode, and energy absorption of patterned thin-walled structures. Mechanics of Materials, 2022, 168: 104269.
(https://doi.org/10.1016/j.mechmat.2022.104269)