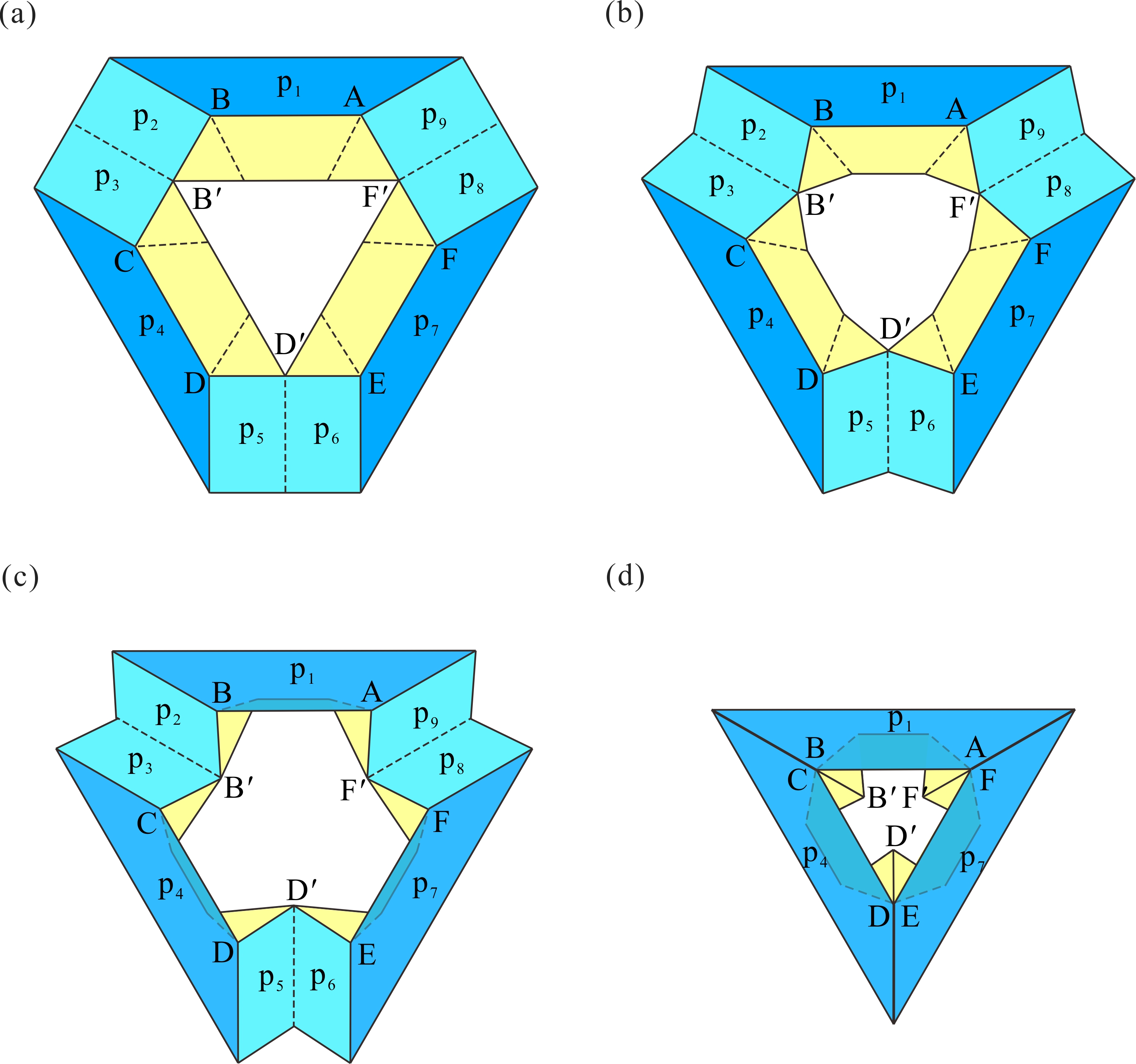
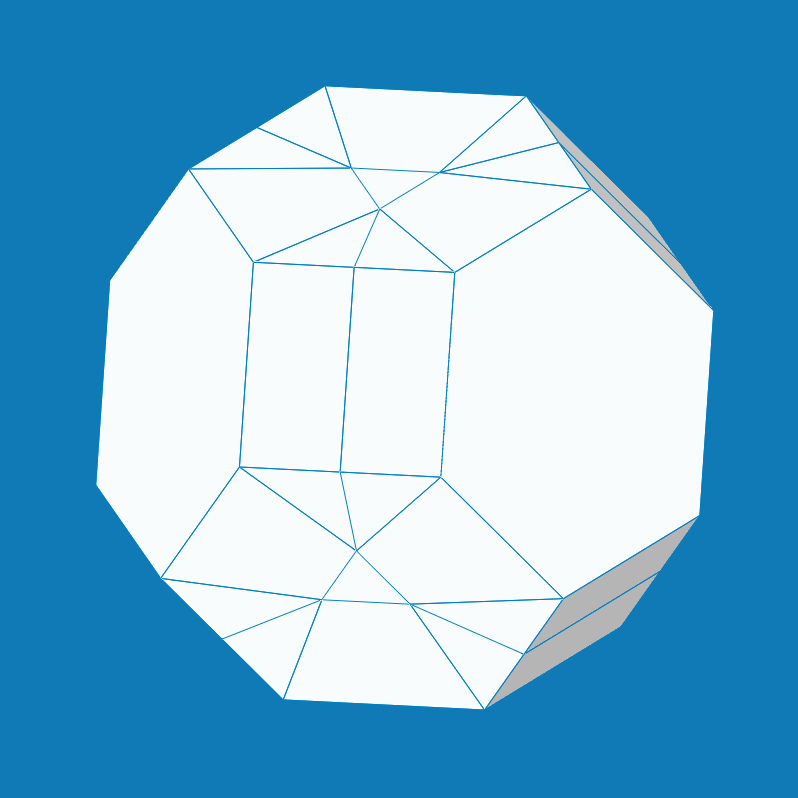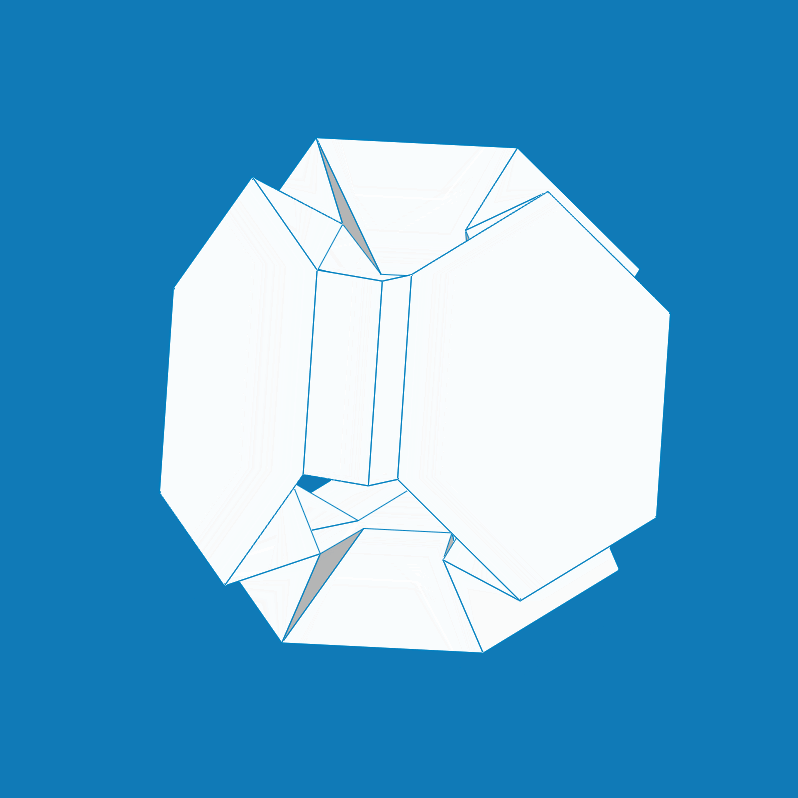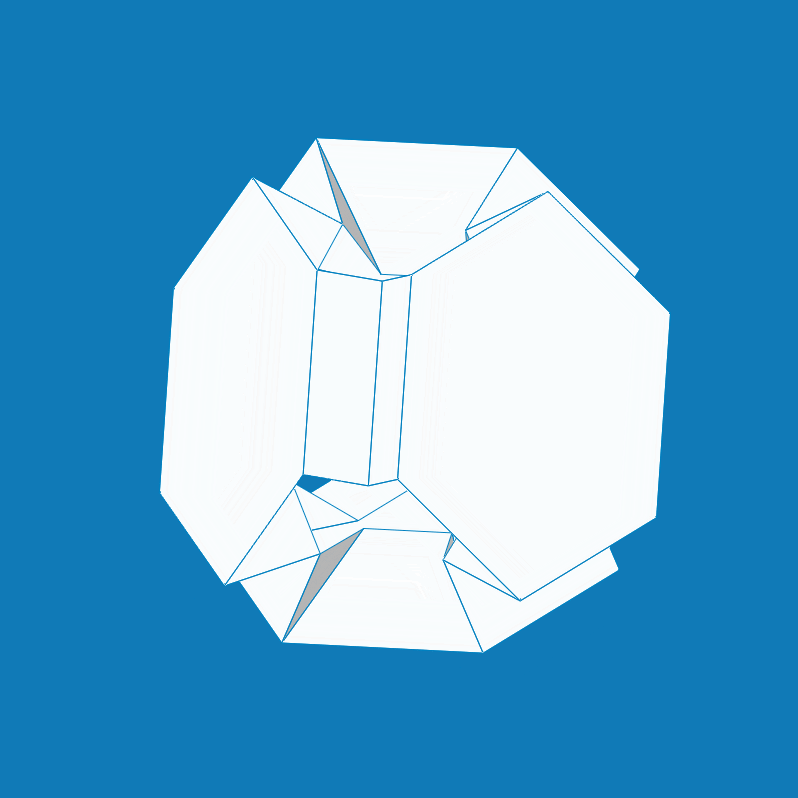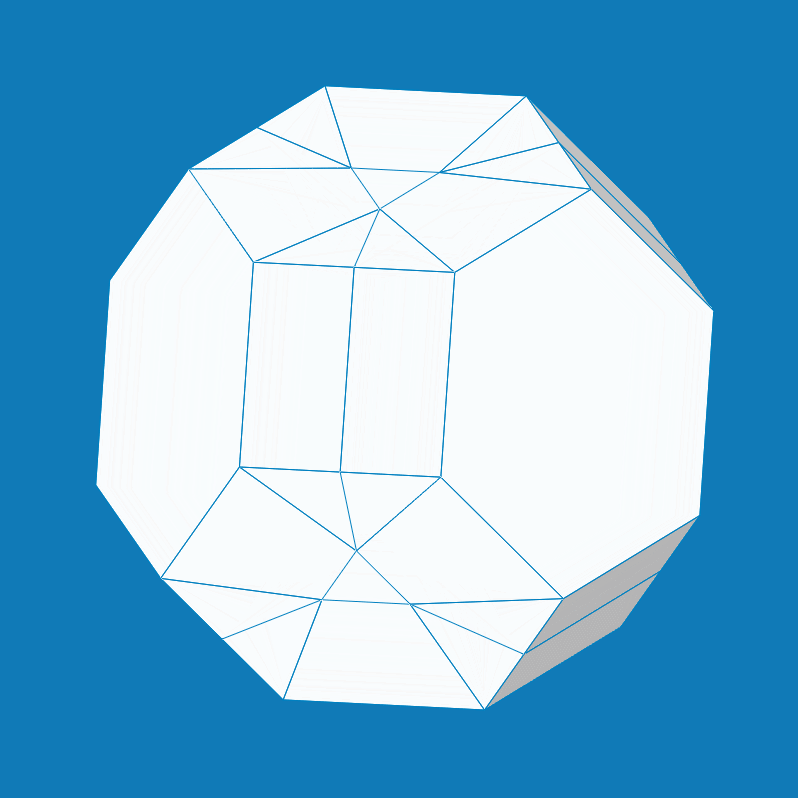
Deployable polyhedrons, especially transformable polyhedrons, are mathematically interesting yet kinematically challenging. Deployable polyhedral mechanisms (DPMs) are generally constructed by embedding linkages and their mobile chains into faces and edges of regular convex polyhedrons. Yet, there is little work on how to construct deployable polyhedrons using the origami mechanism.
        To solve this problem, Ph. D. student Yuanqing Gu and Prof. Yan Chen from Department of Mechanical Engineering of Tianjin University presented an origami-synchronized mechanism with a threefold-symmetric motion feature, and constructed a group of origami polyhedrons with synchronized radial motion, as well as nine polyhedral transformations based on dimensional shortening operations.
        First, a novel origami-synchronized mechanism was constructed by embedding three pairs of S4R linkages (A-B, C-D, E-F) into a spatial 9R linkage (p1-p9) to offer extra motion constraint, in which the synchronized radial motion of three blue platforms (p1, p4, p7) in this origami mechanism was revealed, see Fig. 1.

Fig. 1. Folding process of the origami-synchronized mechanism.

        Regarding the origami-synchronized mechanism as construction cell, the procedure of constructing origami polyhedrons can be summarized as follows. Step 1: divide a threefold-symmetric portion centered on a yellow facet on polyhedral surface according to the corresponding symmetry. Step 2: embed the one-DOF origami mechanism cell into this portion surface. Step 3: synthesize the entire origami polyhedrons following symmetric tessellation of mechanism cells. Thus, a total of three one-DOF origami polyhedral mechanisms can be synthesized in Fig. 2, in which three transformations were obtained during the folding process and each of them retains the original symmetry.

Fig. 2. Three one-DOF origami polyhedral mechanisms. (a) Truncated tetratetrahedron and truncated tetrahedron; (b) truncated cuboctahedron and truncated cube; (c) truncated icosidodecahedron and truncated dodecahedron. Their volumetric expansion ratios are 4.17, 3.07, and 2.43, respectively.

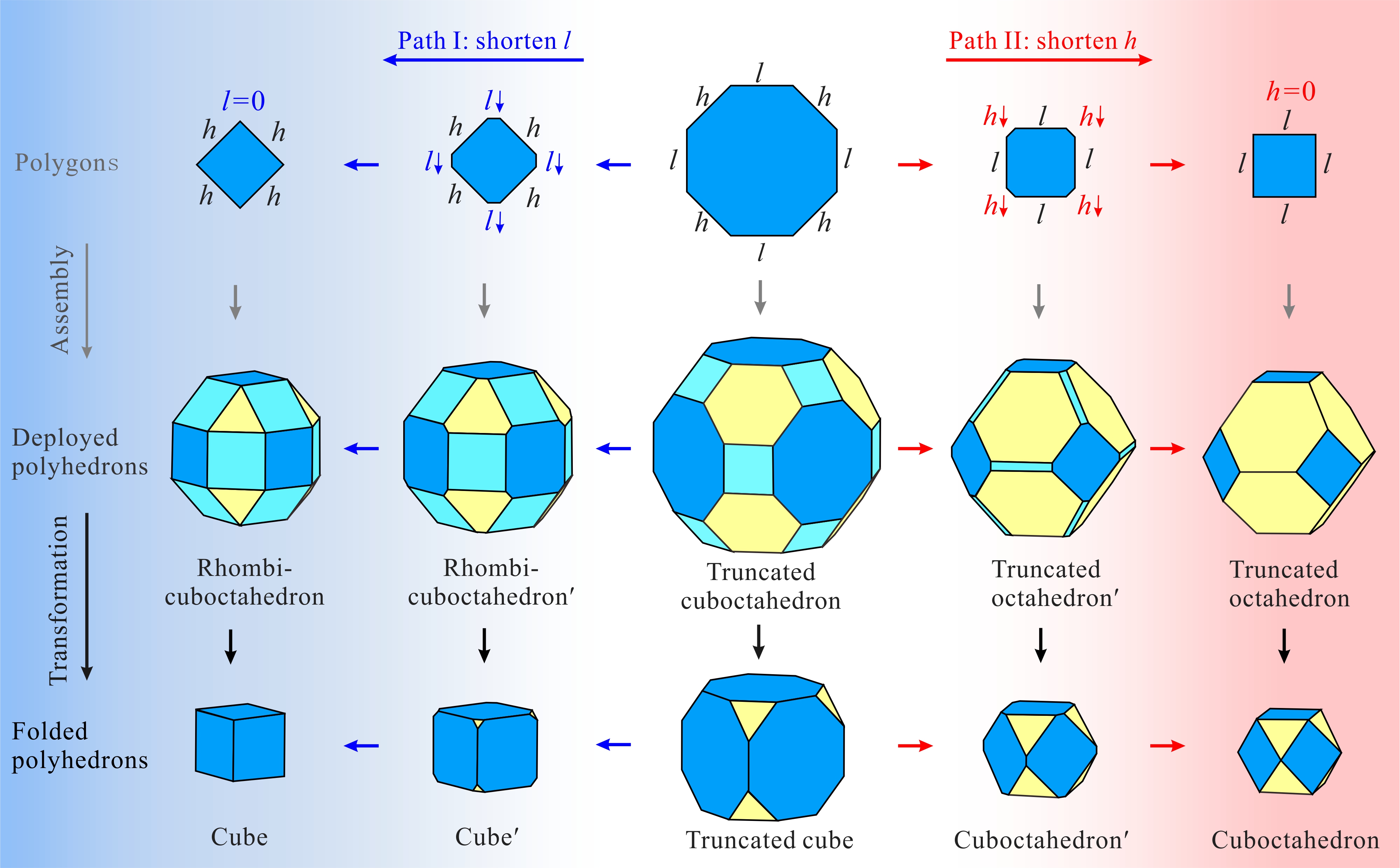
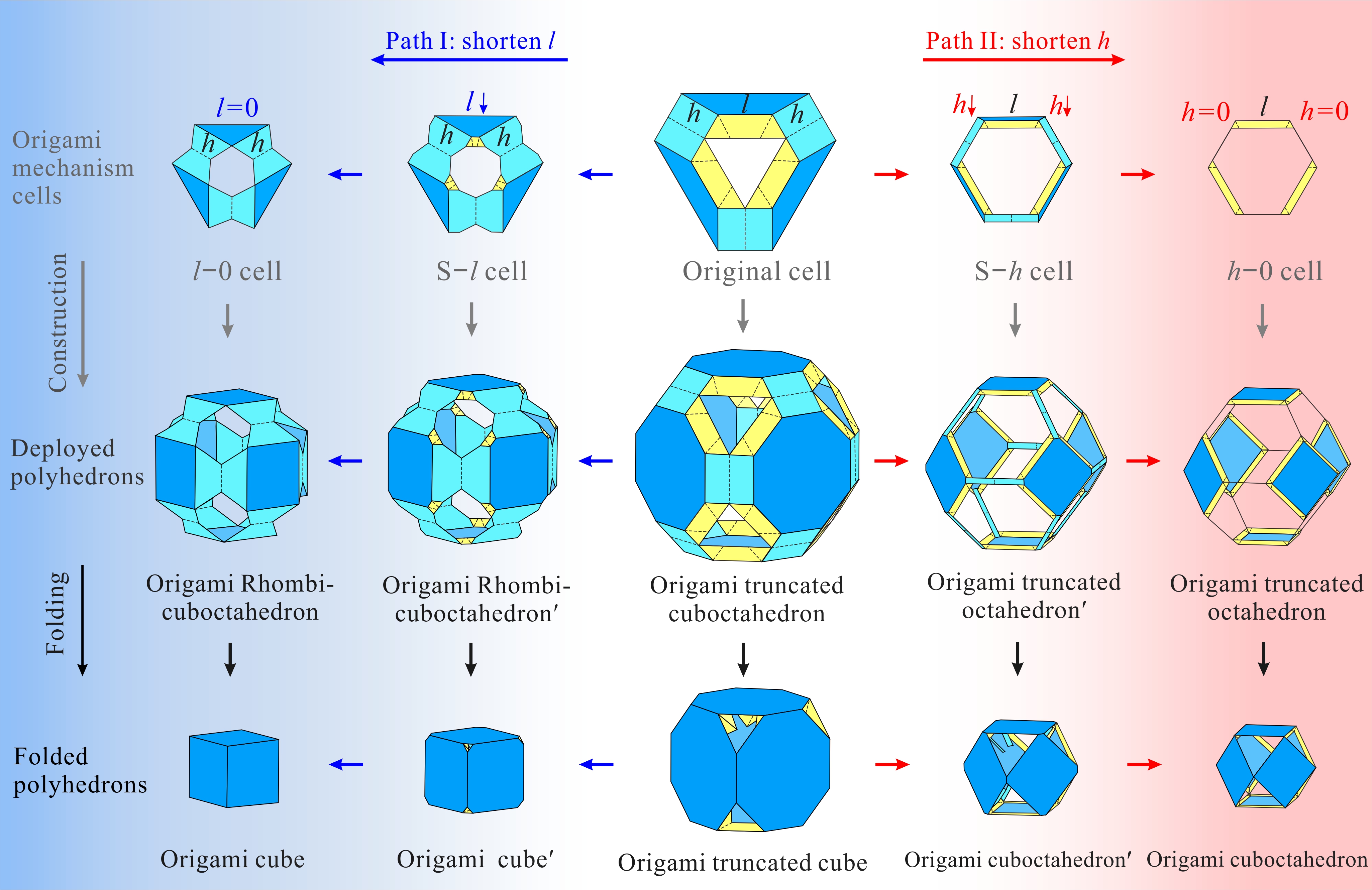
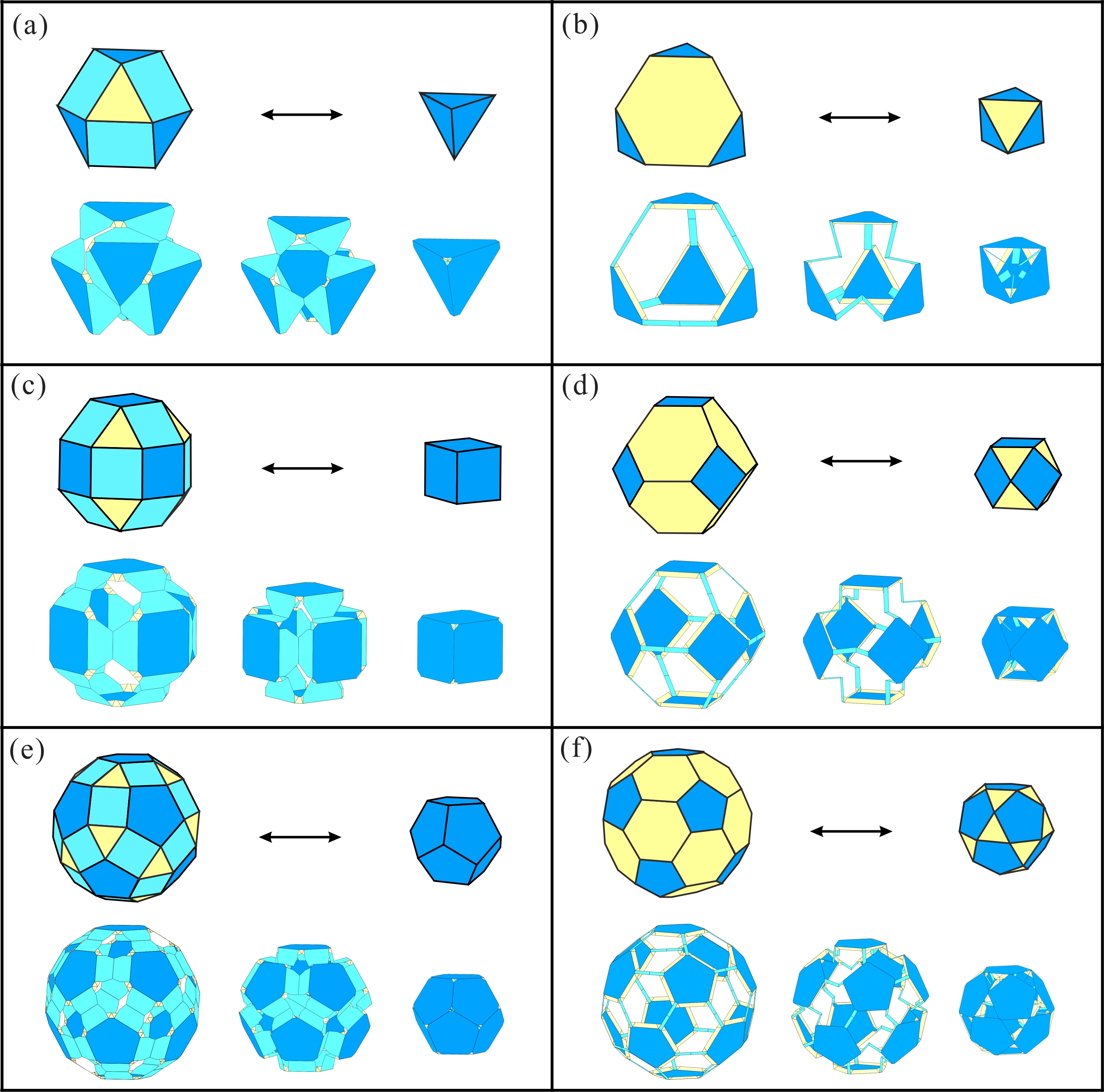
        Based on the original truncated cuboctahedron(Fig. 2b), Figure 3 presented dimensional shortening operations of polygons and polyhedrons as follows. The first row: the leftward path I to shorten side length l and the rightward path II to shorten side length h in an octagon; the second row: the corresponding polyhedral assemblies; the third row: the corresponding transformation results. Together with the dimensional shortening operations in Fig. 3 and the proposed construction method of the origami polyhedral mechanism, structural variations of origami polyhedrons are presented in Fig. 4. The first row: the leftward path I to shorten side length l and the path II to shorten side length h in an original mechanism cell. the second row: the folded configurations of the origami polyhedrons; the third row: the folded configurations. Here, the origami rhombicuboctahedron in path I and origami truncated octahedron in path II were obtained based on the origimal origami truncated cuboctahedron. Note that, due to mechanism topology isomorphism, the polyhedral mechanisms derived by dimensional shortening operations still perform one-DOF radial motion.

Fig. 3. Dimensional shortening operations.

Fig. 4. Variations of origami polyhedrons with shortening operations.

        Moreover, the proposed structural variations can be directly extended to the other two original origami polyhedrons in Fig. 2. In summary, a total of six transformations with structural variations relative to three original cases are list in Fig. 5, all of which can perform one-DOF synchronized radial motion.

Fig. 5. Six paired polyhedrons and their origami transformation solutions.

        This work was accepted by Mechanism and Machine Theory on 12 February, 2023 and published online on 18 February. The work in this paper potentially provides the new inspirations to create three-dimensional deployable structures and multifunctional metamaterials with enriched properties.

Gu Y, Chen Y*. Deployable origami polyhedrons with one-DOF radial motion. Mechanism and Machine Theory, 2023, 184, 105393.
(https://doi.org/10.1016/j.mechmachtheory.2023. 105293)