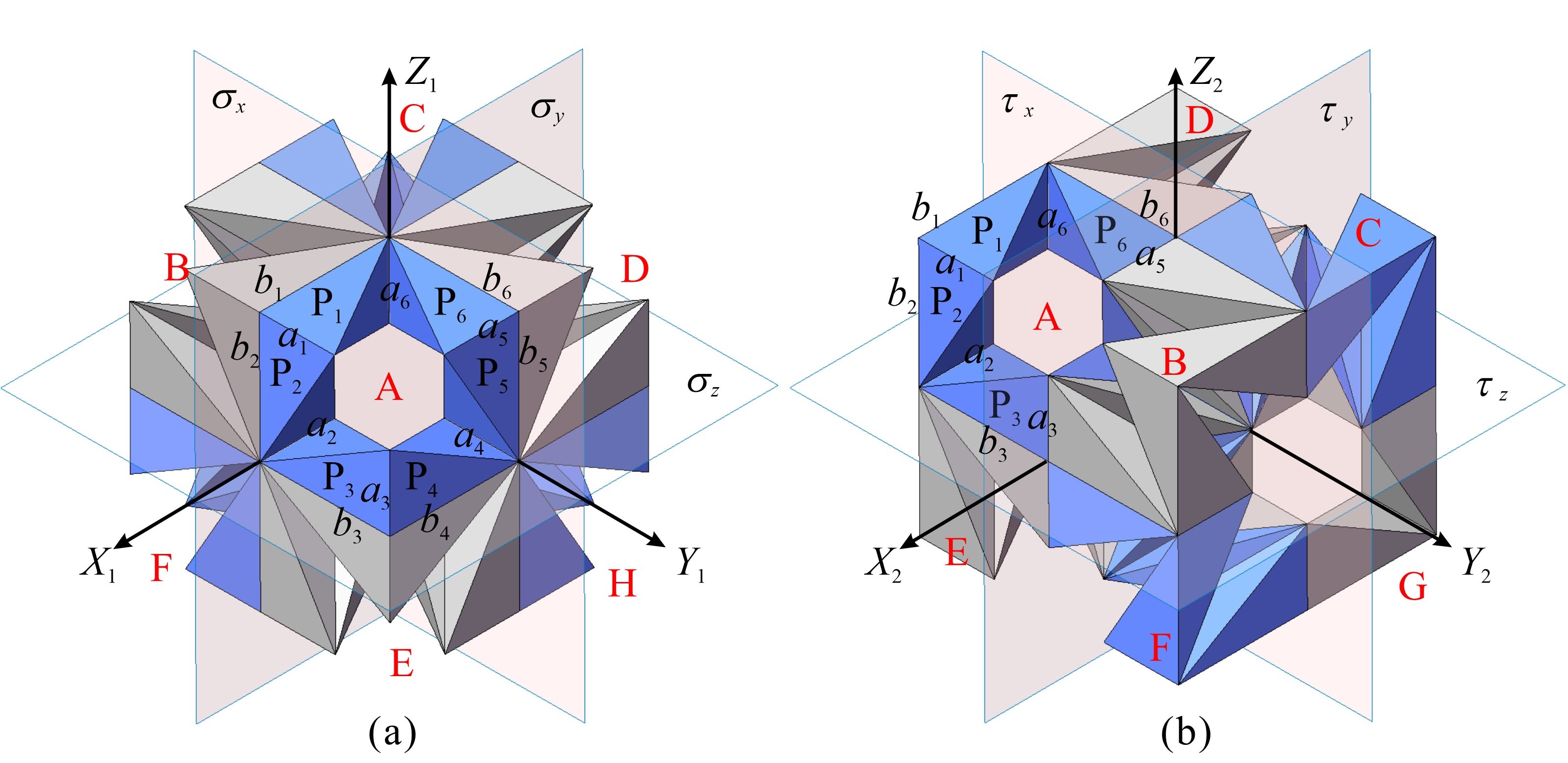
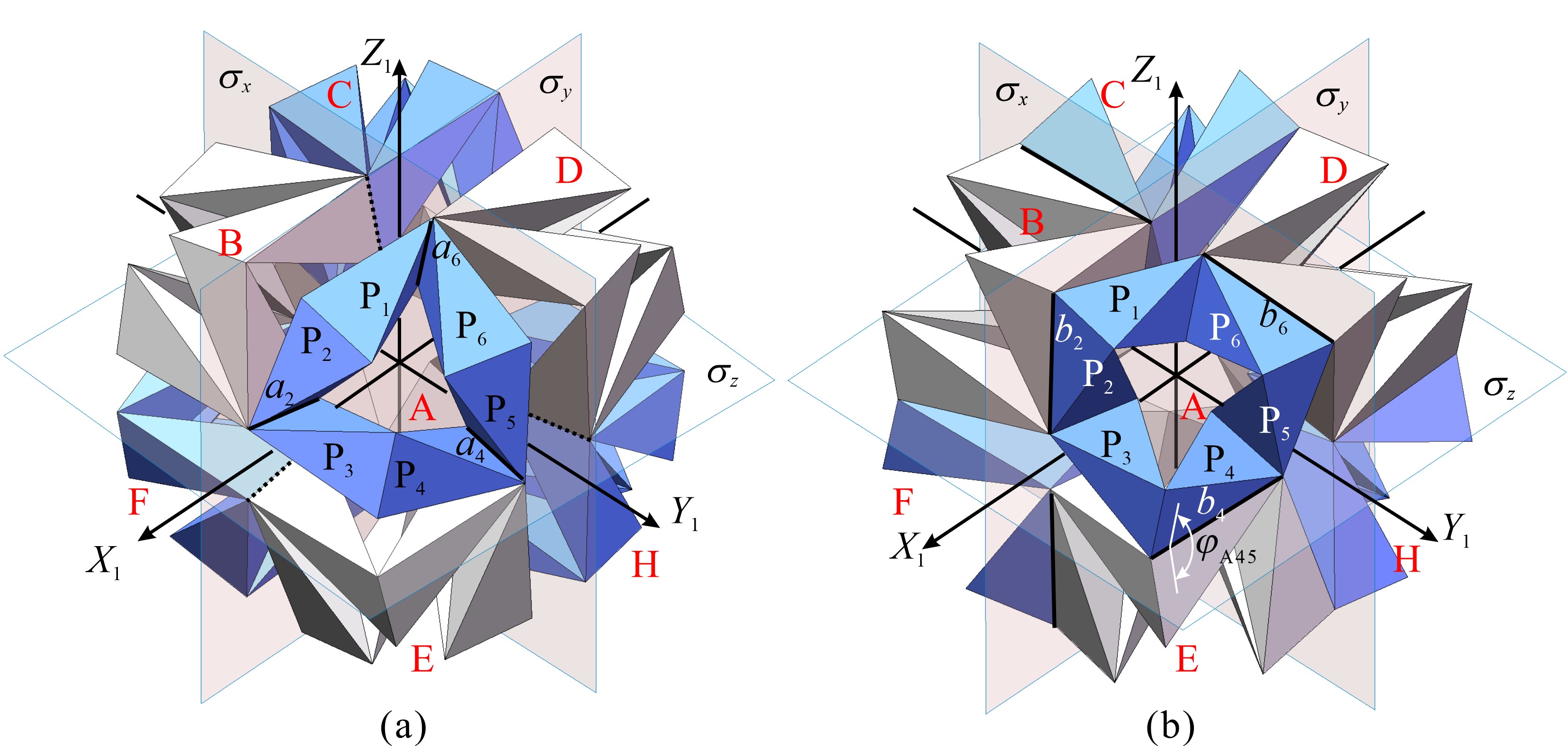
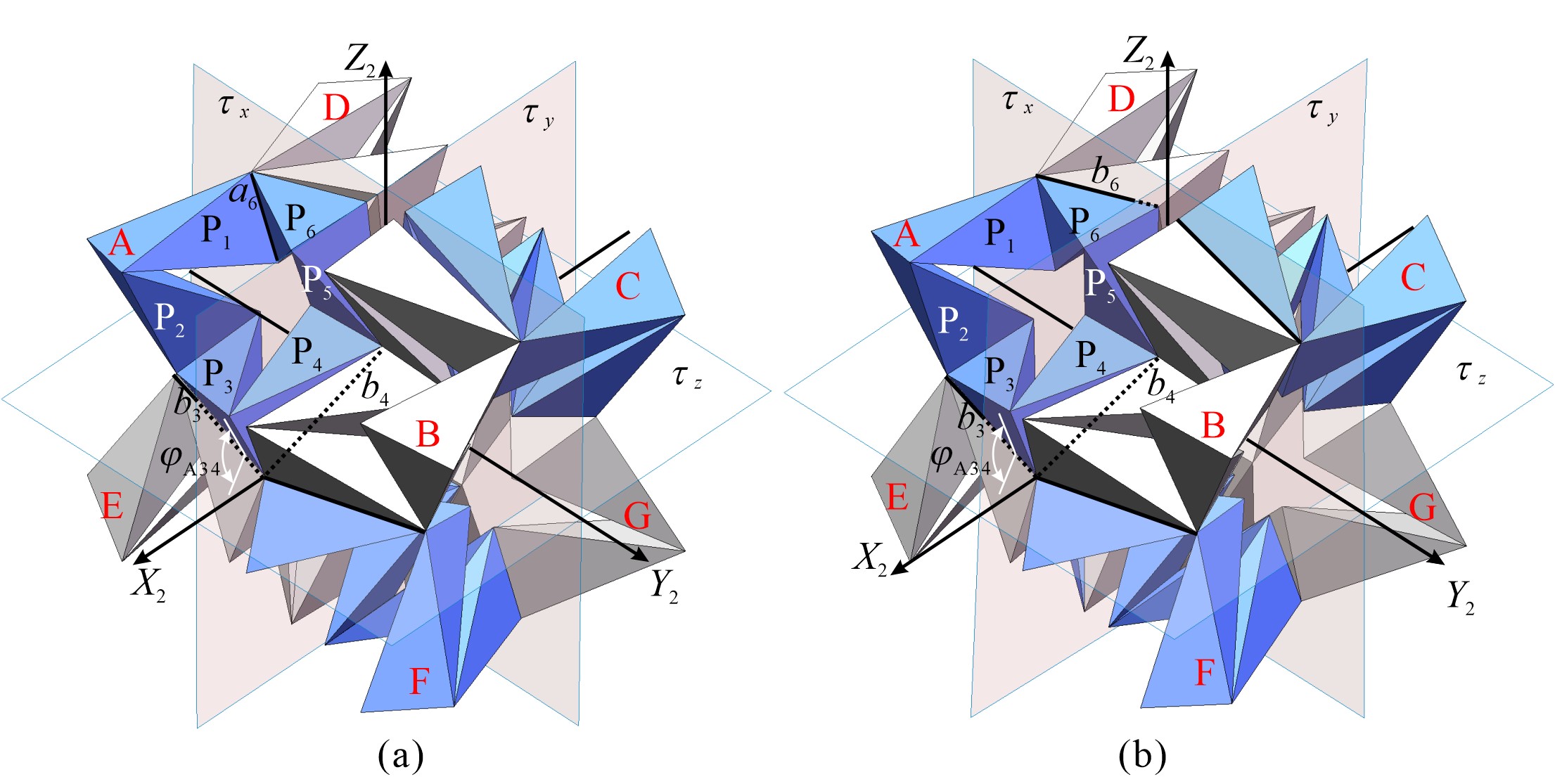
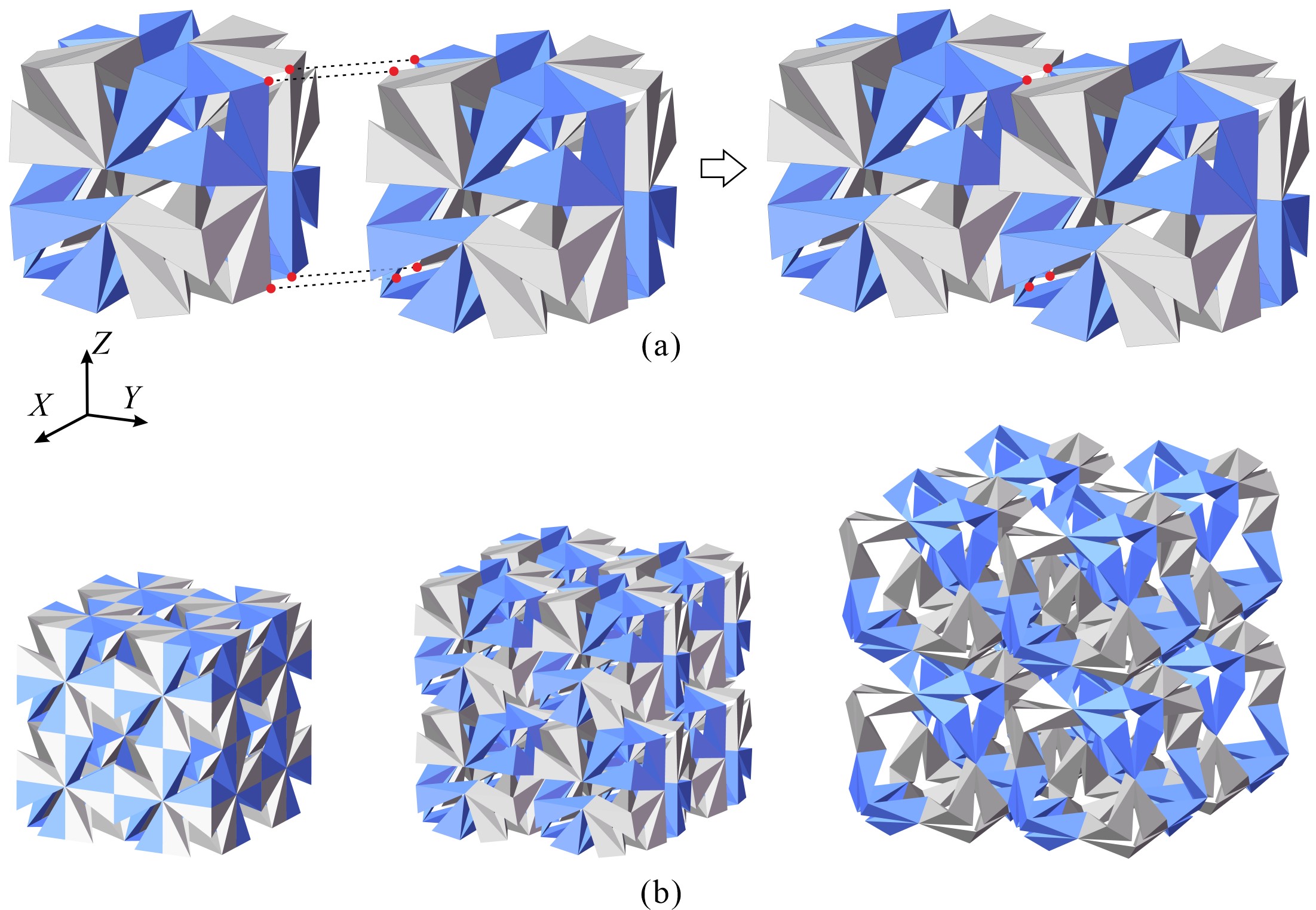
Spatial overconstrained mechanisms with single degree of freedom (DOF) are of superiorly foldable properties and have been widely used to design space deployable structures. To meet different design requirements, many spatial overconstrained mechanisms were regarded as units to be tessellated to deployable structures in two- or three-dimension (2D or 3D). However, most of the current research focuses on the 2D tessellations of units, and the number of mobile assemblies derived from 3D tessellations of linkages is limited.
        To solve this problem, Professor Chen Yan of the School of Mechanical Engineering of Tianjin University carry out 3D tessellation with kaleidocycles, a special type of threefold-symmetric Bricard linkages, as the basic unit, and obtained four mobile assemblies, and carried out kinematic analysis based on matrix method and numerical method.
        First, eight kaleidocycles linkages in a special configuration with rotation angles equal to 90 ° are symmetrically arranged in the space and obtain two arrangements A1 and A2 (Fig. 1). To form mobile assemblies, two adjacent units need to be connected by a common hinge. By discussing the motion characteristics of the assemblies according to the different hinge positions shared by adjacent units, two movable connection modes were obtained for the two symmetrical arrangements, and four mobile assemblies are constructed, as shown in Figs. 2 and 3.

Fig.1 Two spatial arrangements of eight kaleidocycles. (a) Spatial assembly A1 and (b) spatial assembly A2.

Fig.2 Two mobile assemblies of eight kaleidocycles under the spatial arrangements of A1. (a) Mobile assembly A1_1 and (b) mobile assembly A1_2.

Fig.3 Two mobile assemblies of eight kaleidocycles under the spatial arrangements of A2. (a) Mobile assembly A2_1 and (b) mobile assembly A2_2.

        Through the kinematic analysis of the above four mobile assemblies by numerical method, it is known that the mobile assembly A1_ 1 and A1_ 2 have two motion paths with different symmetric properties, cuboid symmetry and tetrahedral symmetry, see Fig. 3 and 4. The other two assemblies A2_1 and A2_2 are of single motion path keeping cuboid symmetry.

Fig.4 Analysis results of the mobile assembly A1_1

Fig.5 Analysis results of the mobile assembly A1_2

        The 3D tessellations of four mobile assemblies can be further realized by taking four mobile assemblies as basic units and connecting two adjacent units through S-joints, see Fig. 6. The 3D lattice of assemblies A1_1 has the potential to be used to design metamaterials with negative Poisson's ratio.

Fig.6 The 3D tessellation of assemblies A1_1

        This paper presents four types of 3D mobile assembly of eight kaleidocycles, special threefold-symmetric Bricard linkages, by sharing edges according to two symmetrical arrangements in space. Two of them are of bifurcation under kinematic analysis based on a numerical method combing the truss method and SVD method. The designing process facilitates the creation of new mobile assemblies under symmetry.

Zhang X, Zhou X, Li M*, Liu T, Xing J, Lv W, Yang F, Chen Y. Three-dimensional mobile assemblies based on threefold-symmetric Bricard linkages. Journal of Mechanisms and Robotics, 2023, 16(1): 014502.
(https://doi.org/10.1115/1.4062131)