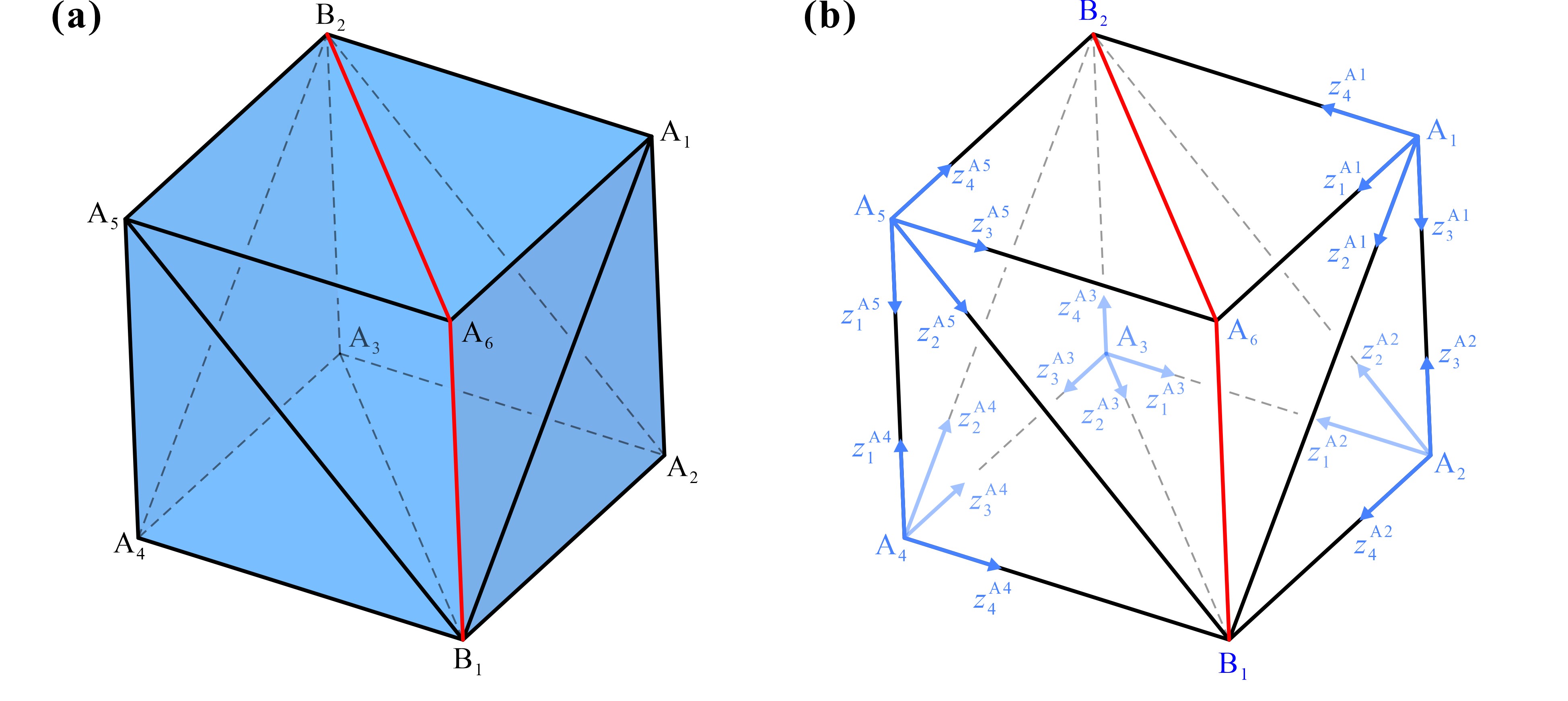
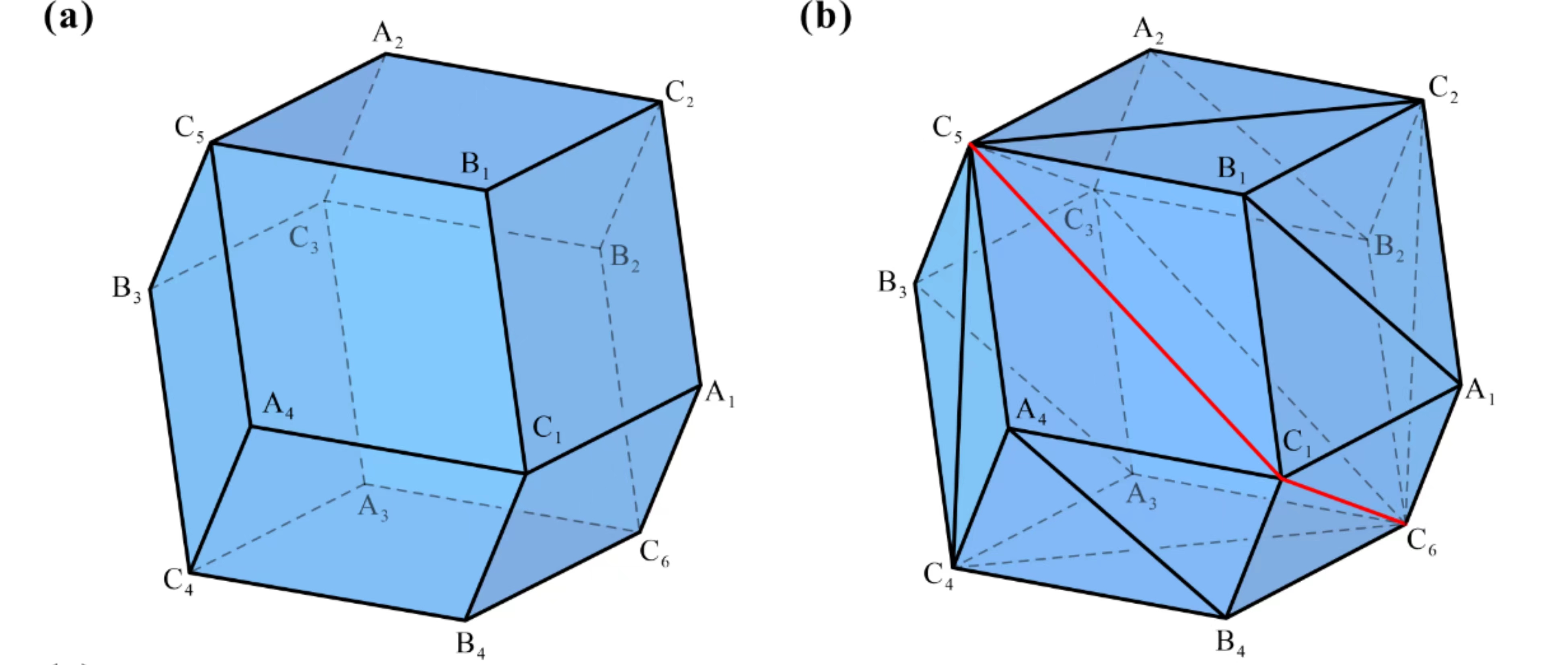
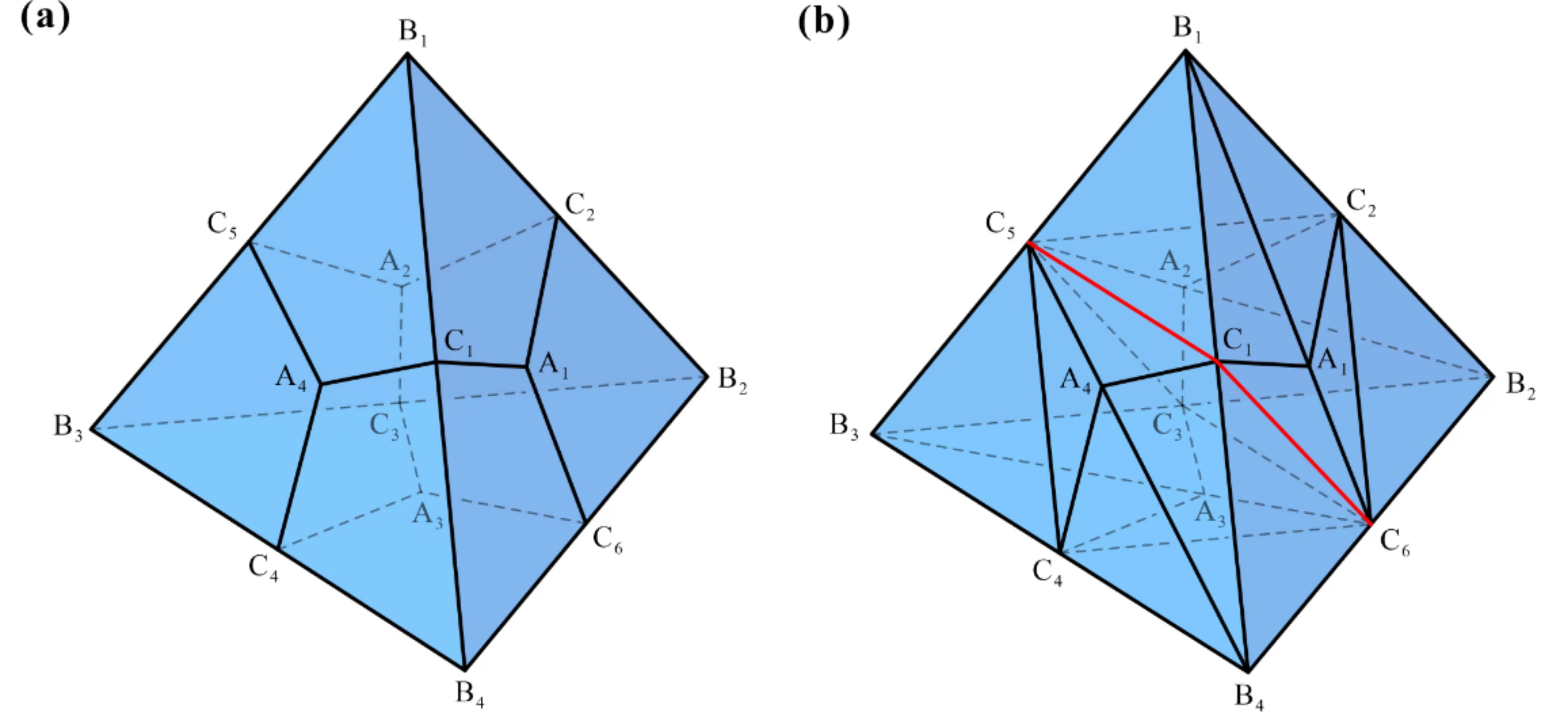
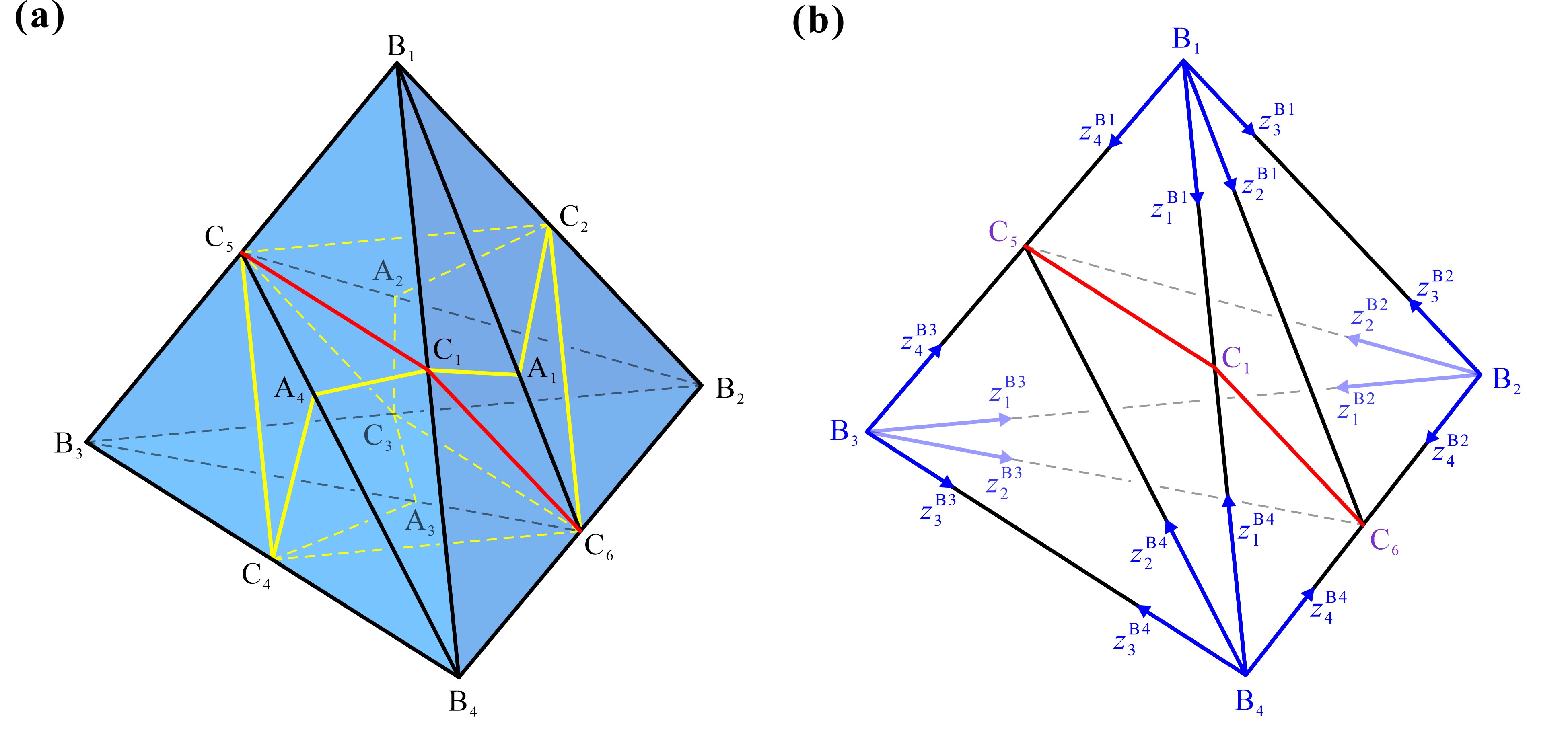
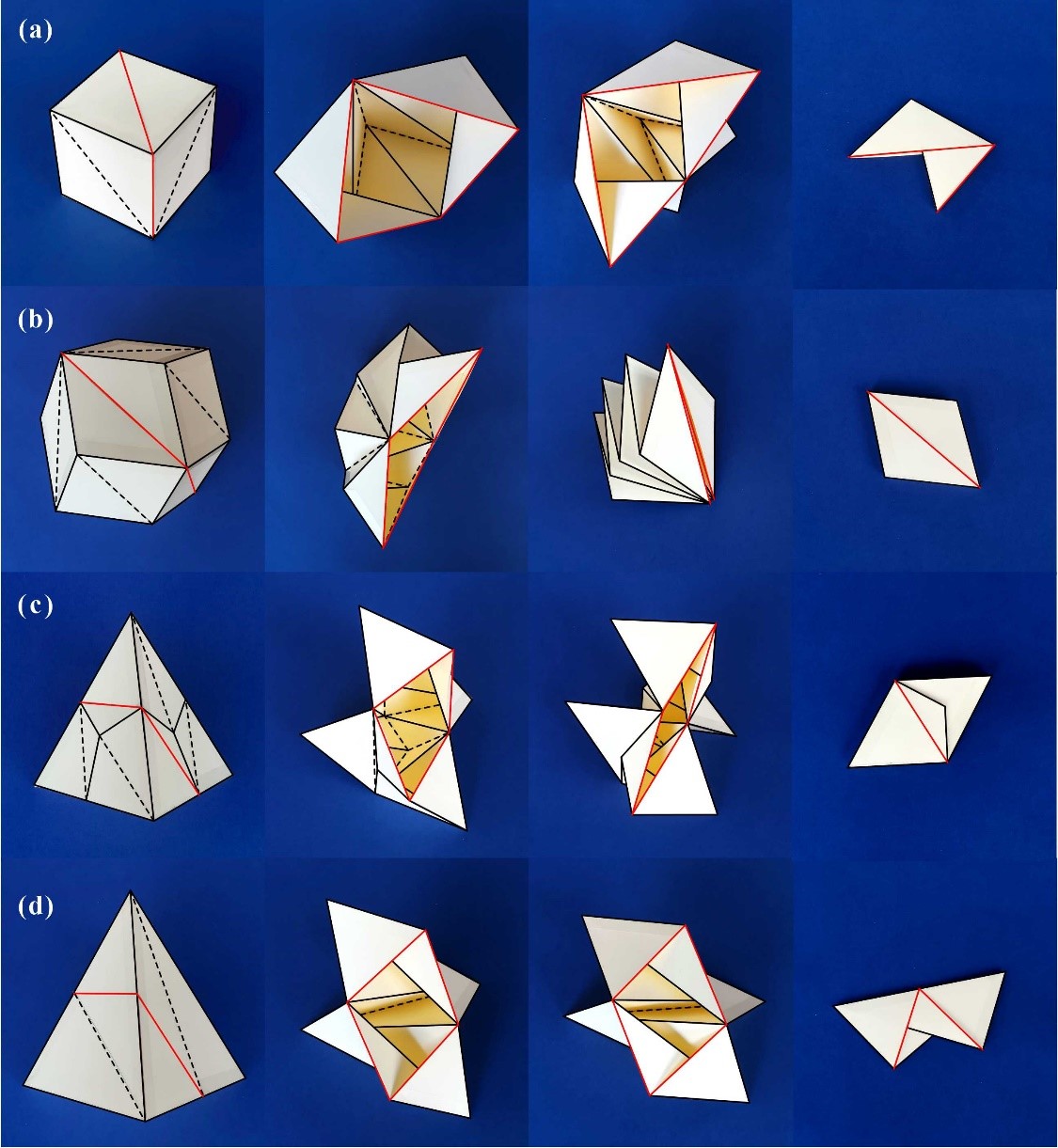
Rigid origami has great potential for aerospace applications, among which the one-degree-of-freedom (DOF) and flat-foldable origami polyhedrons are suitable to be used for space architecture and extraterrestrial habitats because they have excellent characteristics such as deploying to form enclosed structures and high deployed/folded ratios. However, there are currently very few types of one-DOF flat-foldable origami polyhedrons, which need to be studied urgently.
        To create more suitable deployable polyhedrons for applications, Prof. Yan Chen’s team at the School of Mechanical Engineering, Tianjin University, in collaboration with Senior Engineer Ming Li at Aerospace Systems Engineering Shanghai, designed several novel rigid and flat-foldable origami polyhedrons, all of which have one DOF and show good prospects for engineering applications.
        According to the bellows theorem, a closed polyhedron can’t be folded rigidly, so slits must be attached to the surface of polyhedrons. First, diagonal creases and slits were added to the surface of a cube, as shown in Fig. 1, where the creases are black and the slits are red, resulting in an origami cube with one-DOF rigid and flat-foldability.

Fig. 1. Origami cube. (a) a cube with creases (black) and slits (red); (b) coordinate systems.

        Similar to the cube, creases and slits are added to the surface of a rhombic dodecahedron, as shown in Fig. 2, resulting in a structure that is also rigid and flat-foldable with one DOF.

Fig. 2. Origami rhombic dodecahedron. (a) rhombic dodecahedron; (b) rhombic dodecahedron with creases (black) and slits (red).

        Subsequently, based on the similarity between rhombic dodecahedron and tetrahedron - they can be transformed to each other by the isohedral quadrilateral transform, the authors obtained a one-DOF rigid and flat-foldable origami tetrahedron by projecting the creases and slits of the rhombic dodecahedron onto the tetrahedron, as shown in Fig. 3.

Fig. 3. Origami tetrahedron. (a) tetrahedron derived from rhombic dodecahedron; (b) origami tetrahedron with creases (black) and slits (red).

        Finally, the author removed the unnecessary creases from the surface of the origami tetrahedron to create a simplified origami tetrahedron, as shown in Fig. 4, which also has one-DOF rigid and flat-foldability.

Fig. 4. Simplified origami tetrahedron. (a) the simplified origami tetrahedron with creases (black), slits (red), and creases to be removed (yellow); (b) coordinate systems.

        The physical models of the four origami polyhedrons and their folding sequences are shown in Fig. 5.

Fig. 5. The folding sequences of the physical models of the four origami polyhedrons. (a) origami cube; (b) origami rhombic dodecahedron; (c) origami tetrahedron; (d) simplified origami tetrahedron.

        This work was published in Acta Mechanica Solida Sinica. This work designed several novel flat-foldable origami polyhedrons that extend the family of deployable polyhedrons. Due to their one-DOF rigid and flat-foldability, these origami polyhedrons demonstrate great potential for aerospace applications.

Y. Zhang#, Y. Gu#, Y. Chen, M. Li*, X. Zhang*, One-DOF rigid and flat-foldable origami polyhedrons with slits, Acta Mech. Solida Sin. (2023).
(https://doi.org/10.1007/s10338-023-00404-0)