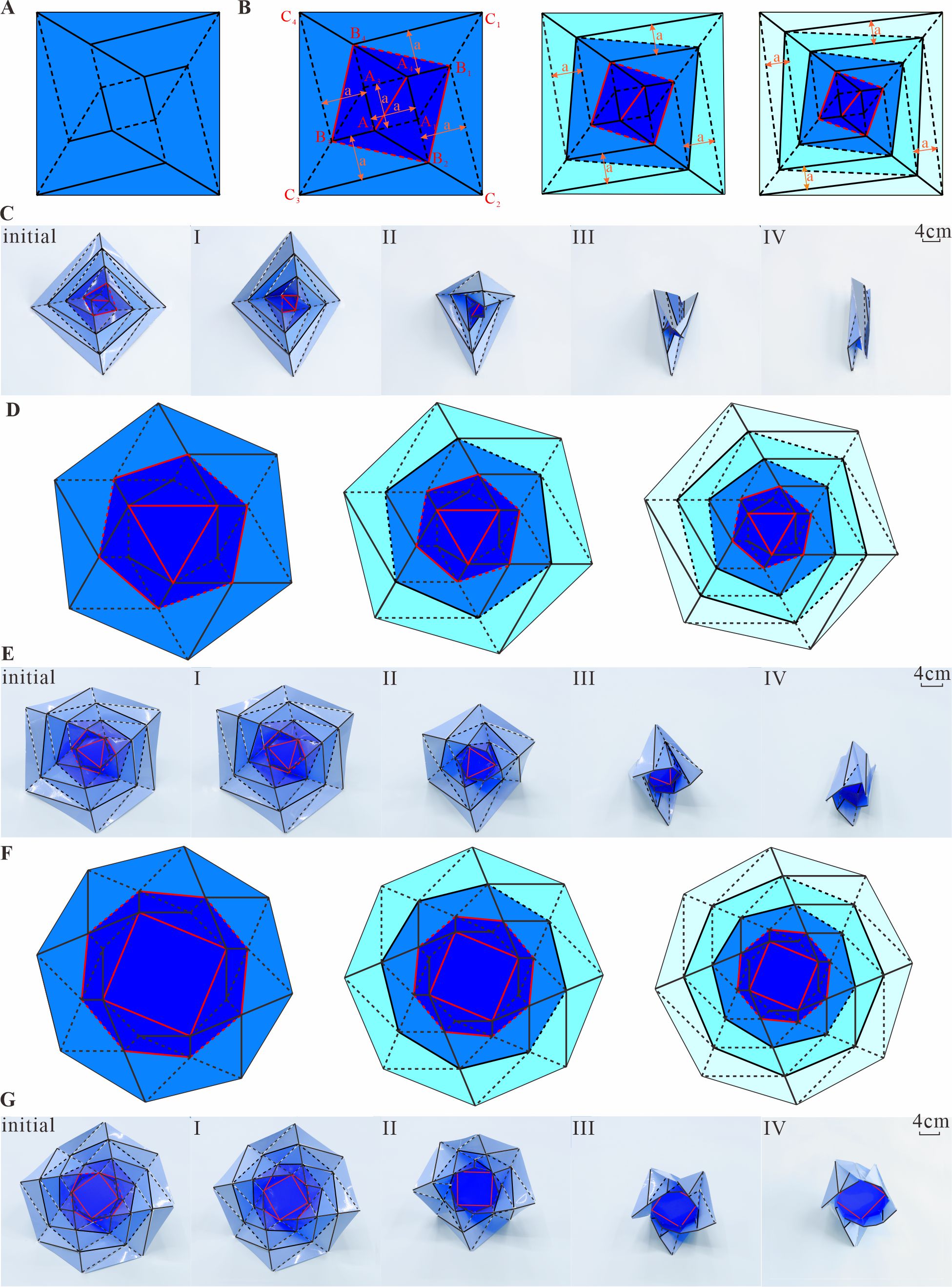
Recently, the team of Professor Yan Chen and Professor Jiayao Ma of Tianjin University proposed a series of extensible origami structures with multi-stability. Through kinematic analysis, the critical role of the delayed folding mechanics of the origami structure from the inside layer to outside was revealed, and the programmable multi-stable characteristics of the structure based on material and geometric parameters were explored through mechanical analysis. The relevant research was published online in the international journal Advanced Science on August 8, 2023 under the title of Multi-Stability of the Extensible Origami Structures. The co-corresponding authors of the paper are Prof. Yan Chen and Prof. Jiayao Ma from Tianjin University, and the co-first authors are Ph.D. students Kaili Xi and Sibo Chai from Tianjin University. The research was funded by the National Natural Science Foundation of China and the Tencent Foundation.

Background

        Bistable/multi-stable structures can rapidly switch among two or more stable states, thereby exhibiting diverse geometrical configurations and mechanical properties. These structures have found extensive applications in areas such as reconfigurable robotics, actuators, MEMS devices, mechanical logic, mechanical memory storage, mechanical signal propagation and other engineering fields. Non-rigid origami usually has two zero-energy states, the initial flattened state and the folded state. Take the original wrapping origami structure as an example, it can be folded from the flattened state to the state tightly wrapped around the central hub, and it is only geometrically coordinated in the flattened state and the tightly wrapped state. This unique feature makes them naturally suitable for the creation of bistable structures. However, achieving multi-stability often necessitates stacking multiple bistable units to form large 1D, 2D, or 3D structures or metamaterials. Few independent origami units exhibit multiple stable states, and the existing multi-stable origami units are often realized by motion bifurcation, which increases the difficulty of controlling at the bifurcation points, and the number of stable states is difficult to further increase through extending the origami patterns.

Highlight

        To address the above issue, the researchers tackled it by introducing additional creases to the original wrapping origami pattern depicted in Figure 1A. Then these creases were extended radially, resulting in the design of a range of extensible multi-stable origami structures with square, hexagonal, and octagonal hubs. The folding process of these origami structures is illustrated in Figure 1 and Movie 1. Each layer exhibiting rotational symmetry is successively wrapped around the central hub, starting from the innermost layer and progressing outward. The stability of the structure is achieved when each layer, excluding the central layer (highlighted within the red box), reaches a tightly wrapped state. Consequently, each outward extension of a layer introduces an additional stable state.

Figure 1. The crease patterns and physical specimens of the square, hexagonal, and octagonal extensible wrapping origami.

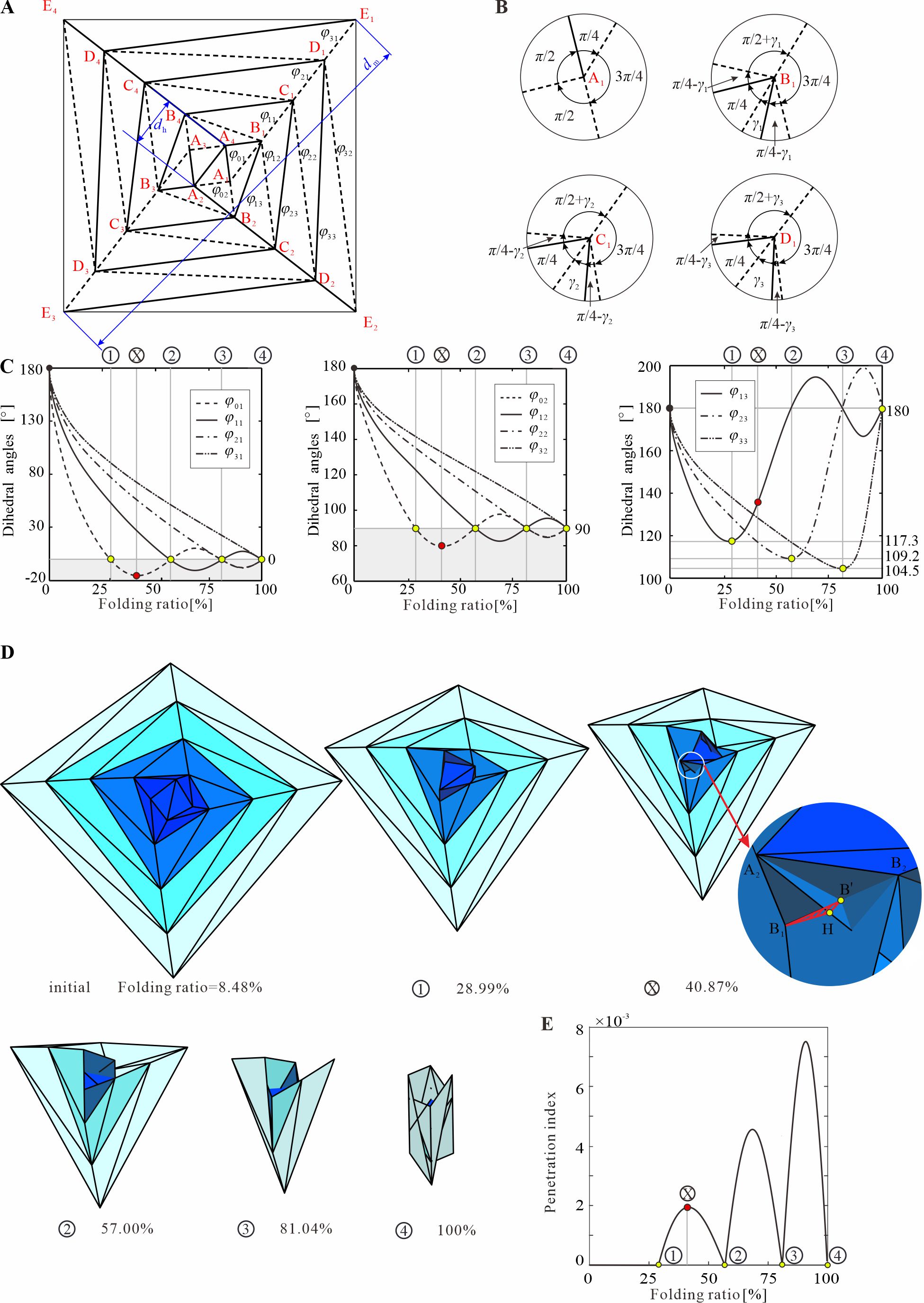
Movie 1

        To comprehend the folding mechanics and multi-stable behaviors of the extensible wrapping origami, the researchers investigated its kinematics using the Truss method firstly, focusing on the four-layer square wrapping origami as a representative example. As shown in the kinematic curves in Figure 2, the folding behavior between different layers of the structure are similar. Notably, there is a distinct folding delay observed among the dihedral angles at corresponding positions of the various layers. This unique sequential folding feature leads to a rigid origami range and three rigid origami states. These rigid origami states are separated by three non-rigid origami folding ranges, and the number of these states is determined by the number of layers extended.

Figure 2. The kinematic analysis of the four-layer square wrapping origami.

        After gaining insight into the sequential folding kinematics of the extensible wrapping origami patterns, here we investigate the deformation mechanics and multi-stable behavior through a combination of experiments and numerical simulations. Figure 3 and Movie 2 illustrate the results of uniaxial tensile loading on the origami structure. The force-displacement curve exhibits typical multi-stable characteristics, with the local peak force increasing layer by layer. By eliminating the influence of crease stiffness, we find that the stable states of the structure align well with the rigid origami states identified through kinematics, which proves that the unique sequential folding feature plays a critical role in generating multi-stability. Furthermore, we observe that as the stiffness ratio between the panel and the crease increases, the torsion of the crease becomes more pronounced, leading to higher local peak forces. Conversely, when the stiffness between the panel and the crease is low, the deformation mode of the structure changes, with the panel forming travelling hinges and resulting in a decrease in the local peak force.

Figure 3 Deformation and multi-stable behavior of the square wrapping structures.

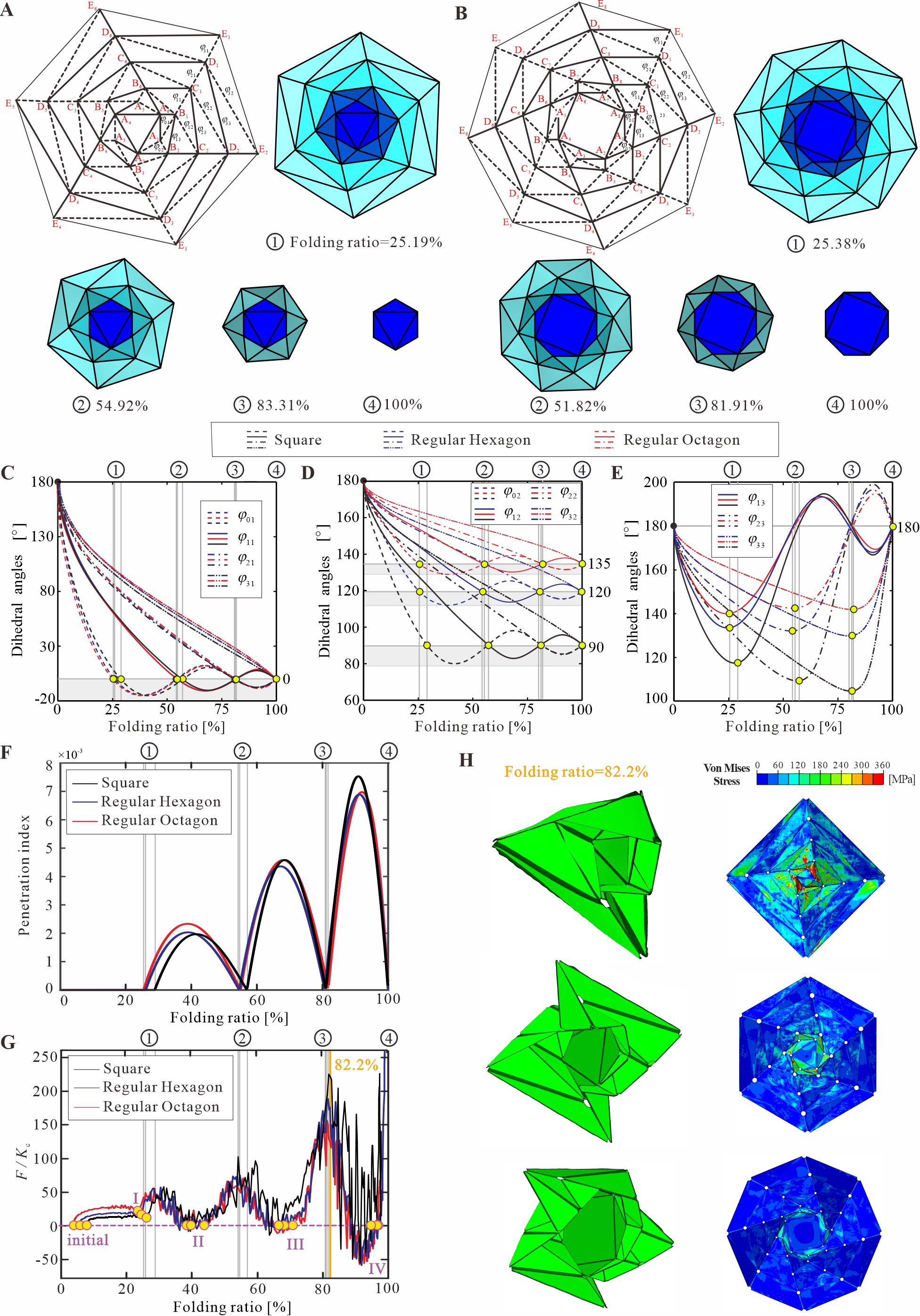
Movie 2

        The multi-stability is not a unique characteristic of the square wrapping structures. The researchers also examined the multi-stable behavior of four-layer hexagonal and octagonal extensible origami structures and compared them to the square one. The researchers also discovered that increasing the number of sides on the hub had minimal impact on the local peak force. However, it did have a significant effect on the maximum stress experienced by the entire structure. By increasing the number of sides, the maximum stress was reduced, resulting in a more uniform stress distribution, which can prevent or mitigate material failure during the folding process.

Figure 4. Multi-stable behavior of the extensible origami structures with different hub shapes.

Conclusion

        To summarize, this study designed a series of square, hexagonal, and octagonal extensible origami structures with multi-stability, and this structure can be tessellated to form larger ones with larger volume folding ratio. The structure shown in this paper only extends to four-layer wrapping origami structures, and it can be extended to more layers to obtain more stable states. In the future, researchers will employ the design principle in this work to develop multi-stable structures out of other non-rigid foldable origami patterns. This study offers a distinctive and effective design approach for generic multi-stable structures. Finally, efforts will be made to incorporate the multi-stable structures into advanced engineering applications such as soft robotics, mechanical computing, and multi-functional metamaterials.

Xi K#, Chai S#, Ma J*, Chen Y*. Multi-Stability of the Extensible Origami Structures. Advanced Science, 2023, 2303454.
(https://doi.org/10.1002/advs.202303454)