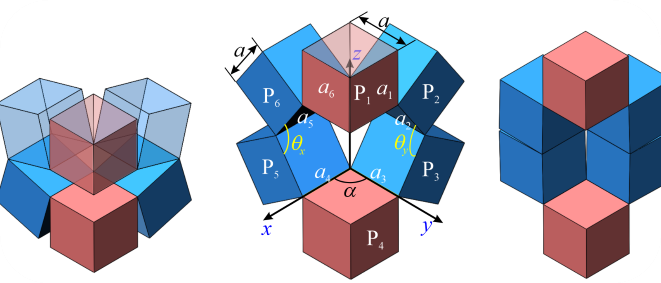
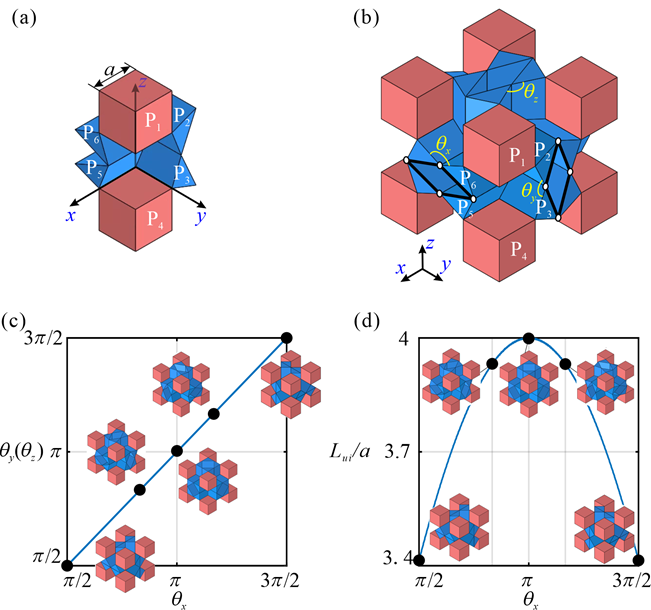
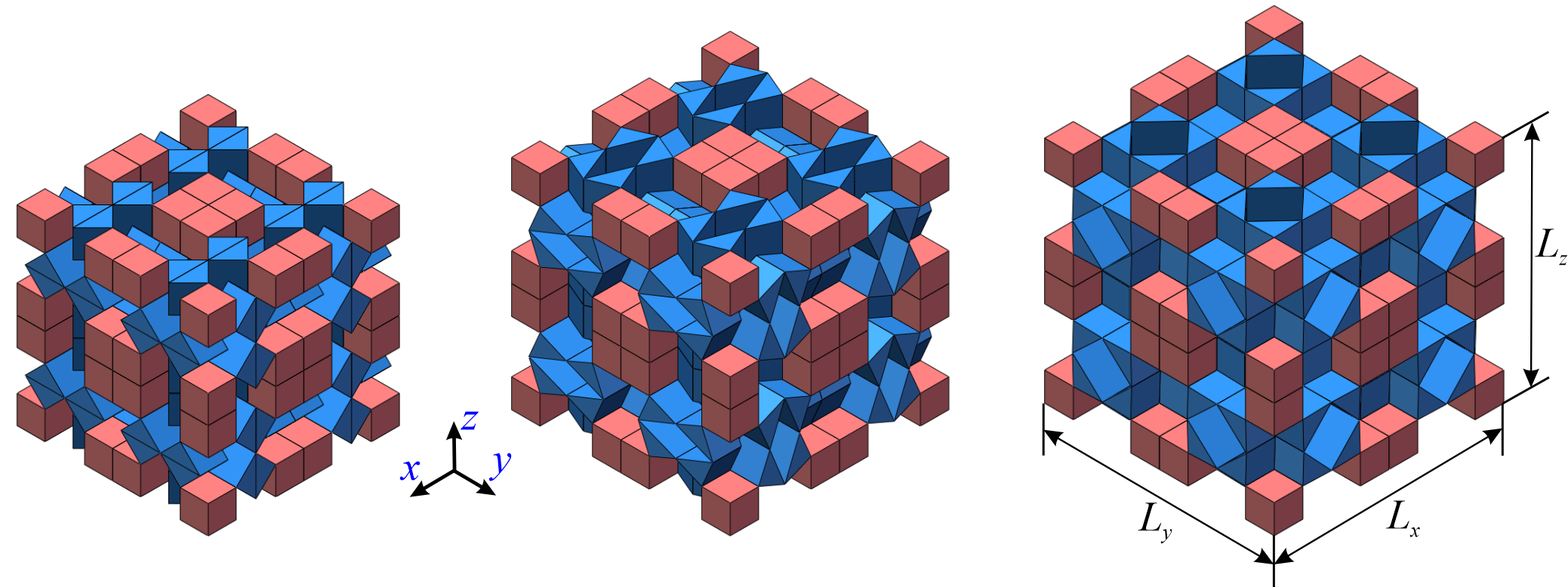
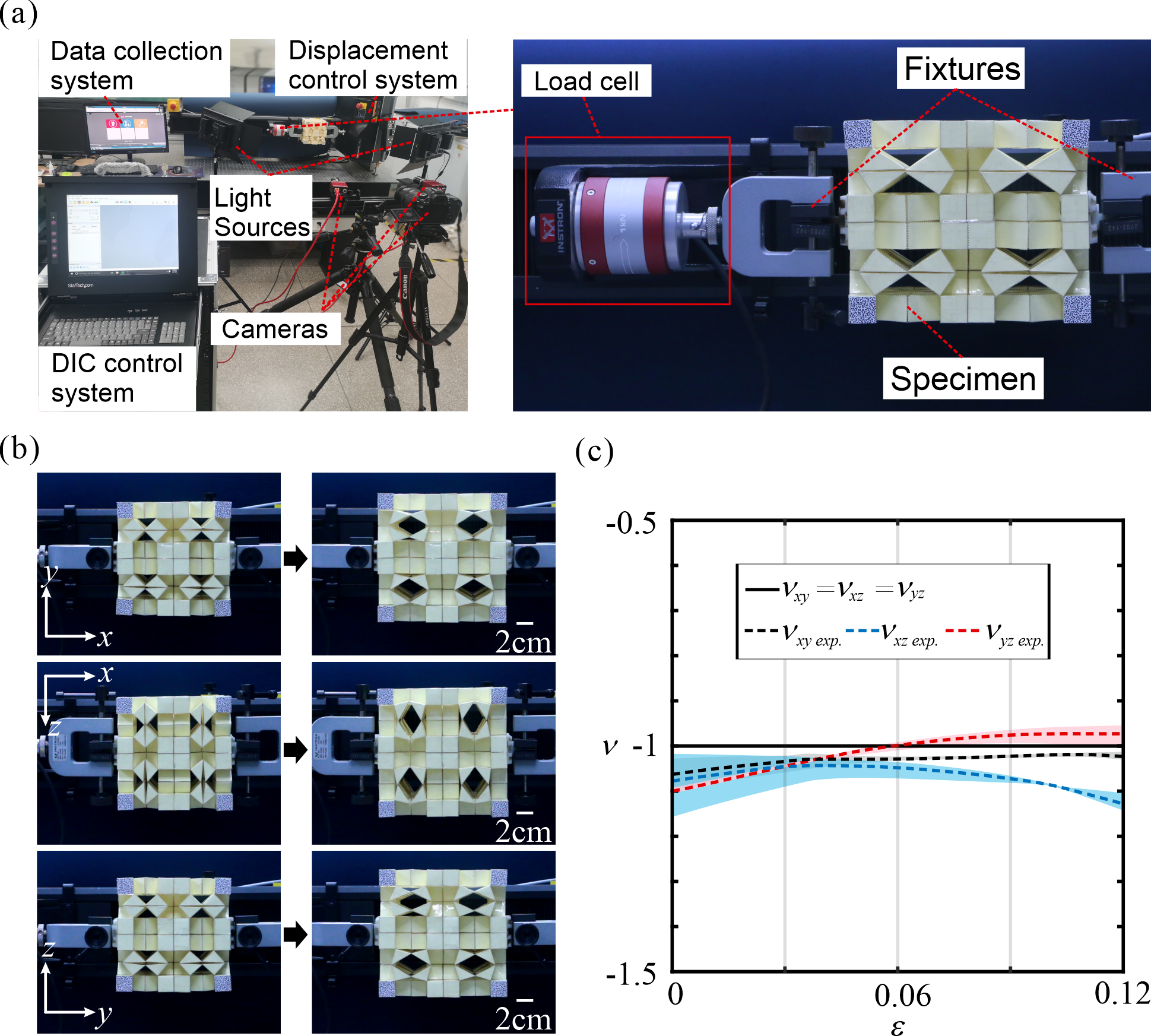
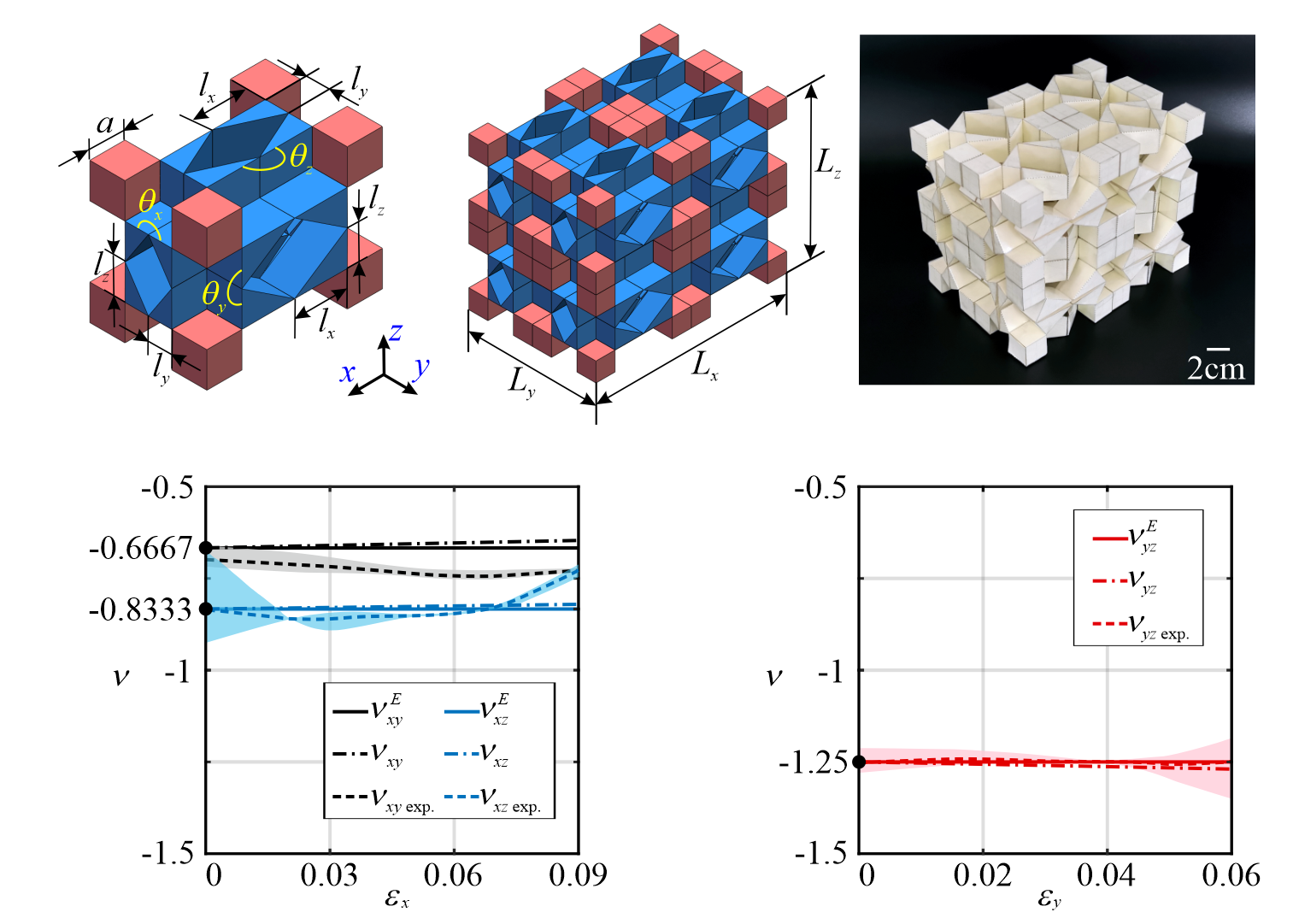
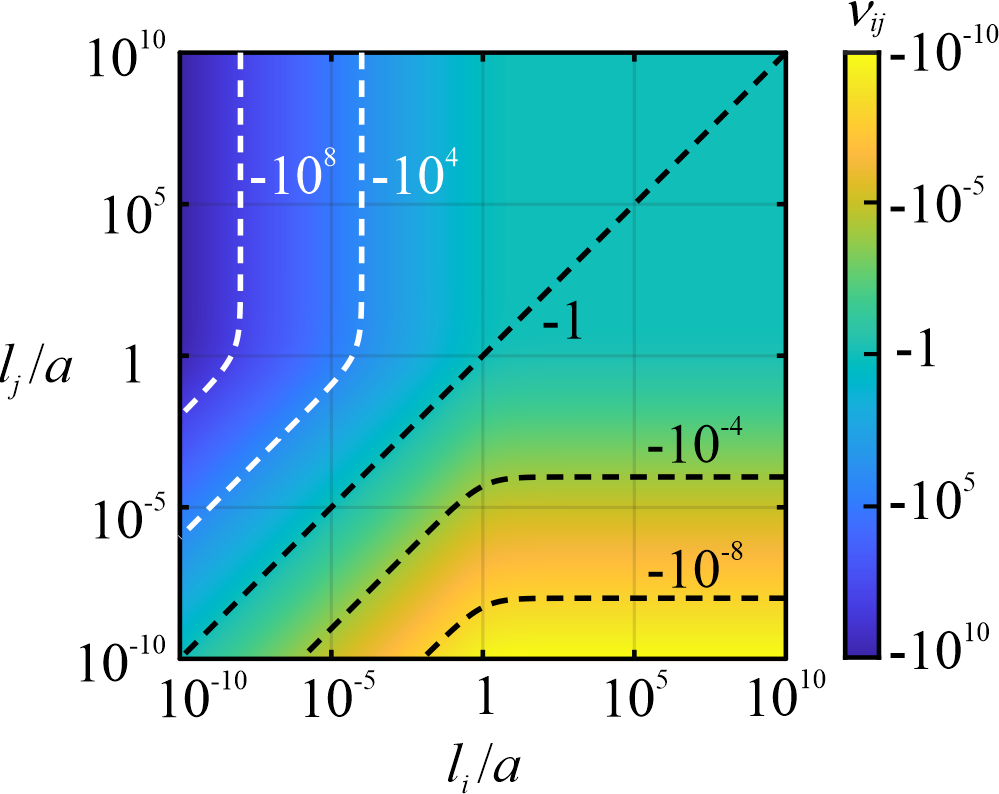
Metamaterials constructed from the periodic tessellation of units have extraordinary physical properties. The mechanical properties of most mechanical metamaterials are based on the large structural deformation of units, while the transmission and synchronization of these motion deformations among units are poor which leads to difficulty in designing and controlling the properties.
        To realize the programmable characteristics of constant negative Poisson's ratio, Prof. Yan Chen’s team at the School of Mechanical Engineering, Tianjin University, in collaboration with Prof. Zhong You’s team at the University of Oxford, designed a three-dimensional metamaterial with constant -1 Poisson’s ratios and a clearly defined deformation path based on the kinematics of classical Sarrus linkage and realized the programming of metamaterial with constant negative Poisson’s ratio by varying the geometrical parameters of the mechanism.
        First, the six cubes are connected sequentially by sharing edges to form a basic kinematic unit equivalent to Sarrus linkage, as shown in Fig. 1. By cutting half of the blue cubes to obtain triangular prisms, a basic kinematic element consisting of two red cubes and four blue triangular prisms is constructed, as shown in Fig. 2(a). Four elements are arranged in a mirror-symmetrical way, connecting through planar 4R linkages formed by the sharing edges of triangular prisms, and triangular prisms are added to the top and bottom surfaces. Thus, a kinematic unit with orthogonal characteristics and a single degree of freedom is created, as shown in Fig. 2(b).

Fig. 1. The basic kinematic element of the kinematic metamaterial with six cubes based on Sarrus linkage.

Fig. 2. The construction of an orthotropic kinematic metamaterial. (a) the modified element by cutting half of the blue cubes; (b) an orthotropic kinematic unit of four elements with triangular prisms on the top and bottom surfaces; (c) the deformation path of the orthotropic unit and the typical states, and (d) the dimensions of the unit during the movement.

        Eight kinematic units can be tessellated in space by sharing facets to construct a metamaterial of 2×2×2 units, as shown in Fig. 3. Through theoretical calculation and experimental verification, as shown in Fig. 4, it is found that the metamaterial has a constant -1 Poisson’s ratio characteristic.

Fig. 3. A 2×2×2 unit metamaterial constructed by tessellating the unit in three orthogonal directions.

Fig. 4. Experimental process and Poisson’s ratio results of the metamaterial.

        We then established the relationship between the geometric dimensions (lx, ly, lz) of the triangular prism in the kinematic units and the Poisson’s ratio of the metamaterial. By varying the geometric dimension, the theoretical Poisson’s ratio and engineering Poisson’s ratio of the metamaterial structure are calculated respectively, and the comparison shows that they are approximately constant and equal. A metamaterial with dimensions lx = 3a/2, ly = 2a/3, lz = a was designed and the experimental results show that the metamaterial has different constant negative engineering Poisson’s ratios which are approximately equal to theoretical Poisson's ratio and experimental results, as shown in Fig. 5.

Fig. 5. The metamaterial with anisotropic constant negative Poisson’s ratios.

        Further, in the variation range (0,+∞) of the geometric dimensions of the triangular prism, the instantaneous Poisson’s ratio of the metamaterial can be programmed in the range (-∞,0).

Fig. 6. The contour of Poisson’s ratios vs. li/a and lj/a (i, j = x, y, z and i ≠ j).

        This work was published in Materials & Design. This work proposed a new approach for constructing programmable metamaterials based on the kinematics of linkages, which is conducive to the design of novel programmable metamaterials.

Yang Y#, Zhang X#, Maiolino P, Chen Y*, You Z*. Linkage-based three-dimensional kinematic metamaterials with programmable constant Poisson’s ratio. Materials & Design, 2023, 233, 112249.
(https://doi.org/10.1016/j.matdes.2023.112249)