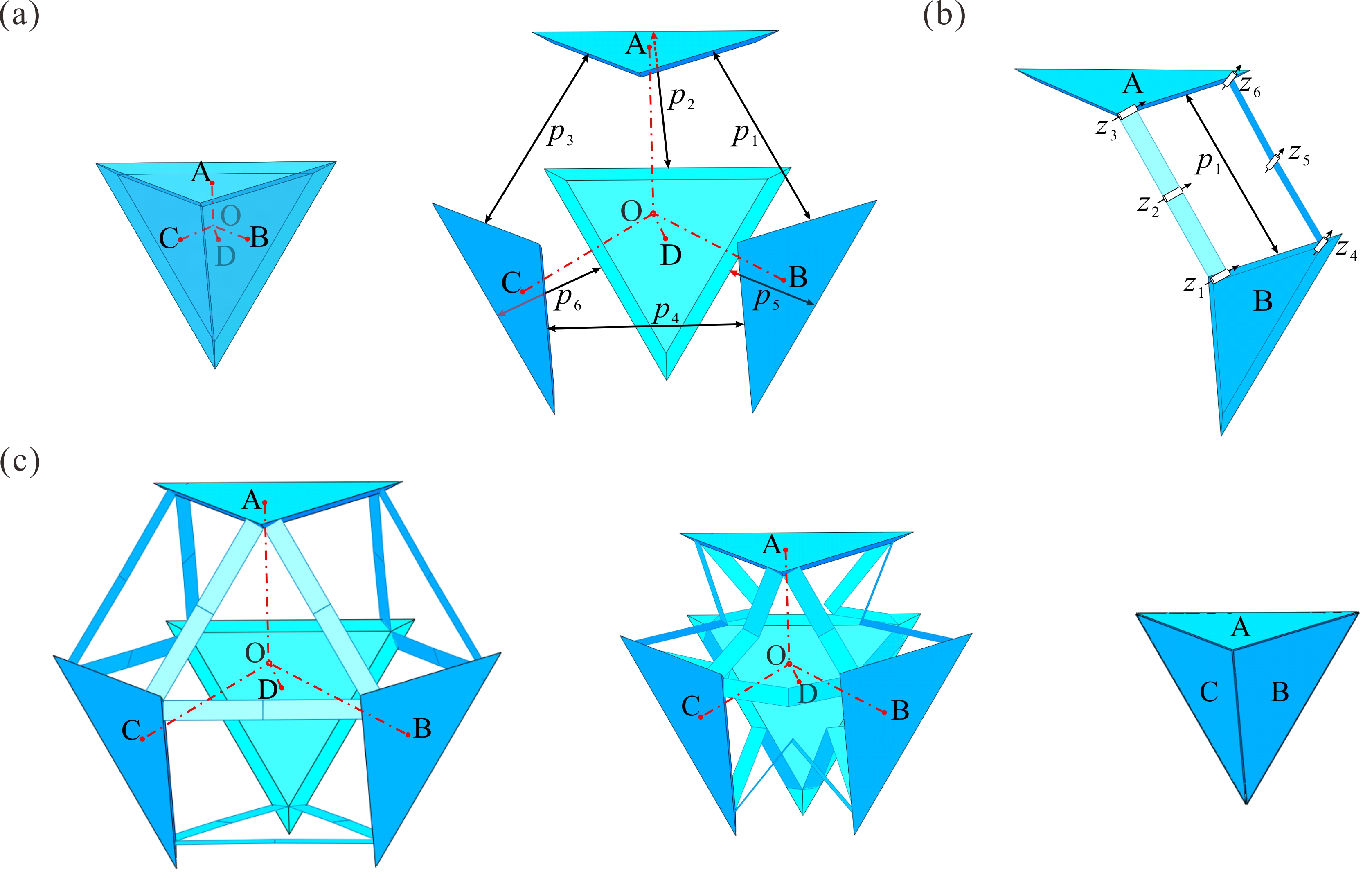
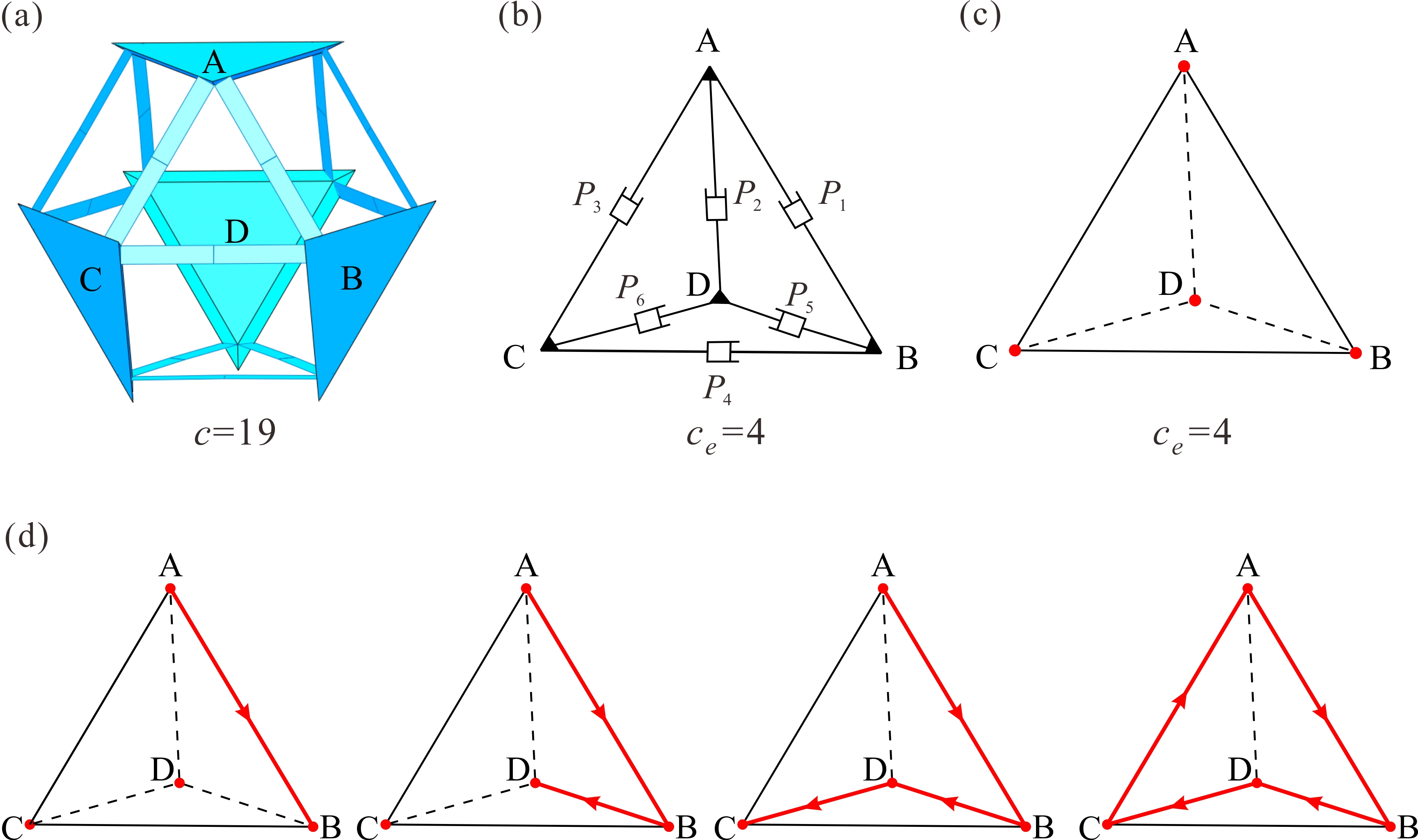
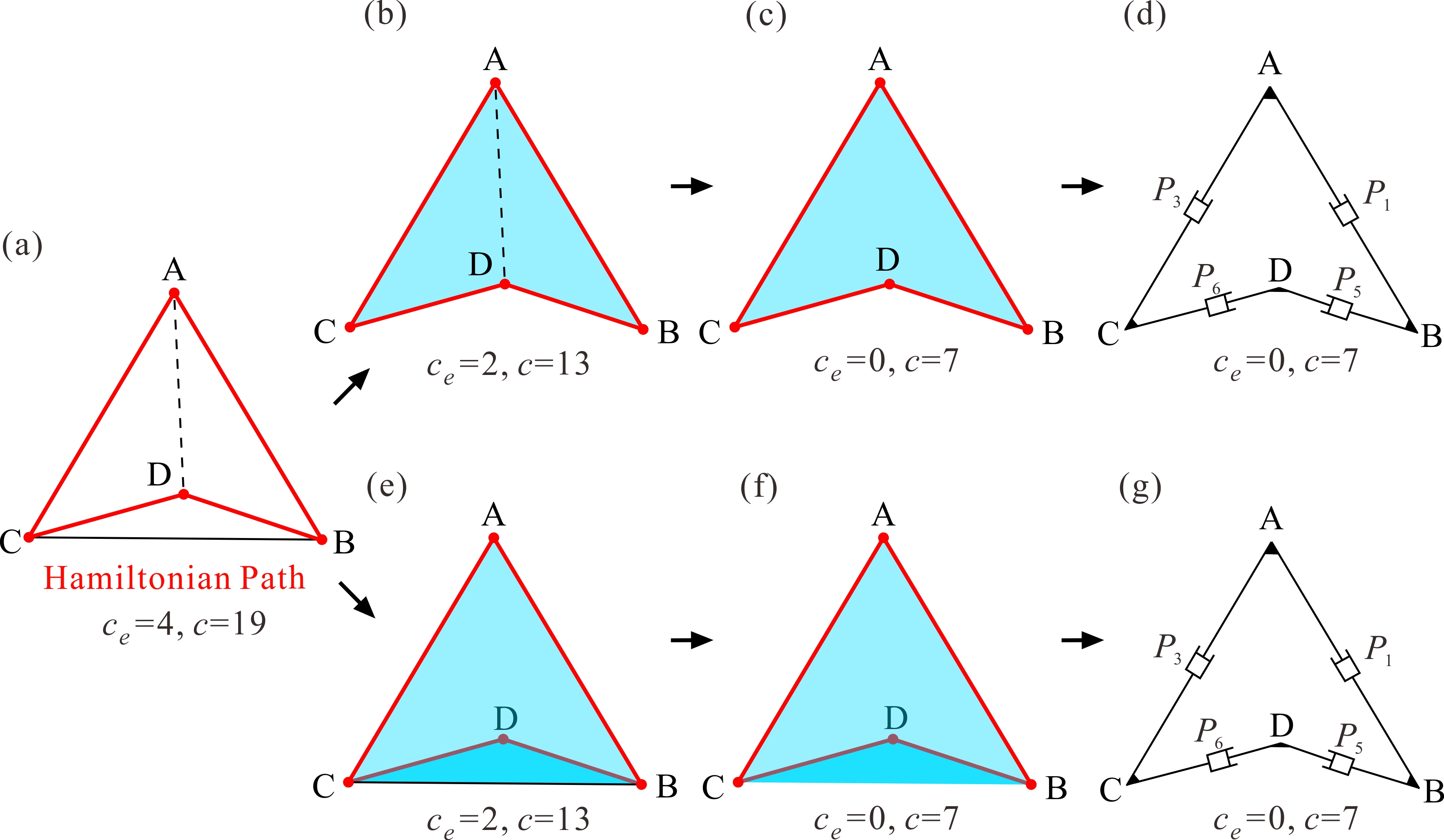
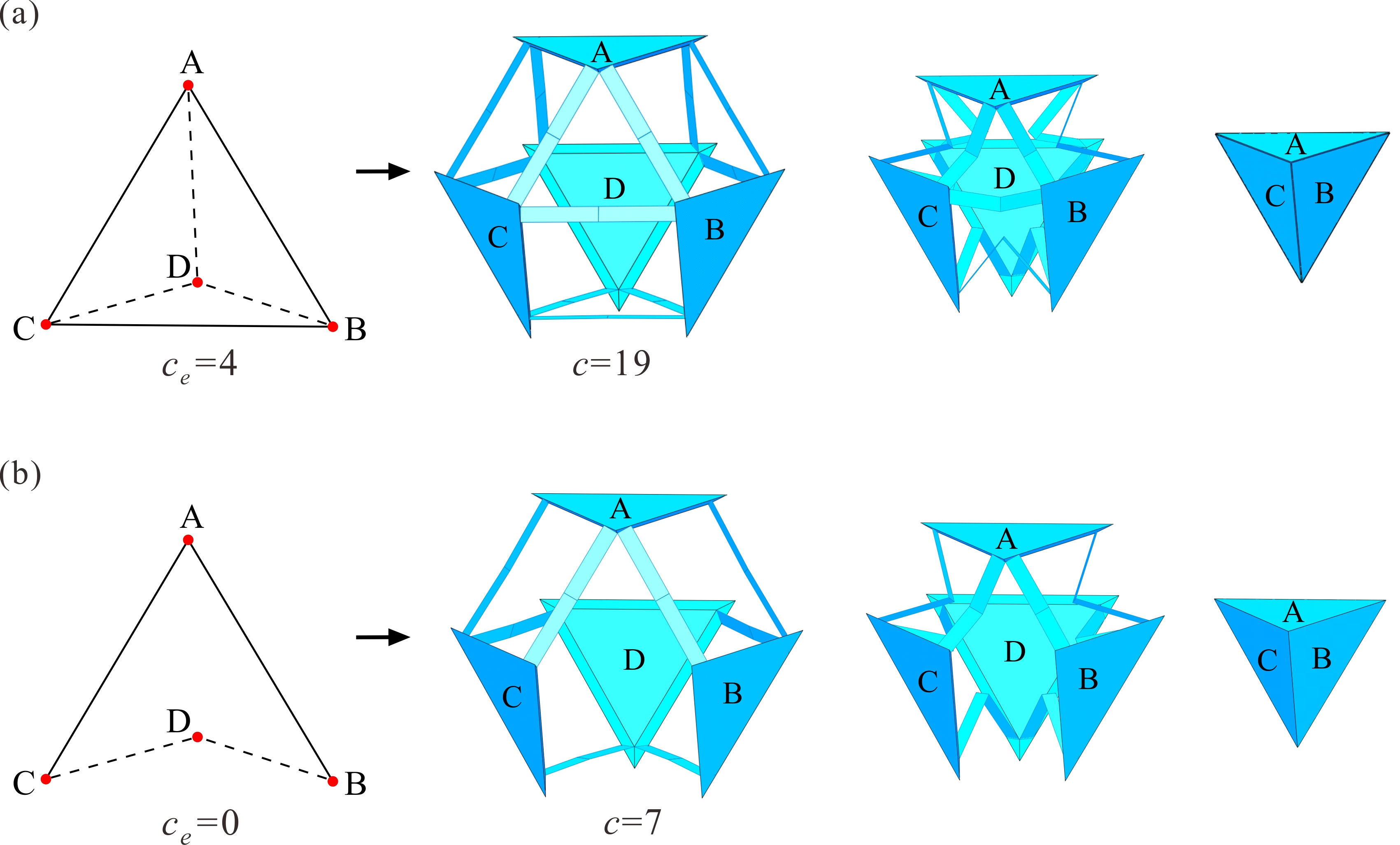
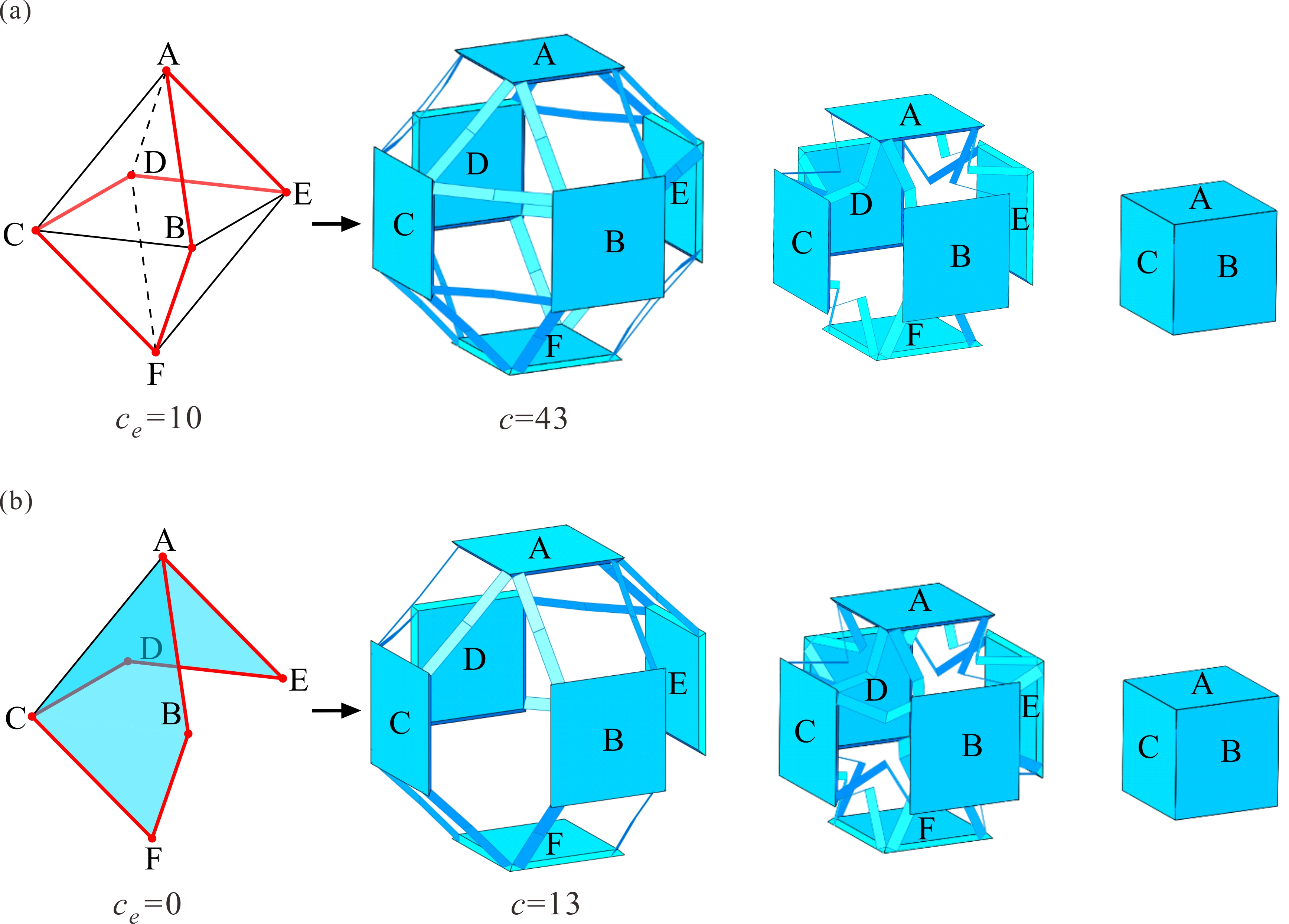
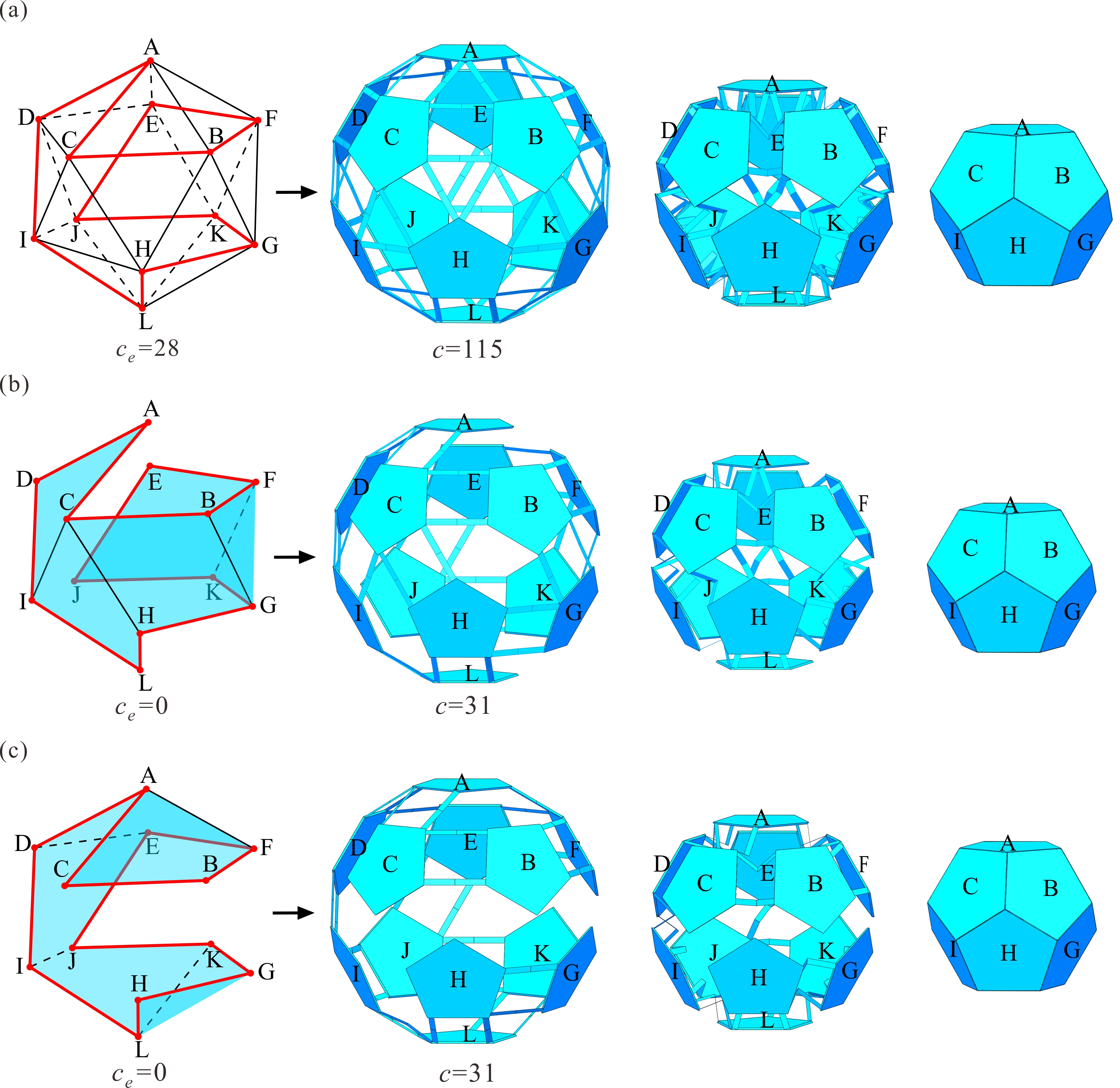
The design of deployable polyhedral mechanisms (DPMs) combines the ingenious inspirations of mechanism kinematics and solid geometry, yet it remains challenging to realise one-degree-of-freedom (DOF) transformations between two regular polyhedrons with a kinematic strategy. Moreover, most of these transformations involve spatial, multiloop, and overconstrained mechanisms that have limited their application potential. Thus, overconstraint reduction based on kinematic equivalence has become a problem that needs to be solved. The authors designed a family of DPMs with 1-DOF synchronized radial motion based on Sarrus linkages, and proposed the overconstraint reduction strategy for multiloop overconstrained mechanisms by introducing Hamiltonian paths, in which the degrees of overconstraint in each Sarrus-based DPM are greatly reduced without affecting the original kinematics.
        First, by carrying out the expansion operation, four platforms of a tetrahedron (T_d symmetry) are separated synchronously and moved radially and each pair of adjacent triangular prismoid platforms undergoes a straight-line motion, as shown in Fig. 1a. To enable this motion, the Sarrus linkage is adopted because it can generate the exact straight-line motion between two platforms, see Fig. 2b. Furthermore, we can take a similar implantation and integrate six Sarrus linkages into each pair of two adjacent platforms along straight-line paths. Thus, a novel deployable tetrahedral mechanism is obtained, as shown in Fig. 1c, which consequently leads to a transformation from a rhombitetratetrahedron (the deployed configuration) to a tetrahedron (the folded configuration).

Fig. 1. Construction of the one-DOF deployable tetrahedral mechanism

        Thus, the original degree of overconstraints c in this mechanism can be derived as c=19. The proposed tetrahedral mechanism is illustrated in Fig. 2a, as well as its equivalent mechanism with six prismatic joints (Fig. 2b) with c_e=4 and the corresponding three-dimensional topological graphs (Fig. 2c). The essential premise of reduction is that each platform requires at least two equivalent prismatic joints to maintain the closed-loop mechanism, i.e., each vertex is related to at least two edges in the topological graph, and then the original kinematic properties, including mobility and radial motion, should be reserved among polyhedral platforms. It is mathematically surprising to find that the Hamiltonian path (or Hamiltonian cycle) matches the premise of the reduction process. There are two significant characteristics of the Hamiltonian path: first, it is a closed-loop path with a sequence of edges that visits all the vertices of a graph; second, each vertex between two edges is only accessed exactly once along the path. For demonstration purposes, the generation process of the Hamiltonian path in a tetrahedron is taken as an example, as shown in Fig. 2d.

Fig. 2. Equivalent tetrahedral mechanism and its Hamiltonian path

        Next, the obtained Hamiltonian path, also given in Fig. 3a, can split the tetrahedron into two half shells, as shown in Figs. 3b and 3e. The half shell in Fig. 3b is an assembly of two 1-DOF triangular units ADC and ADB connected by one common edge AD, yet the overconstraints of this two-loop equivalent mechanism are c_e=2. Furthermore, to explore the possibility of the simplest constraint path, we can only remove edge AD under the mentioned reduction premise. Thus, a skew quadrilateral (nonplanar quadrilateral) ABDC is obtained in Fig. 3c with c_e=0. The equivalent kinematics of the four involved Sarrus linkages and the entire simplest tetrahedron can also be obtained. Hence, the skew quadrilateral ABDC can be regarded as the simplest constraint form, and the single-loop equivalent mechanism with four equivalent prismatic joints is given in Fig. 3d. Due to symmetry, the same reduction process can be conducted to obtain the simplest topological graph in Fig. 3f and the simplest equivalent mechanism in Fig. 3g, which are the same as Figs. 3c and 3d, respectively. Ultimately, by mapping the proposed simplest equivalent mechanism in Fig. 3d or 3g back to the original Sarrus-based mechanism, Fig. 4b shows the simplest tetrahedral mechanism integrated by four Sarrus linkages, in which the 1-DOF synchronized radial motion is preserved, and the actual overconstraint is greatly reduced from 19 to 7.

Fig. 3. Reduction process of the equivalent tetrahedral mechanism

Fig. 4. Original tetrahedral mechanism and its simplest form

        Without loss of generality, the construction method can be effectively applied to the deployable cubic mechanism (O_h symmetry) by involving twelve Sarrus linkages (Fig.5a). By using simplest quadrilateral unit and studying total two Hamiltonian paths of its dual octahedron, the only simple topological graph of the cubic mechanism can be identified in Fig. 5b. According to the simplest topological graph (skew quadrilaterals ABFC and ACDE connected by AC), the simplest one-DOF deployable cubic mechanism is obtained with the original motion behaviour of its platforms unchanged. Compared with the original cubic mechanism in Fig.5a, the actual overconstraints in this simplest Sarrus-based cubic mechanism are greatly reduced from 43 to 13.

Fig. 5. Original cubic mechanism and its simplest form

        The deployable dodecahedral mechanism (I_h symmetry) by involving thirty Sarrus linkages is constructed in Fig. 6a. There are a total of 17 distinct Hamiltonian paths on an icosahedron, which presents a different challenge to find all simplest constraint forms for this mechanism. Nevertheless, the proposed reduction method, including arranging the skew quadrilateral into basic units, can still be conducted for dodecahedral mechanisms. Considering an arbitrary Hamiltonian path as an example, as shown in Fig.6a in red lines, which connects all twelve vertices without any symmetry. One-DOF skew quadrilaterals ADIC, CILH, CHGB, BGKF and FKJE can be sequentially arranged inside the Hamiltonian path, leading to a one-DOF assembly of these five basic units, as shown in Fig. 6b. Similarly, if we further arrange five skew quadrilaterals CBFA, AFED, DEJI, IJKL and LKGH in the other half shell, another different simplest constraint path is obtained in Fig. 6c. Ultimately, by mapping the simplest topological graphs to the original Sarrus-based mechanism, the two simplest dodecahedral mechanisms that preserve the original 1-DOF radial motion, and the degrees of overconstraint in these simplest mechanisms are greatly reduced from 115 to 31. Therefore, 17 Hamiltonian paths of an icosahedron have been discussed in detail, and a total of 19 simplest constraint paths of this dodecahedral mechanism can be found and identified.

Fig. 6. Original dodecahedral mechanism and its simplest form

        Therefore, two papers were published on Mechanism and Machine Theory. The co-corresponding authors of the paper are Prof. Yan Chen from Tianjin University and Prof. Guowu Wei from University of Salford, the first author is Yuanqing Gu and the second author is Xiao Zhang from Tianjin University. This work establishes an approach for the design of novel DPMs based on spatial symmetries and proposes the overconstraint reduction strategy based on the Hamiltonian path. This research establishes a strong theoretical foundation for the innovative research of DPMs and provides effective technical support for their engineering applications.

1. Gu Y, Zhang X, Wei G*, Chen Y*. Sarrus-inspired deployable polyhedral mechanisms. Mechanism and Machine Theory, 2024, 193, 105564.
(https://doi.org/10.1016/j.mechmachtheory.2023.105564)
2. Gu Y, Zhang X, Wei G*, Chen Y*. Hamiltonian-path based constraint reduction for deployable polyhedral mechanisms. Mechanism and Machine Theory, 2024, 193, 105563.
(https://doi.org/10.1016/j.mechmachtheory.2023.105563)