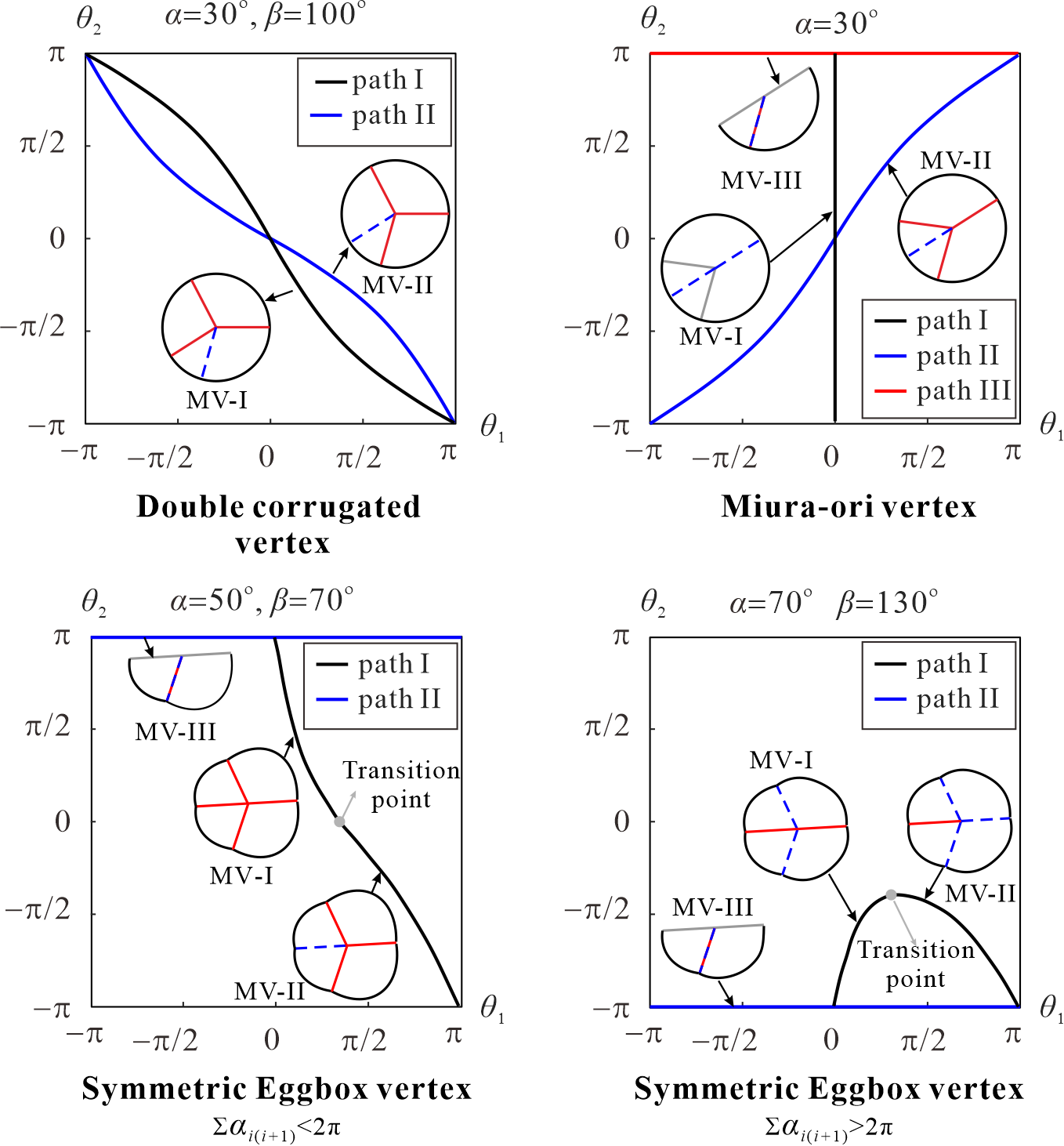
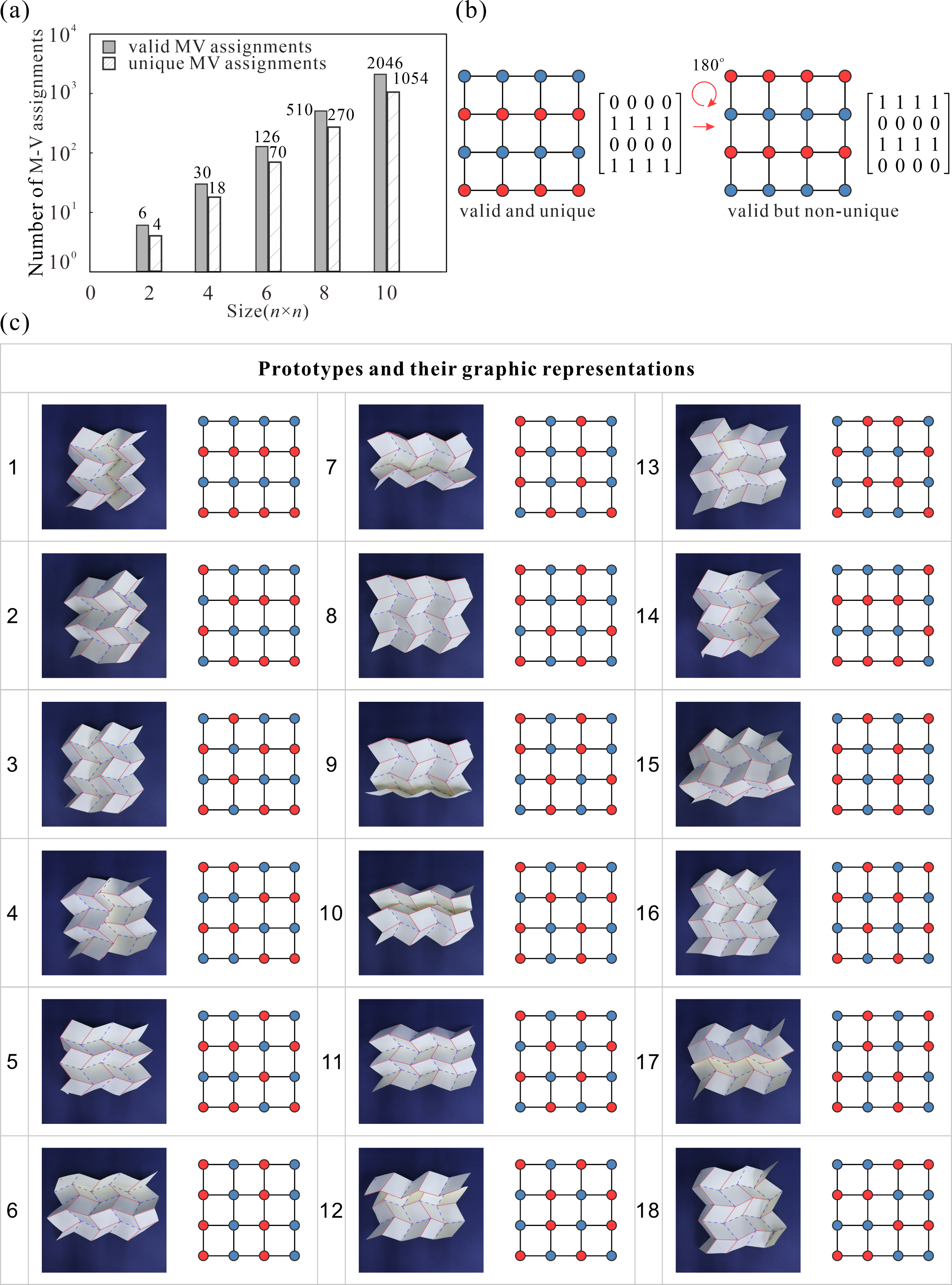
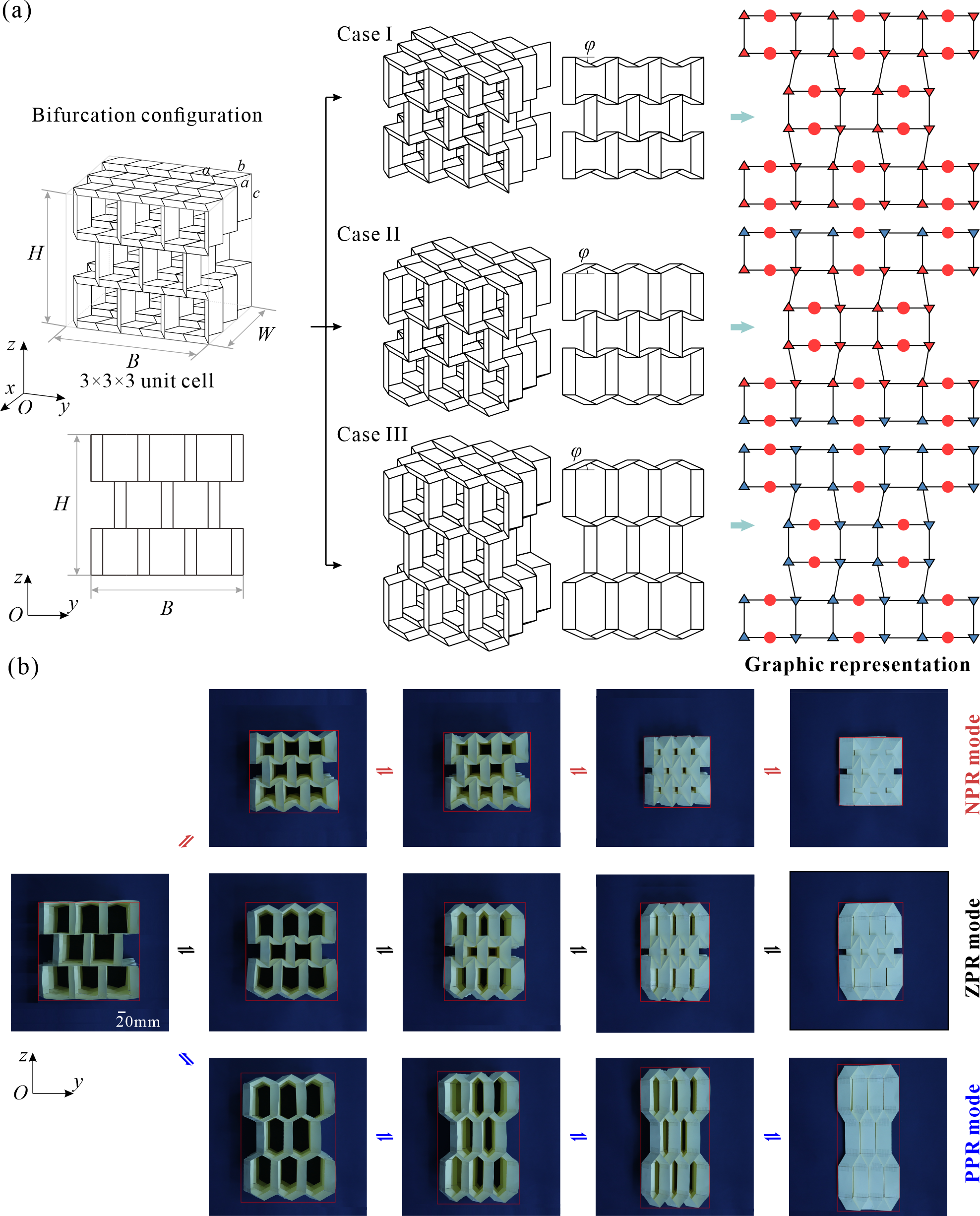
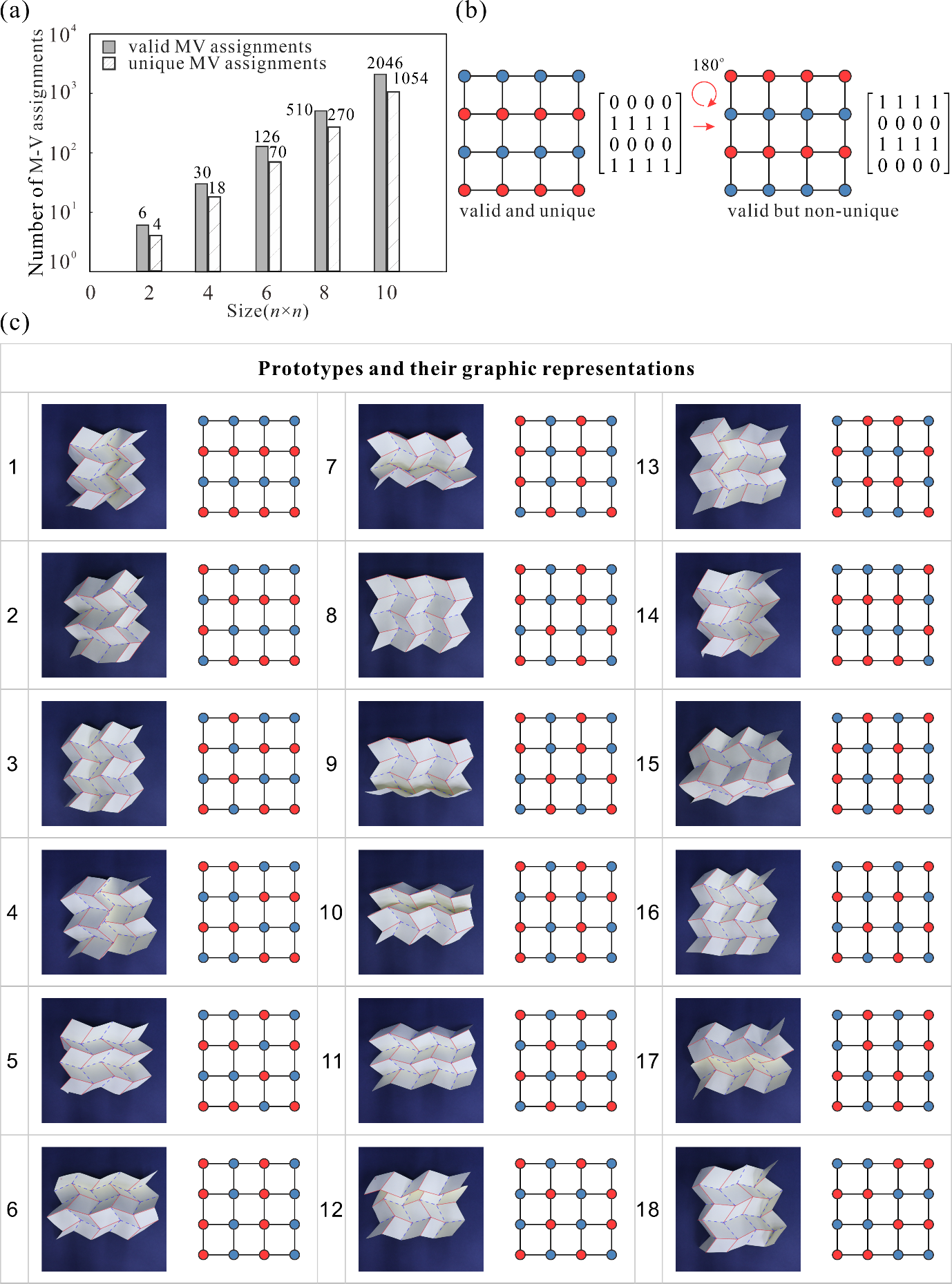
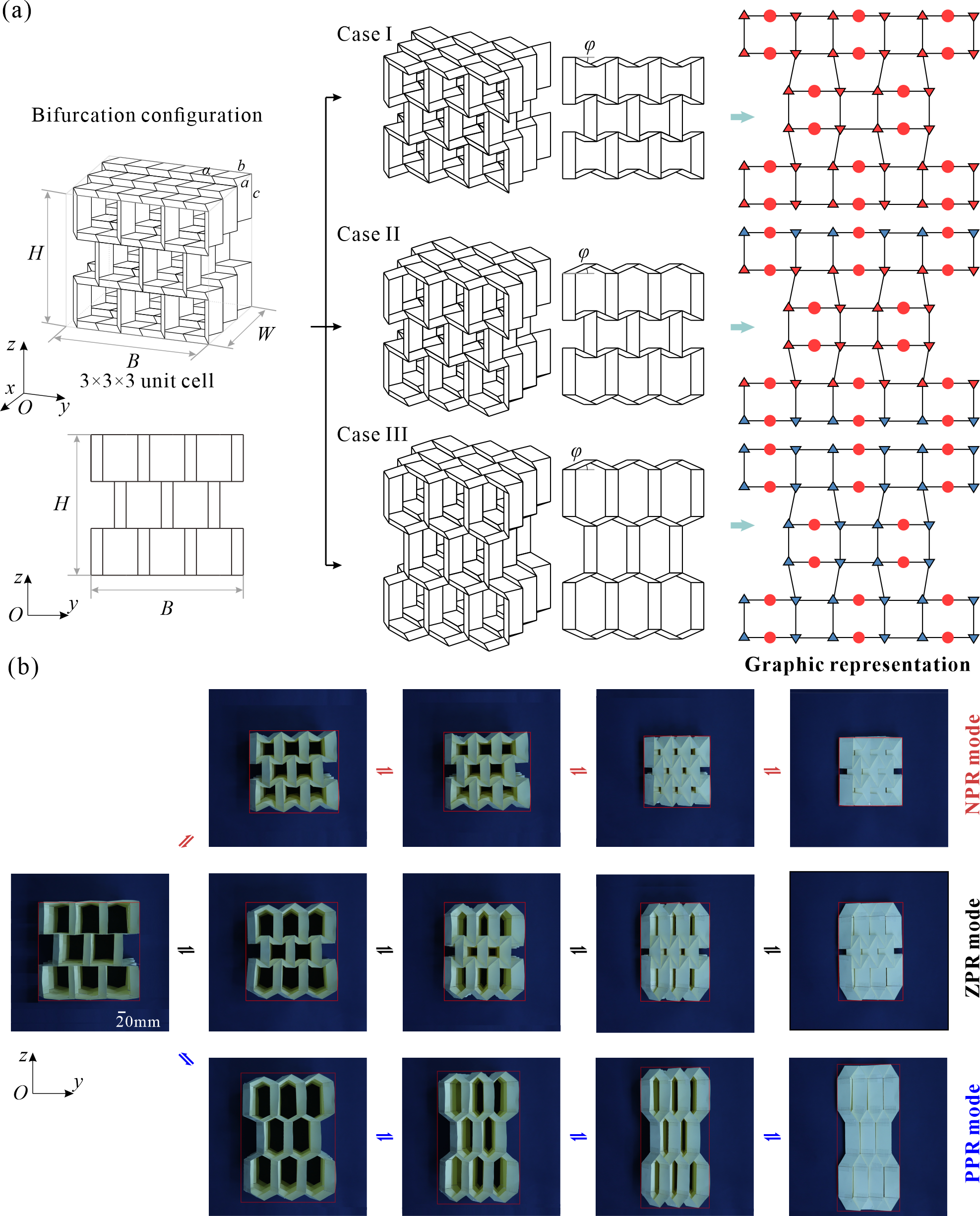
Rigid origami structures can be used to fold two-dimensional flat paper into complex three-dimensional three-dimensional structures by only rotating the creases without deformation of the panels, which has been widely used in the fields of spatial structures and mechanical metamaterials. Origami creases are usually classified as mountain creases (M) and valley creases (V), and their distribution directly determines the morphology of the origami structure. Once the process is completed, the position of the creases in the origami structure is uniquely determined. Therefore, conventional origami structures can only be transformed between a single folded and unfolded state. Recent studies have shown that reconfigurable origami-inspired folding has recently gained significant attention due to its potential to achieve multi-shape changes through crease topological morphing, resulting in multi-functionality from a single original structure. However, among the large number of rigid origami patterns, it is still open questions about which patterns can be reconfigured and how many reconfigurations are possible. Therefore, it becomes particularly important to determine all possible mountain-valley crease (MV) assignments that ensure rigid foldability and obtain duplicate configurations in large 2D origami tessellations or 3D cellular structures.
        Recently, the team of Professor Yan Chen of Tianjin University developed a straightforward algorithm that combines graphic representation and motion compatibility conditions to assess the reconfigurability of one-DOF origami structures with 4-crease vertices as well as their 2D and even 3D cellular tessellations. This work was published online on March 25th, 2024 in the International Journal of Mechanical Sciences. The corresponding author of the paper is Prof. Yan Chen of Tianjin University, the first author is Weiqi Liu, a PhD student at Tianjin University, and the second author is Song Cao, a master's student at the College of Intelligence and Computing, Tianjin University. The study was supported by the National Natural Science Foundation of China and New Cornerstone Science Foundation through the XPLORER PRIZE.

        Firstly, the topological change of the crease of a 4-crease origami vertex can be equated to the kinematic bifurcation of a spherical 4R linkage, and different MV assignments correspond to different bifurcation paths of the linkage. Therefore, by deriving the inverse closure equations of the spherical 4R linkage corresponding to the three most commonly used origami vertices, Miura, double corrugated and eggbox, the mapping from kinematic paths of origami vertices to mountain-valley crease assignment is established, as shown in Fig. 1.

Fig. 1 The mapping from kinematic paths of origami vertices to mountain-valley crease assignment.

        Subsequently, as shown in Fig. 2, the mountain-valley creases of different origami vertices are distinguished by shapes and colours and expressed in a binary computer language. For example, the double corrugated origami pattern has a 0 for MV I (blue circle) and a 1 for MV II (red circle). Taking inspiration from the concept of modularity, a single loop unit, encompassing several 4-crease vertices, is extracted as a module, and then the physical vertices and modules are translated into a graphic representation. The motion compatibility of assemblies of spherical 4R linkages is utilized to obtain rigid mountain-valley crease assignment of the origami loops formed by the 4-crease vertices. A rich graphical library of 18 typical modules with different geometric parameters is thus created. As can be seen, these modules cover both patterns consisting only of Miura, double corrugated and eggbox vertices, as well as patterns formed by mixing these vertices.

Fig. 2 Graphic representations of single vertex and eighteen typical modules

        If a purely kinematic approach to solving the motion compatibility condition for large 2D origami tessellations is still used to analyse the mountain-valley crease reconfiguration, it means that it is not only inefficient but also difficult to accurately identify all the bifurcation paths in a multi-loop linkage network. So, the origami tessellation is abstracted into a checkerboard. And the challenge of searching for MV assignments that satisfy rigid foldability in large 2D origami tessellations or 3D cellular structures is transformed into a chessboard colouring problem and employs the Depth First Search (DFS) algorithm for its solution (Figs.3 and 4). Taking the double corrugated pattern in Fig. 3 as an example, it consists of two types of modules (exactly modules 1 and 2 in Fig. 2(b)), one considered as the basic module and the other considered as the connection module to constrain neighbouring basic modules, which can be easily distinguished by the geometry of the central quadrilateral panel. The rules of basic and connected modules established according to the graphic representation and motion compatibility conditions prune the connections between nodes of any two adjacent layers, so the size of the search space is effectively reduced. At the end of the process, each valid node visit sequence discovered by the DFS algorithm allows us to turn it back to an origami pattern with a valid MV assignment.

Fig. 3 Algorithm design for origami tessellation with size m×n

Fig. 4 Pseudo-code of the algorithm

        Furthermore, an advantage of utilising the graphic representation and DFS algorithm is the ability to remove duplicates by assessing the symmetry of the matrix, as shown in Fig. 5. The proposed algorithm is examined with 2D tessellations of different 4-crease vertices.

Fig.5 The search results for the number of valid MV assignments of a double corrugated pattern

        The proposed method can be extended to 3D cellular origami structures with more complex shapes and richer configurations. For a simple 3×3×3 tessellation in Fig. 6, it is surprising that 6642 valid configurations exist. In our discussion of these specific examples discovered during the exploration process, three typical graphic representations are presented in Fig. 6(a) right. When the origami pattern satisfies these mountain-valley crease assignments, it exhibits negative, zero and positive in-plane Poisson's ratio under large deformation, which is verified qualitatively and quantitatively by the kinematic model and DIC experiments.

Fig. 6 Typical configurations and motion modes of the 3×3×3 tessellation.

       In summary, a straightforward algorithm that combines motion compatibility conditions and graphic representation is developed to accurately assess the mountain-valley crease reconfiguration and obtain duplicate configurations in origami structures with 4-crease vertices and their tessellations. This research provides a strong theoretical foundation and technical support for the design of multifunctional structures based on mountain-valley crease reconfiguation.

Liu W, Cao S, Chen Y*. Mountain-valley crease reconfiguration of 4-crease origami vertices and tessellations. International Journal of Mechanical Sciences, 2024, 273, 109224.
(https://doi.org/10.1016/j.ijmecsci.2024.109224)