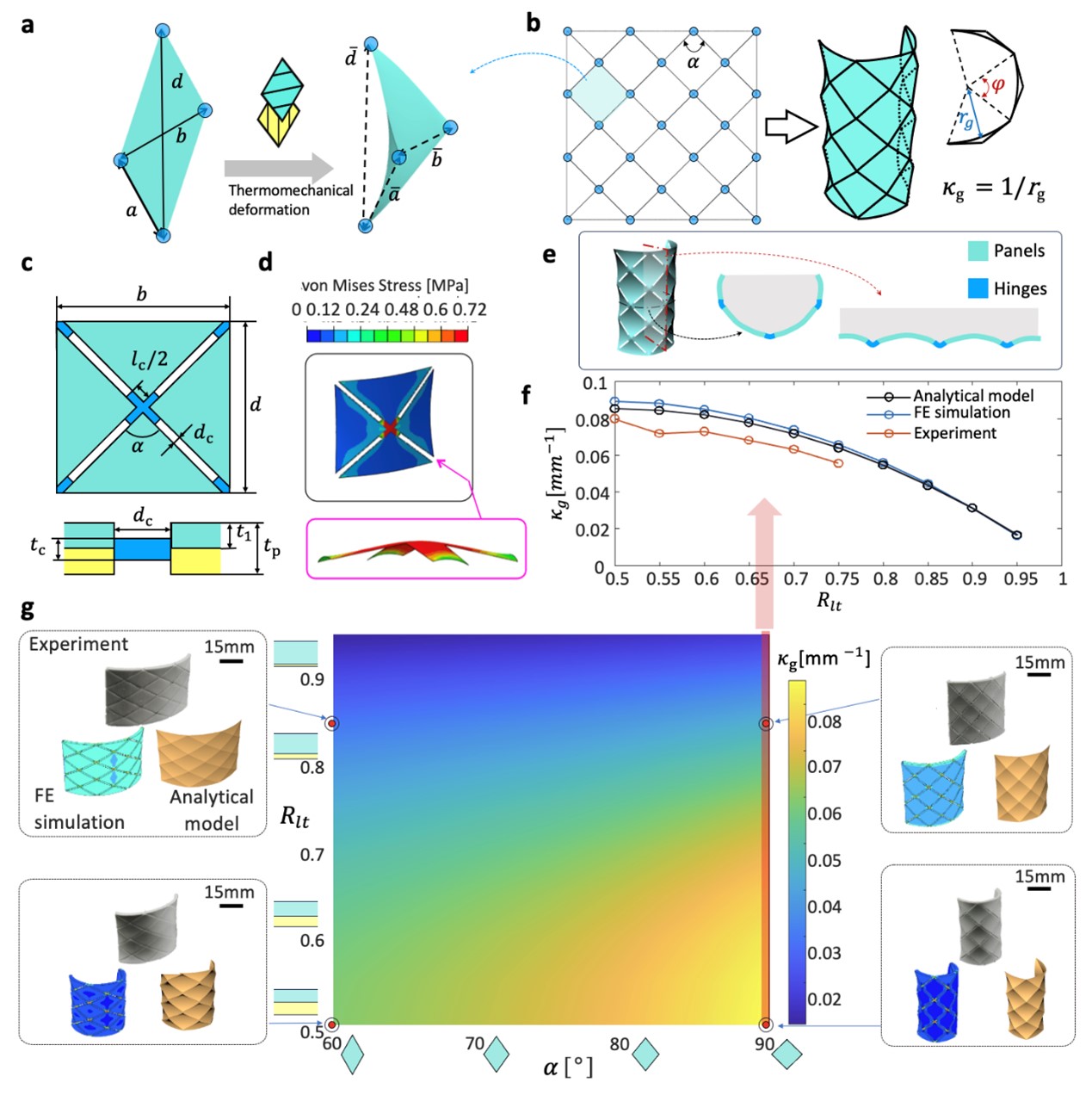
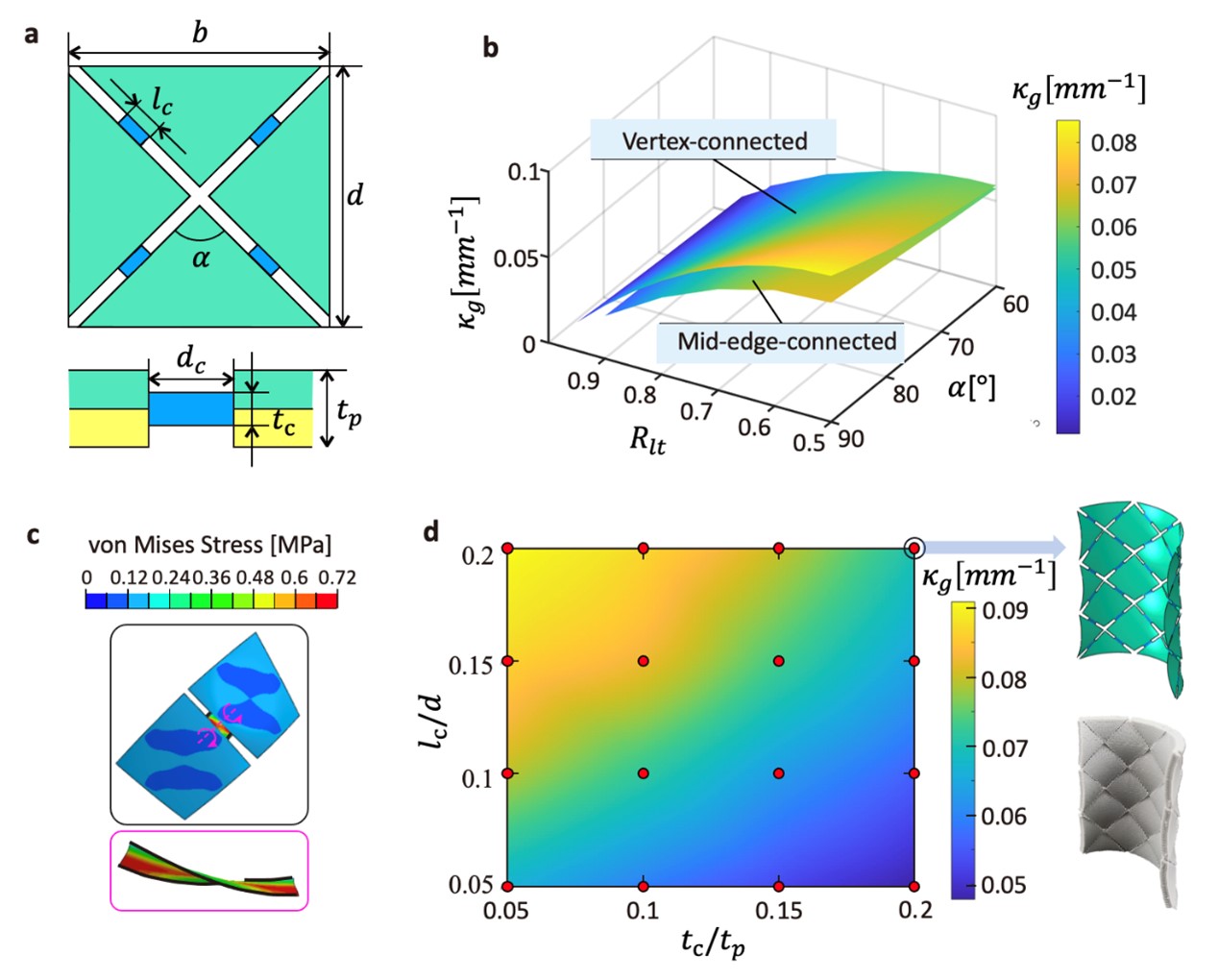
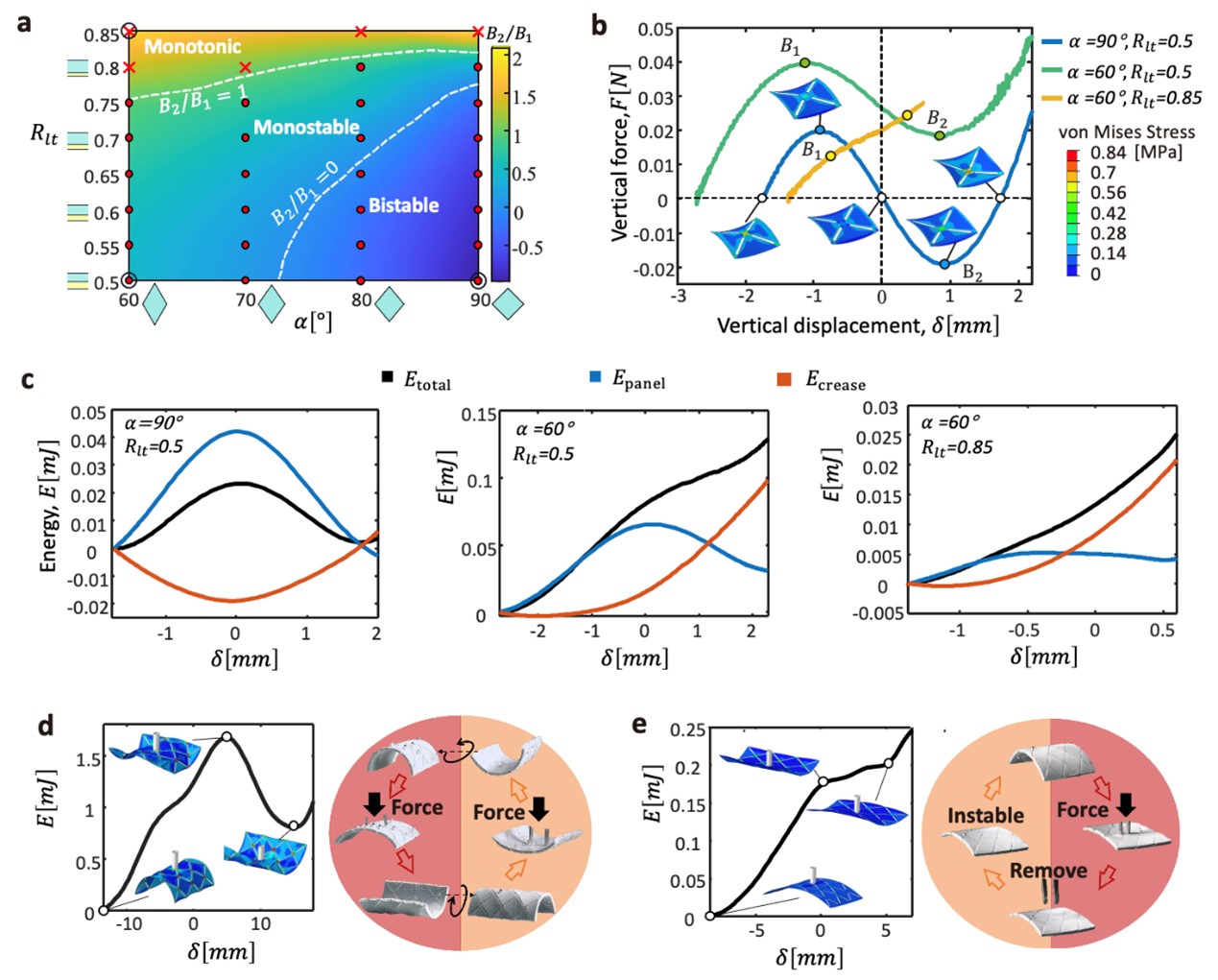
Non-Euclidean surfaces are ubiquitous in numerous engineering fields, such as automotive, aerospace, and biomedical engineering. Origami structures, with their inherent ability to morph from two-dimensional planes to three-dimensional surfaces, have been extensively researched and utilized in the design and manufacturing of morphing surfaces. However, the current one-dimensional hinge deformation-driven transformation of foldable origami with rigid or slightly deformable panels cannot achieve a complex and large curvilinear morphing. Moreover, most active origami structures use thin hinges with soft materials, thus resulting in a lower load capability.
        To address this issue, a collaborative research effort was conducted by Prof. Jaehyung Ju's group at the University of Michigan - Shanghai Jiao Tong University Joint Institute, Prof. Jiayao Ma's group at Tianjin University, and Prof. Ke Liu at Peking University. The researchers utilized direct 4D printing of shape memory polymers to control and program tensorial anisotropic residual stress in origami panels. This novel approach allowed for printing panel deformation-driven origami structures with multi-modal deformations, enabling the morphing of non-Euclidean surfaces with large curvatures and high structural load capacity. The research findings have been published online in Advanced Intelligent Systems. The corresponding authors of the paper are Prof. Jaehyung Ju from the University of Michigan - Shanghai Jiao Tong University Joint Institute, and Prof. Jiayao Ma from Tianjin University. The co-first authors are Ph.D. student Zihe Liang at Shanghai Jiao Tong University and Ph.D. student Sibo Chai at Tianjin University.

        Instead of existing origami structures that use hinge deformation with simple folding modes to create discrete geometries with large deformation, the researchers proposed a panel deformation-driven approach to design the morphing of origami panels, thereby generating complex non-Euclidean surfaces. This panel deformation can be implemented using 4D printing by extruding the filaments of shape memory polymers. Leveraging the concept of the shape memory effect, tensorial anisotropic residual stresses embedded through applying multilayer printing with varying filament orientations, thus enabling the programming of the panels morphing into desired geometric shapes. Specifically, by designing rhombic panels following a Yoshimura pattern with local negative Gaussian curvature, the structure can achieve an overarching cylindrical shape with global zero Gaussian curvature after heating. Furthermore, in addition to the inherent shape-fixity effect of shape memory polymers, this origami structure also exhibits structural locking due to its bistable behavior.

Figure 1 Self-folding origami manufacturing via panel deformation

        The researchers first analyzed the deformation characteristics of Yoshimura origami patterns in an in-plane tessellation with vertex connections. Based on the classical laminated plate theory (CLPT), the midplane strains and curvatures can be obtained by evaluating the effects of external resultant forces, moments, and thermal loadings on the bilayer laminated panels. The analytical results closely matched the deformations observed in experiments and numerical simulations, indicating that the thickness ratio of the bilayer laminated panels and the interior angles of the rhombic units significantly impact the overall bending curvature. Specifically, origami structures consisting of square units with two layers of equal thickness demonstrated the maximum curvature.

Figure 2 Thermomechanical deformation of a vertex-connected origami pattern

        In addition to the connection of the vertices, the researchers also investigated the topology effect of hinges located at the mid-edges of rhombic panels. Compared to the vertex-connected pattern, a mid-edge connection produces a lower bending curvature due to the hinge alignment along the off-principal curvature directions of deformed panels. The analysis revealed a torsional deformation mode occurring at the hinges, ensuring the continuity of the panel deformation along the non-principal curvature directions. Furthermore, the length and thickness of the hinges also affected the bending curvature, with longer and thinner hinges resulting in larger bending curvatures.

Figure 3 Thermomechanical deformation of an edge-connected origami pattern

        Researchers further analyzed the bistable characteristics of origami structures through parametric analysis, unveiling three distinct behaviors: bistable, monostable, and monotonic under different thickness ratios and rhombic angles. The strain energy ratio between the panels and the hinges played a crucial role in tuning the bistability, where the panel energy was determined by the orthogonality of the stresses in the bilayer rhombus units. Units with low orthogonality, characterized by a large thickness ratio and small rhombic angles, were dominated by strain energy of the hinges, resulting in monostable behavior. Conversely, units with high orthogonality, featuring equal thickness and a square shape, exhibited bistable snapping. Furthermore, multi-unit origami structures inherited mechanical properties from single units, showcasing bistable and monostable behaviors under different conditions.

Figure 4 The bistability of the origami structure

        The panel-driven 4D printing morphing method can be extended to a broader range of origami patterns to achieve varying curvilinear surfaces. By altering the printing and connection directions of the rhombic units and introducing combined designs for multimodal deformations, researchers further designed and printed origami patterns such as the maple leaf, wrapping, and mask. Upon heating, these structures underwent large curvature deformations following the predetermined modes, resulting in the formation of complex target surfaces. Additionally, the panel-driven origami does not significantly change in filling ratio after morphing, and the material shape-fixity effect ensures the high load capacity of these structures at room temperature.

Figure 5 Complex panel-deformation-driven morphing with multimodal deformation and high stiffness

Video 1 Panel-deformation-driven multimodal morphing

        In summary, this work introduces a novel panel-driven origami method for non-Euclidean shape morphing. The method showcases the self-folding deformation from various two-dimensional origami patterns to complex three-dimensional curvilinear shapes through direct 4D printing technology. Combining the unique shape fixity of shape memory polymers with the structural shape locking of mechanical bistability, the origami structures achieve reconfigurability and high load capacity. This provides a new approach for designing and manufacturing active origami structures capable of reversible, large curvature deformation, and shape locking.

Liang Z, Chai S, Ding Q, Xiao K, Liu K, Ma J*, Ju J*. Residual Stress-Driven Non-Euclidean Morphing in Origami Structures. Advanced Intelligent Systems. 2024, 2400246.
(http://doi.org/10.1002/aisy.202400246)