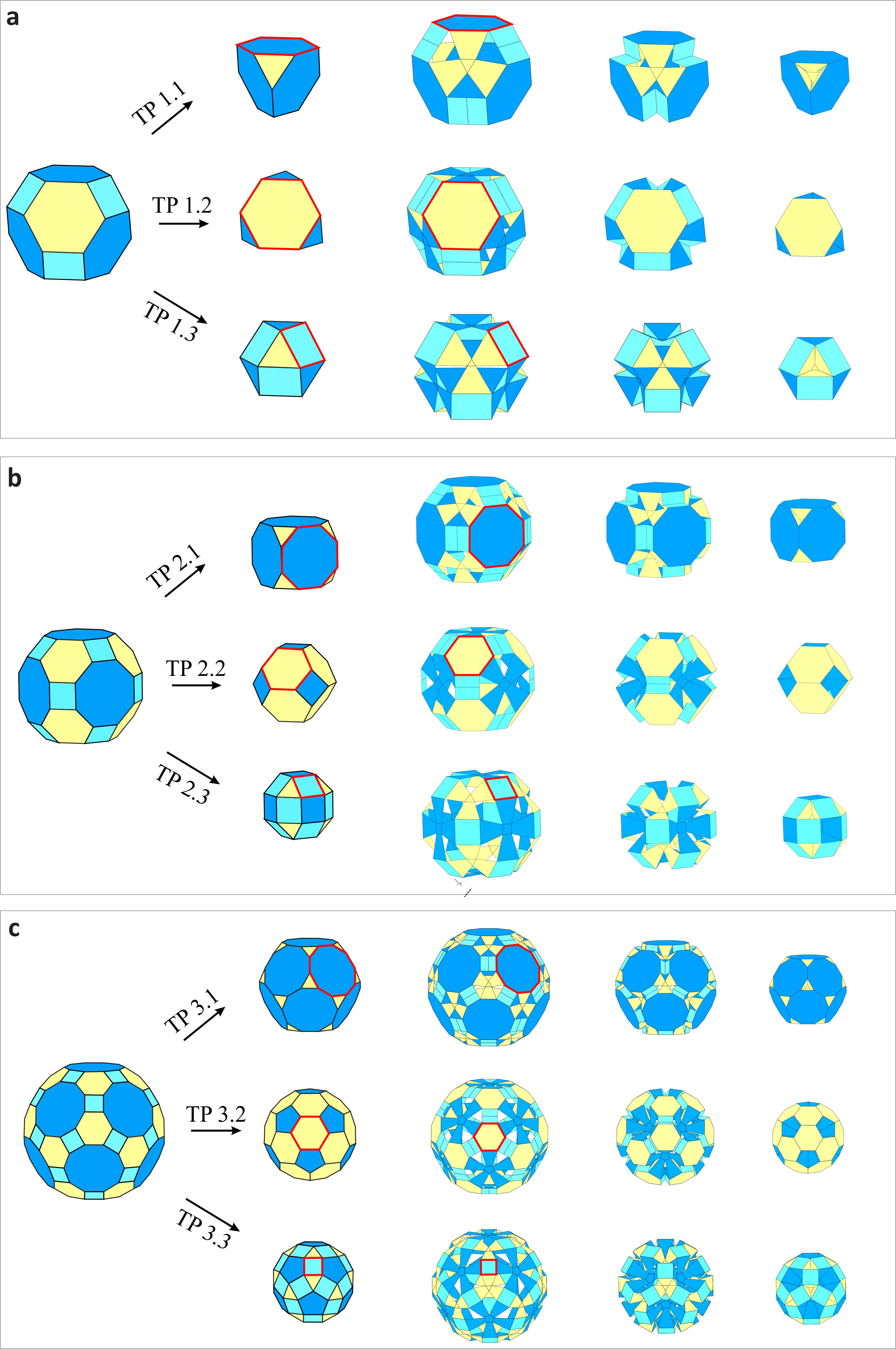
Transformable polyhedron is a special class of deployable polyhedrons that can achieve spatial configuration switching between two regular polyhedrons. Such designs require ingenious inspiration from solid geometry and mechanism kinematics, as well as research exploration of spatial symmetry. However, the pairing schemes in existing transformable polyhedron designs are relatively limited. It remains challenging to obtain diverse single-degree-of-freedom polyhedral transformation schemes using mechanism kinematic strategies.

         Recently, Professor Yan Chen from the School of Mechanical Engineering at Tianjin University, in collaboration with Professor Guowu Wei from the University of Salford, UK, proposed a series of kirigami polyhedrons based on spatial 7R linkages by exploring potential polyhedral transformation pairings in Archimedean solid geometry. This study achieved geometric symmetry transformations through kinematic strategies. The work was published online in Small Structures on September 23, 2025, with Professor Yan Chen as the corresponding author and Dr. Yuanqing Gu as the first author. The study was supported by the National Natural Science Foundation of China and New Cornerstone Science Foundation through the XPLORER PRIZE

        Researchers have introduced additional panels and creases into kirigami patterns based on spatial 9R linkages, achieving a single-degree-of-freedom threefold-symmetric kirigami pattern. Its kinematic model can be analogized as a threefold-symmetric spatial 7R mechanism network. Similarly, more spatial 7R mechanism networks can be constructed with multiple symmetries. Due to the translational properties of spatial 7R mechanism units, such mechanism networks exhibit single-degree-of-freedom synchronized motion. By embedding multi-symmetric mechanism networks as building units into Archimedean polyhedrons surfaces, such as the great rhombicosidodecahedron, great rhombicuboctahedron, and great rhombicosidodecahedron with their respective spatial symmetries, a series of kirigami polyhedral mechanisms based on spatial 7R mechanism networks have been developed (Figure 1）

Figure 1 kirigami polyhedral mechanisms based on spatial 7R mechanism networks

        Then, by selectively retaining one type of polygon while folding the other two among the three polygons composing an Archimedean polyhedron surface, more diverse single-degree-of-freedom polyhedral radial transformation schemes have been achieved. These are demonstrated in Figure 2 in order of tetrahedral symmetry (Td), octahedral/cubic symmetry (Oh), and icosahedral symmetry (Ih) (Movies 1-3).

Figure 2 The polyhedral transformation schemes with ‌tetrahedral symmetry (Td)‌, ‌cubic symmetry (Oh)‌, and ‌icosahedral symmetry (Ih)‌

Movie 1

Movie 2

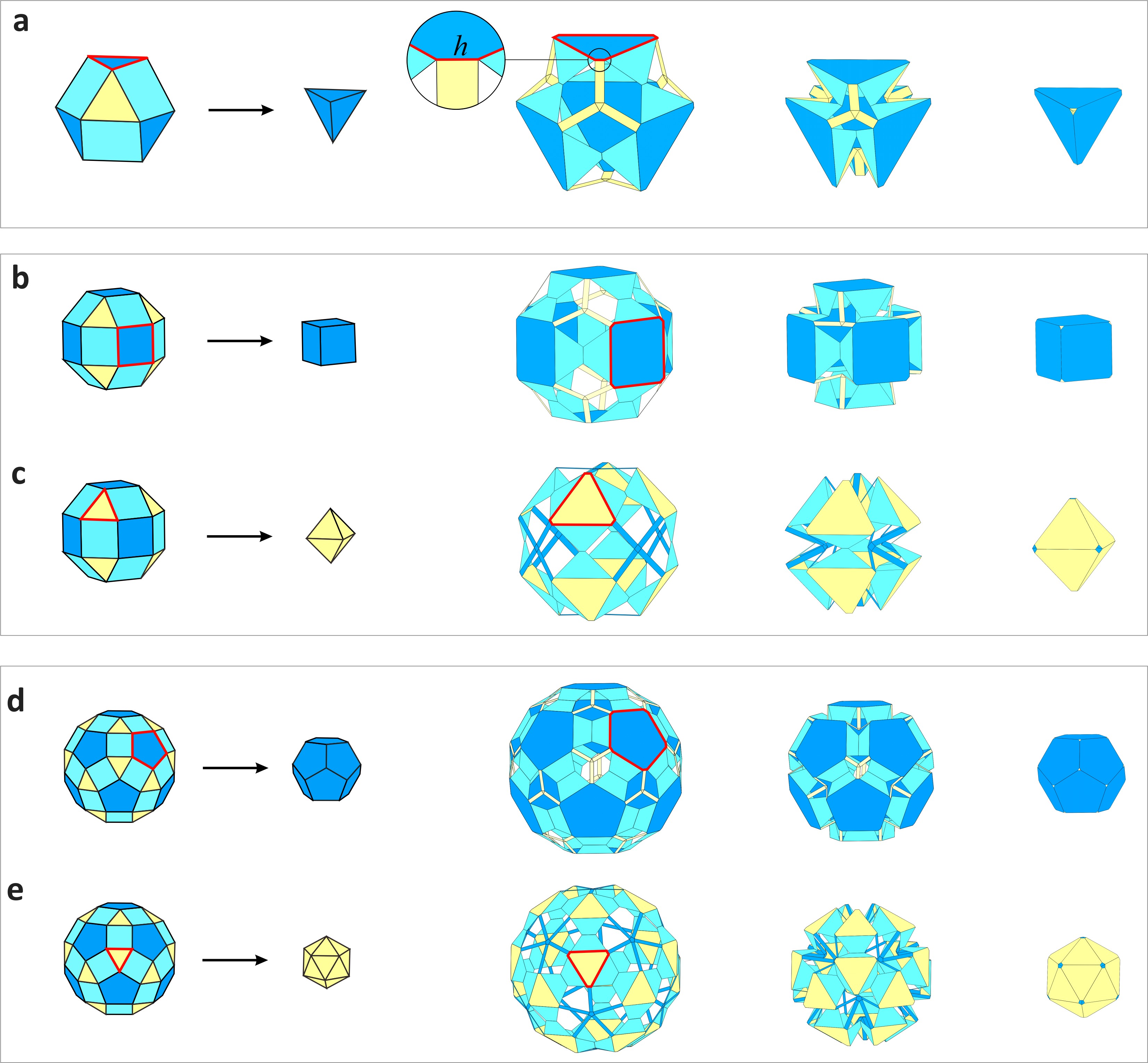
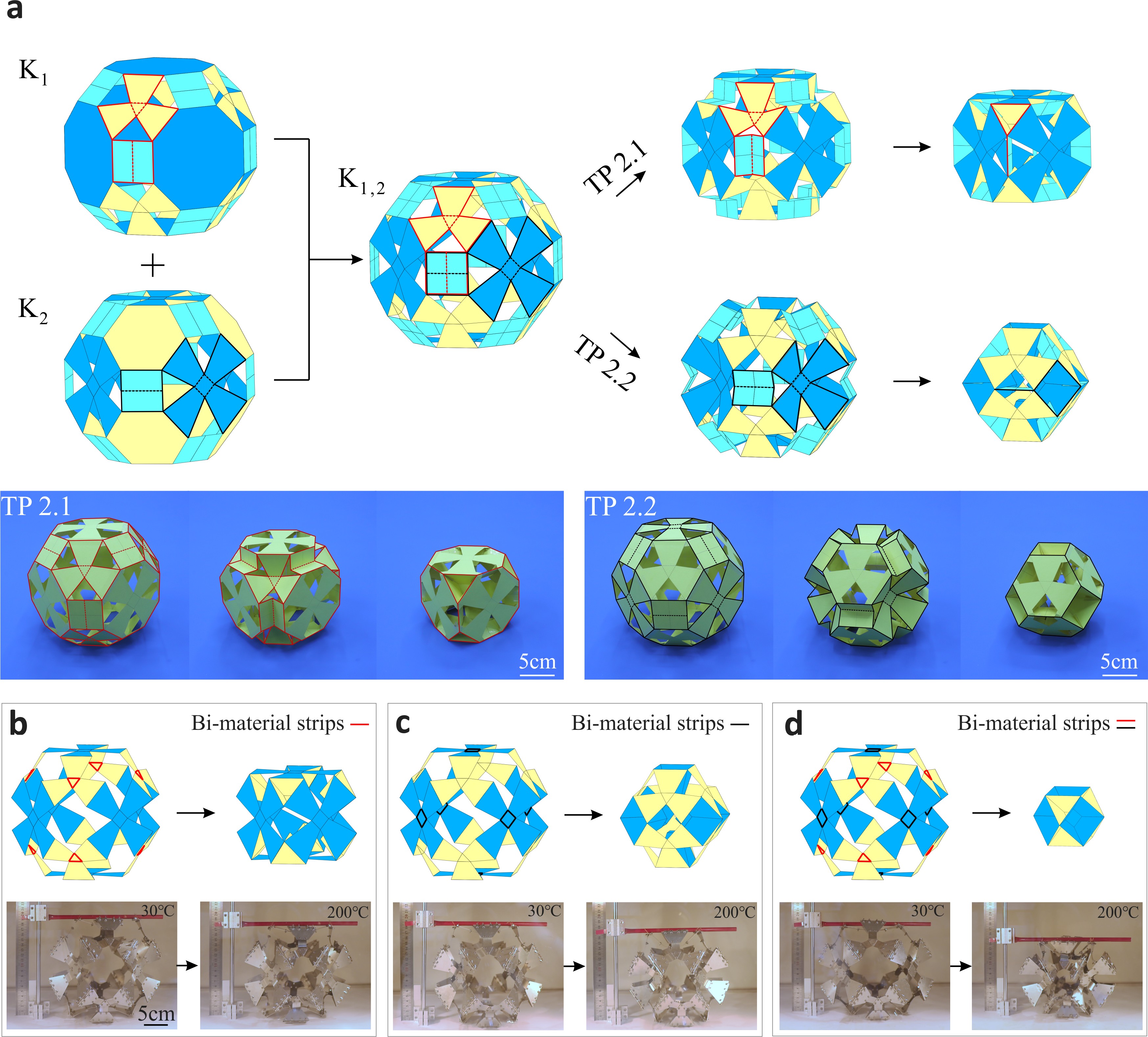
Movie 3

        Furthermore, based on the proposed kirigami polyhedron construction strategy and radial symmetry transformation principles, transformation schemes from Archimedean polyhedrons to Platonic polyhedrons can be explored by adjusting the geometric parameters of panels and creases (Figure 3). The mechanism topology remains a spatial seven-bar linkage network. So far, this study has identified five tetrahedral group transformation schemes, seven cubic group transformation schemes, and seven icosahedral group transformation schemes by leveraging the multi-symmetric spatial 7R mechanism networks among the eleven Archimedean polyhedrons and five Platonic polyhedrons.

Figure 3 Transformation schemes from Archimedean polyhedrons to Platonic polyhedrons

        Subsequently, taking the great rhombicuboctahedron as an example, two obtained crease patterns were superimposed to construct a reconfigurable kirigami polyhedron with two distinct folding pathways, each preserving the single-degree-of-freedom radial motion characteristics of the original patterns (Figure 4a, Movie 4). On the other hand, by removing the square panels with intersecting creases from the reconfigurable kirigami polyhedron and introducing bi-material strips as actuation creases, three polyhedral metamaterial cells with negative thermal expansion (NTE) were developed under different actuation layouts (Figure 4b-d). These unit cells all demonstrate orthotropic negative thermal expansion behavior (Movies 5-7).

Figure 4 Reconfigurable kirigami polyhedrons and polyhedral metamaterial cells with negative thermal expansion

Movie 4

Movie 5

Movie 6

Movie 7

        In summary, this study integrates stereometric geometry and kinematic mechanism theory to construct a series of kirigami Archimedean polyhedrons with one-degree of freedom radial transformation. It proposes comprehensive transformation schemes between Archimedean and Platonic polyhedrons while demonstrating their reconfigurability and thermal-responsive characteristics. The kirigami polyhedral mechanisms and transformation strategies presented in this work provide novel inspiration and design paradigms for innovative spatial deployable structures and multifunctional metamaterials.

Yuanqing Gu, Guowu Wei, Chuhan Xu, Yan Chen*. Kirigami Archimedean polyhedrons with one-degree of freedom radial transformation. Small Structures. 2025: e202500343.
(https://doi.org/10.1002/sstr.202500343)