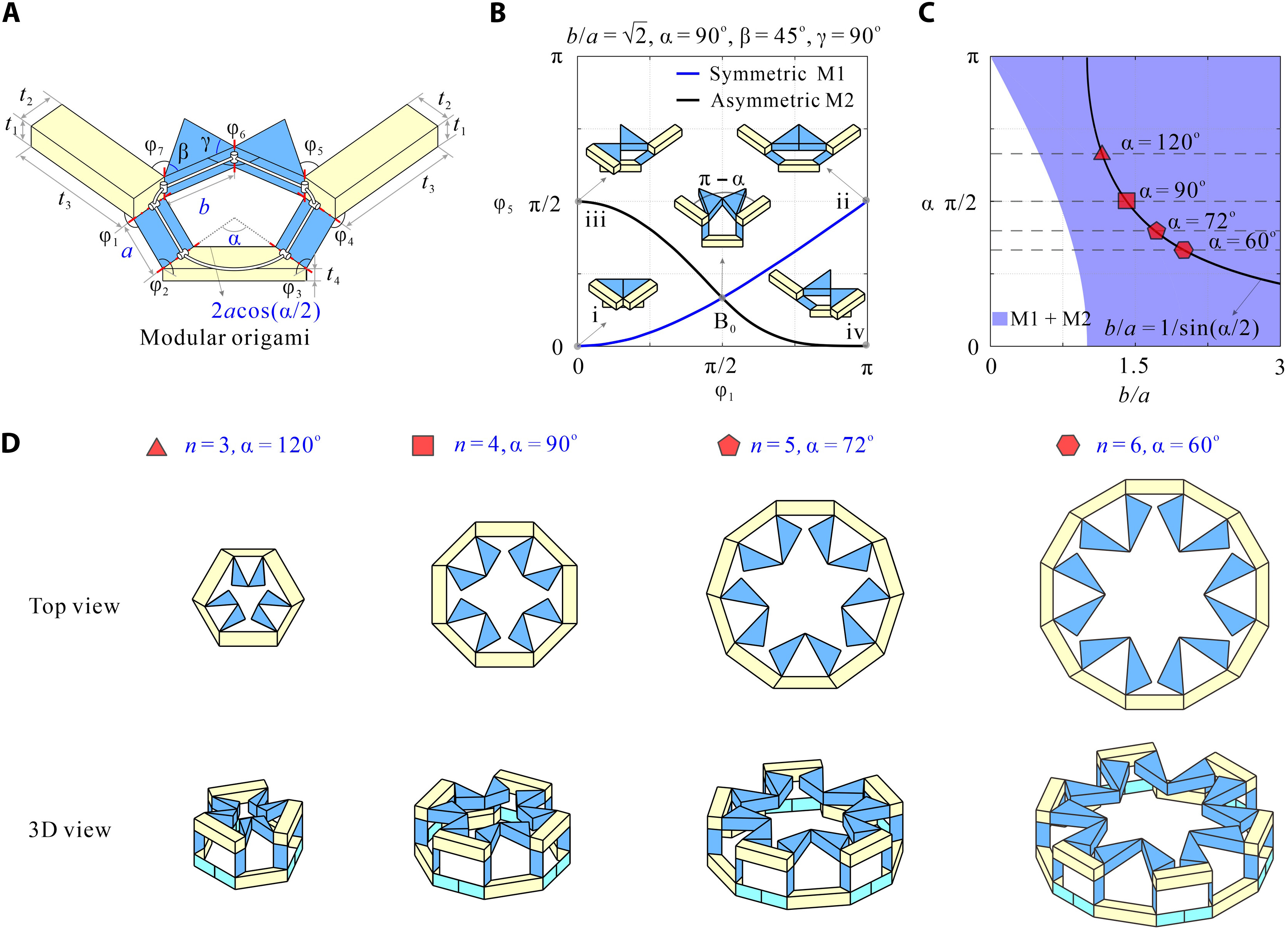
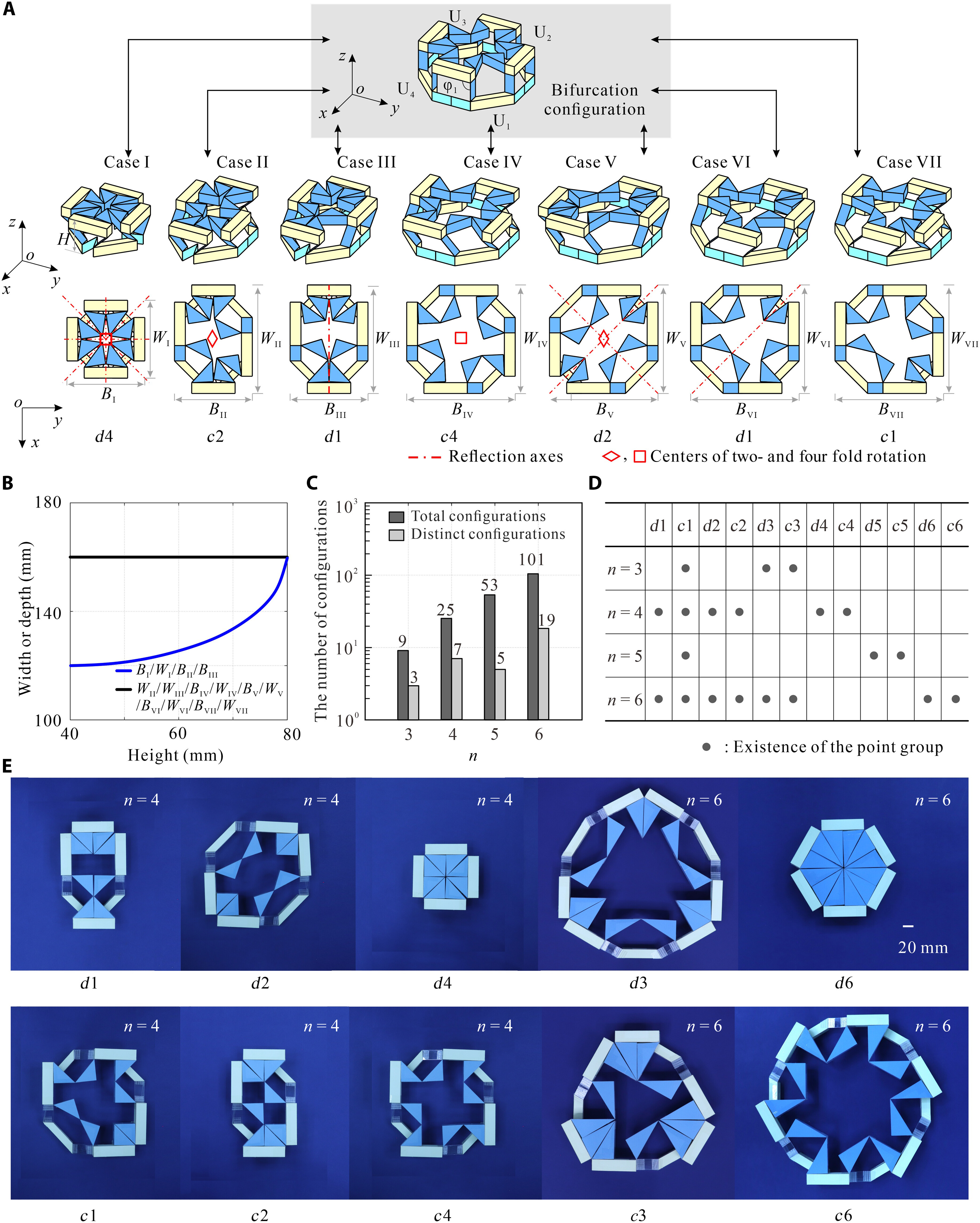
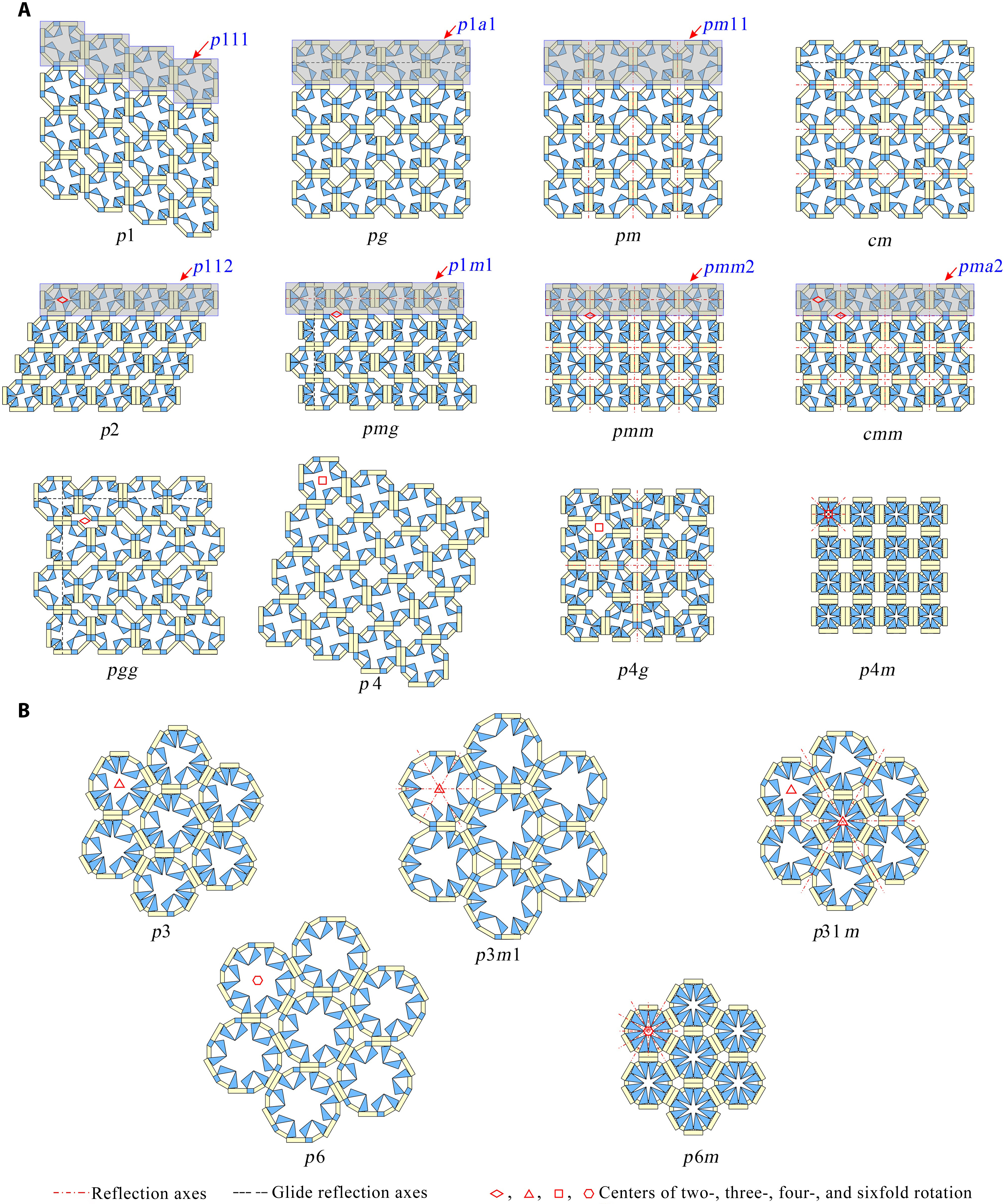
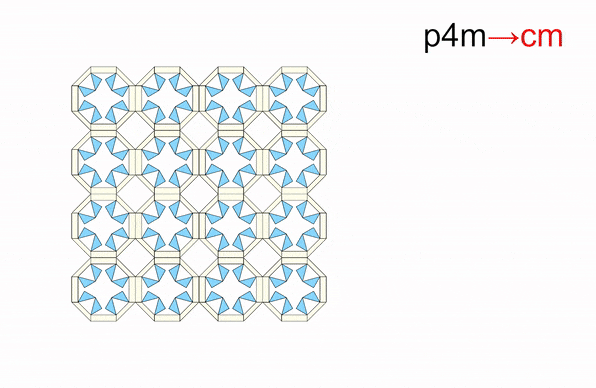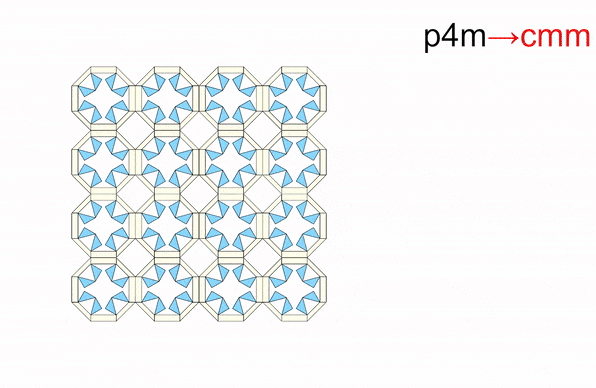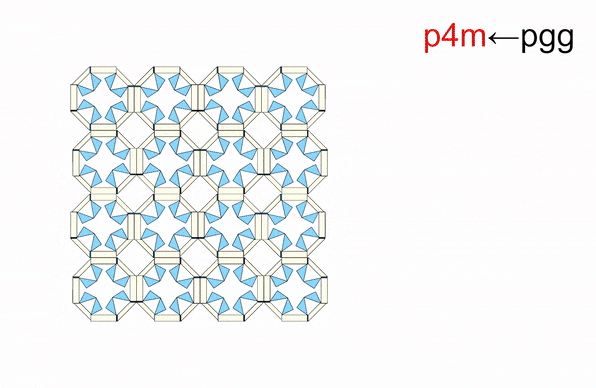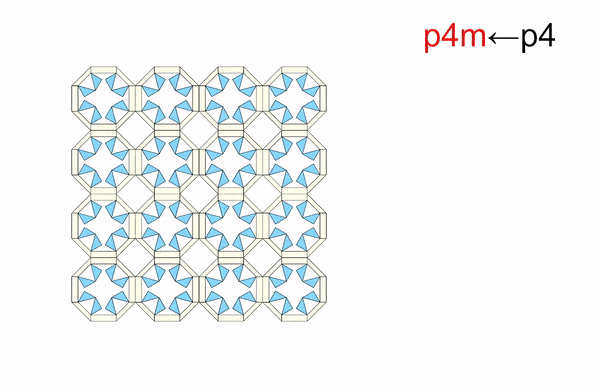
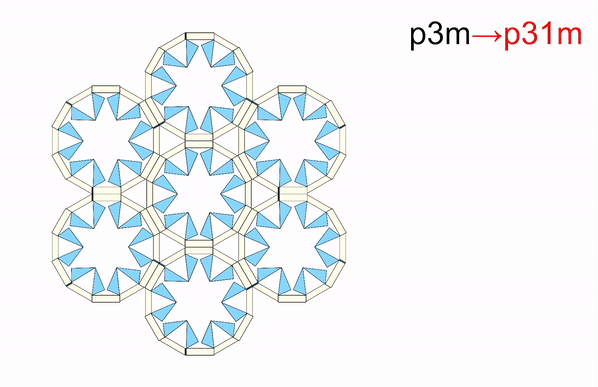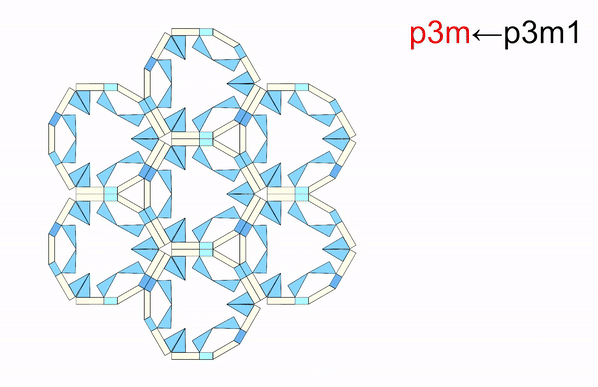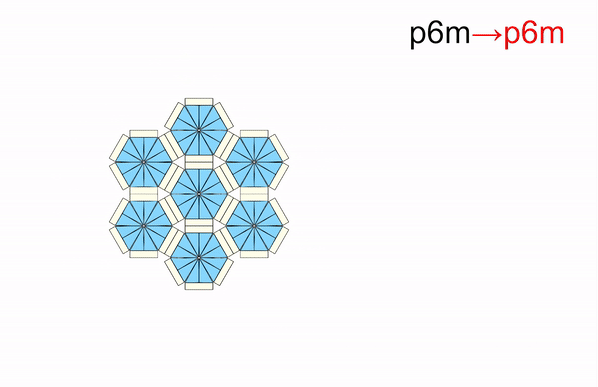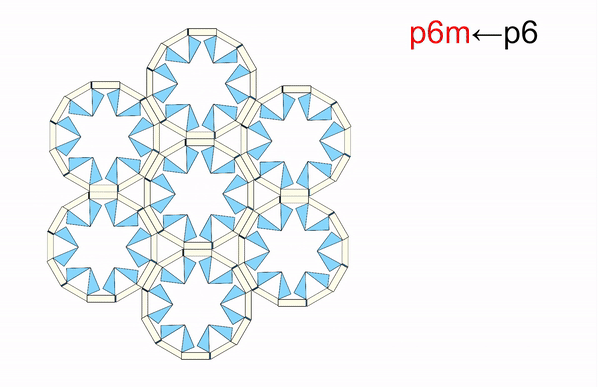
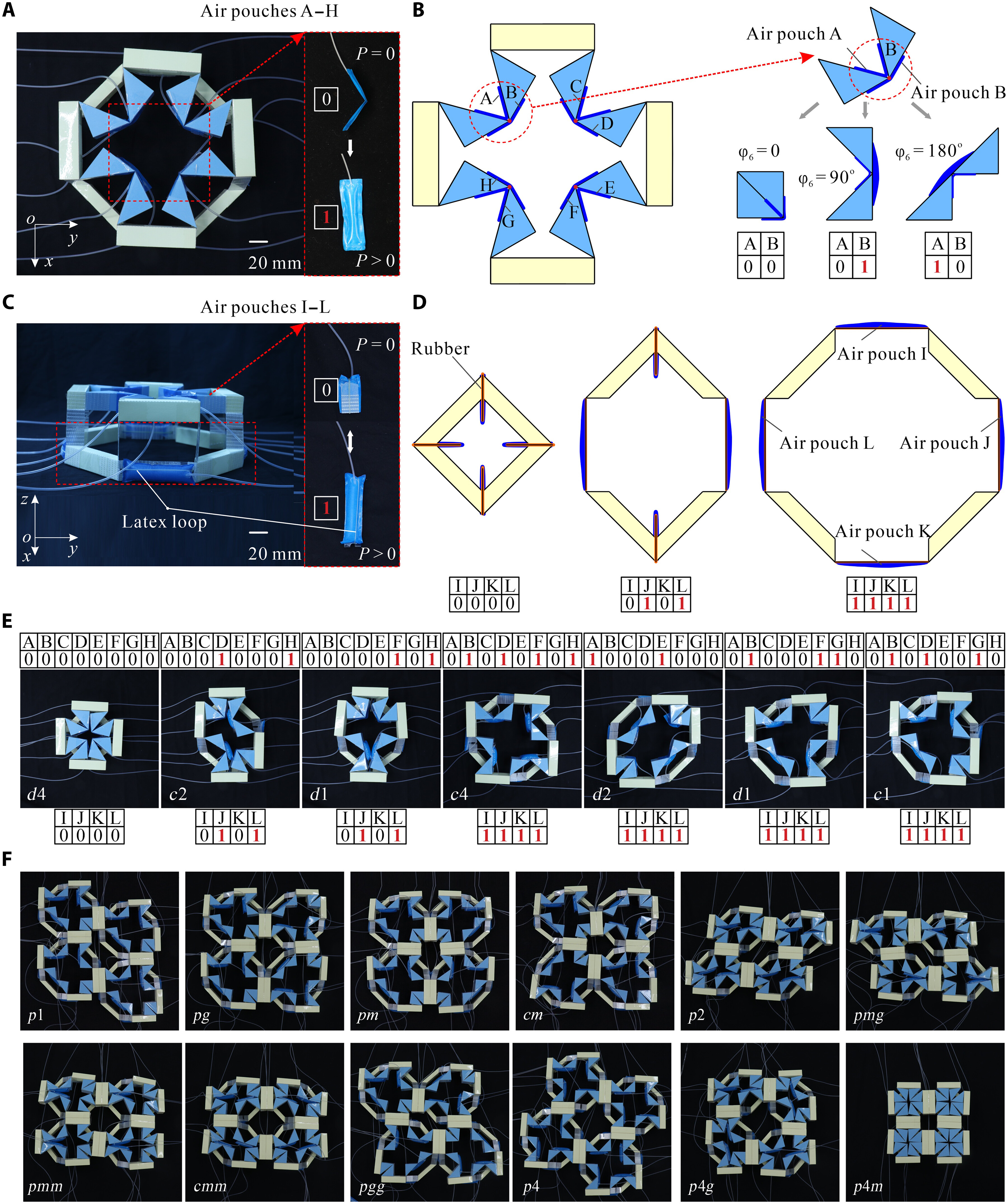
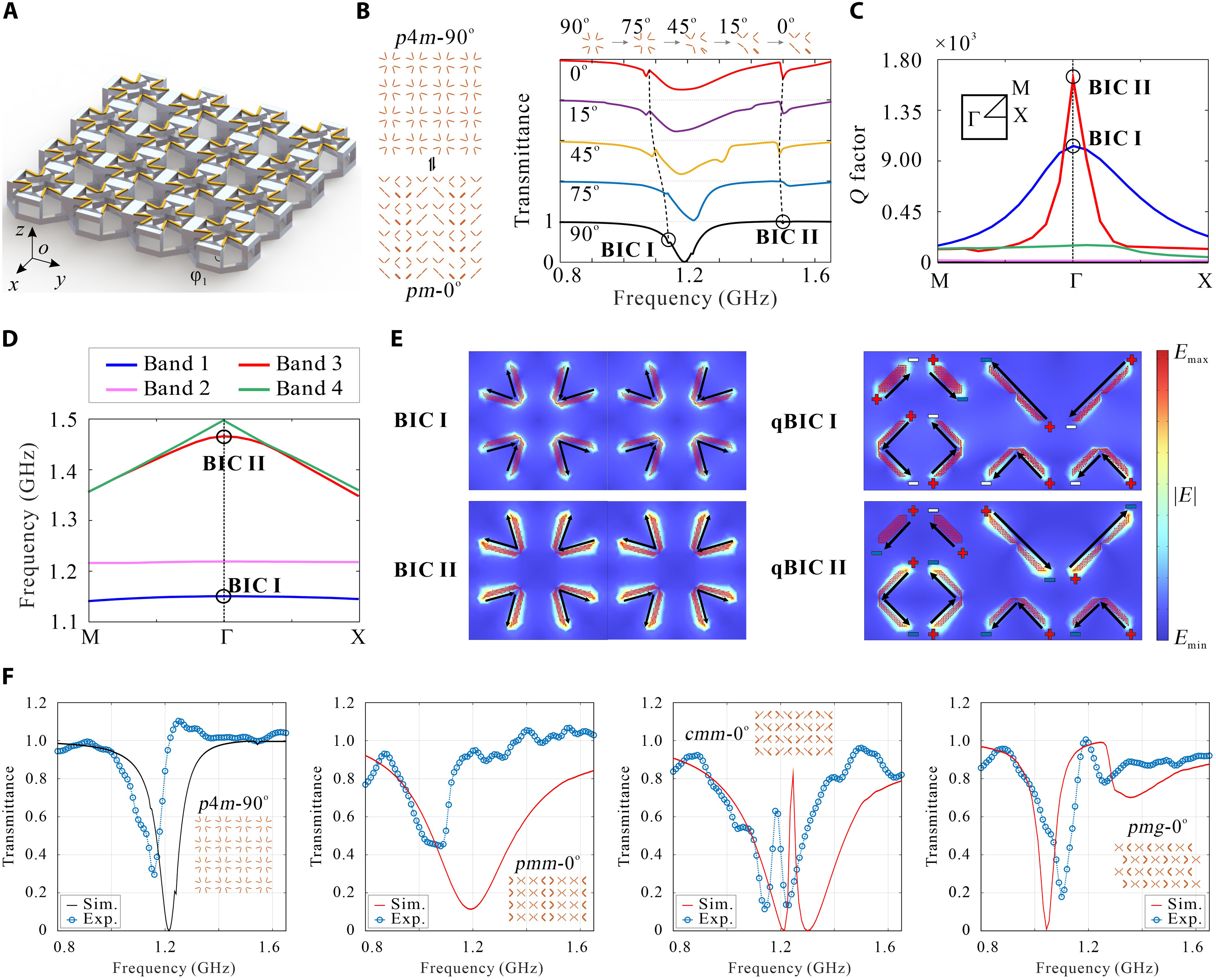
Symmetry is a ubiquitous phenomenon, deeply rooted in natural plants, animals, artificial architecture, Islamic motifs, and so on. On the Euclidean plane, there are only three classes of discrete symmetry groups in periodic structures, which encompass all transformations under which an object remains invariant. These three symmetry groups include two families of rosette groups (2D point groups), seven frieze groups (2D line groups), 17 wallpaper groups (2D space groups) in finite designs, mono-translational designs, and bi-translational designs, respectively. The presence of symmetry in geometric shapes not only contributes to their aesthetic appeal but also correlates with the physical properties in many fields, such as electromagnetics, optics, acoustics, etc., thus tunability among different symmetry groups is highly desired in the corresponding systems to achieve multiple functionalities. However, among the limited cases of altering symmetry motifs, the major methods rely on the refabrication or reassembly.

         Recently, the teams of Professor Yan Chen of Tianjin University and Professor Hanqing Jiang of Westlake University developed a set of modular origami with single degree-of-freedom and kinematic bifurcation that can be reconfigured into all 17 wallpaper groups. This pioneering work, titled “Reconfigurable modular origami for tunable 2D symmetry groups” was published online in Science Advances in 12 November 2025. The corresponding authors of the paper are Prof. Hanqing Jiang of Westlake University and Prof. Yan Chen of Tianjin University. The co-first authors are Weiqi Liu, a postdoctor at the School of Mechanical Engineering, and Qun Ren, an associate researcher at the School of Electrical and Information Engineering, Tianjin University. Professor Jiayao Ma of Tianjin University and Dr. Zhuang Zhang, a postdoctor at Westlake University, also made significant contributions to the research. This research was supported by the National Natural Science Foundation of China, the New Cornerstone Science Foundation through the XPLORER PRIZE, and the National key R&D Program of China. The paper was also selected as the Featured Image of the issue.

        The design of modular origami is fundamentally guided by the concept of kinematic bifurcation, where a mechanism can evolve into multiple motion paths due to its inherent geometric constraints. Linkages with kinematic bifurcations are usually accompanied by symmetric geometric parameters, and such bifurcation-induced reconfiguration often causes symmetry breaking in the configuration. To harness this characteristic, we constructed a plane-symmetric spatial 7R linkage specifically configured to support bifurcation (Figure 1). Then, the geometric parameters of the target spatial 7R linkage are mapped onto modular origami components, which are then sequentially assembled to realize the desired kinematic behavior, including bifurcations. when the two rectangular sheets are vertical at configuration B0, a kinematic bifurcation occurs, as revealed by closure equations of the 7R linkage. If two rectangular sheets swing in the opposite directions, the unit follows a plane-symmetric path M1. Conversely, if the sheets swing in the same direction, the unit involves asymmetric path M2. The kinematic analysis reveals that two rectangular blocks are always horizontally positioned and maintain angle π-α no matter moving along M1 or M2 path. Therefore, we can construct n-unit symmetry modules by arranging n modular origami units with α=2π/n in a circular array, where each pair of neighboring units shares a common rectangular block. To ensure that the mechanical assembly of n units retains a single DOF, two additional ice blue sheets, each with length a, are inserted between neighboring units to form a 7R closed loop with α=0. Eventually, a set of single-DOF n-unit (n=3, 4, 5, 6) symmetry modules is constructed.

Figure 1. Construction of n-unit (n=3, 4, 5, 6) symmetry modules using modular origami unit with kinematic bifurcation

        Due to the n-fold symmetry in the n-unit module composed of identical units, both the kinematic compatibility and bifurcation are well preserved. For the four-unit symmetry module in Figure 2, the top configuration is the bifurcation point as four modular origami units with α=90o are all in the bifurcation configuration, i.e., each of them can choose to move either in the M1 or M2 path. There are a total of 25 cases that satisfy kinematic compatibility conditions for the four-unit symmetry module, but due to the similarity of the orthogonal directions, there are only seven different bifurcation configurations, and six types of point groups, i.e., d4, c4, d2, c2, d1, and c1 point groups. We also investigated kinematic bifurcation and symmetry changes for three-, five-, and six-unit symmetry modules. Specifically, the three-unit symmetry module exhibits d3, c3, and c1 point groups, the five-unit symmetry module exhibits d5, c5, and c1 point groups, while the six-unit symmetry module exhibits d6, c6, d3, c3, d2, c2, d1, and c1 point groups Owing to powerful kinematic bifurcation, four- and six-unit symmetry modules are sufficient to cover all ten 2D crystallographic point groups, i.e., d1, d2, d3, d4, d6, c1, c2, c3, c4, c6, which are demonstrated by prototypes in Fig. 2E.

Figure 2. Reconfigurable n-unit symmetry module with tunable 2D point symmetry groups.

        Building on the reconfigurable symmetry modules, we systematically explored their ability to tessellate and realize all seven frieze groups and 17 2D wallpaper groups within a unified design framework (Figure 3). By applying consistent geometric connection rules. i.e., merging rectangular blocks while tuning local bifurcation states, we demonstrated a metastructure capable of accessing multiple symmetry groups through reconfiguration. Using only the 4-unit symmetry module in a linear tessellation, all seven frieze groups (p111, p1a1, pm11, p1m1, p112, pma2, pmm2) were reproduced, each derived from identical module connections but distinct local operations such as translation, reflection, or glide reflection. The resulting seven patterns can be interconverted via local bifurcation-induced reconfiguration. Extending to two-dimensional periodicity, 12 of the 17 wallpaper groups with one-, two-, and three-fold rotational symmetries were systematically constructed by stacking or combining the seven frieze patterns. For instance, under the condition of merging rectangular blocks, the p1, pg, and pm wallpaper groups are obtained by vertically stacking the frieze patterns p111, p1a1, and pm11, respectively, in an orderly fashion. On the other hand, fourfold wallpaper patterns can be realized by combining motifs with lower symmetry using combinatorial operations or by directly using motifs with higher symmetry. Higher-order patterns (p4g, p4, p4m) were realized using modules with c2, c4, or d4 symmetry. All twelve groups share identical module connections and are thus physically realizable in one structure (Gif 1). The remaining five wallpaper groups (p3, p3m1, p31m, p6, p6m) requiring three- or six-fold rotation were achieved using three-unit or six-unit modules. A beehive tessellation of six identical modules surrounding a central one enabled p3, p3m1, p6, and p6m symmetries depending on the center module’s point group. The p31m group was constructed with alternating c3 and d6 modules (Gif 2). Together, the full set of 17 2D space groups can be comprehensively realized using only two modular systems: either the combination of three- and four-unit modules or the combination of four- and six-unit modules.

Figure 3. 2D line and space groups constructed by the 4-unit and 6-unit symmetry modules.

Gif 1. Wallpaper groups constructed by 4-unit symmetry modules.

Gif 2. Wallpaper groups constructed by 6-unit symmetry module.

        To realize programmable and reversible symmetry transformations, we implemented a dual-layer pneumatic actuation system for the one-DOF origami modules. The upper layer comprises eight air pouches (A–H) acting as symmetry selectors, and the lower layer includes four pouches (I–L) functioning as deployment actuators. Binary pressurization (“1” = inflated, “0” = deflated) controls hinge motion and global configuration. Specific actuation codes correspond to different symmetry states: for instance, “00010001,0101” and “00000101,0101” generate c2 and d1 point groups, while “01010101,1111” or “10001000,1111” yield c4 and d2 configurations. The system achieves reliable reconfiguration within seconds, with strong robustness to synchronization imperfections due to kinematic constraints and compliance in material joints (Gif 3). Moreover, the compliant structure allows transition pathways beyond ideal linkage kinematics, enabling reversible reconfiguration among non-bifurcated states and continuous geometric transformations (e.g., compact-square → rectangle → expanded-square). Applying the same pneumatic logic to a 2×2 tessellation reproduced all twelve wallpaper configurations experimentally (Gif 4), confirming scalable symmetry control through simple binary actuation without feedback loops.

Figure 4. The symmetry tuned by pneumatic actuation.

Gif 3. Reverse actuation of a single 4-unit symmetry module starting from the compact d4 configuration.

Gif 4. Actuation of 2×2 tessellation of 4-unit symmetry modules.

        Leveraging the symmetry-tunable platform, we designed a plasmonic origami metasurface consisting of copper tetramers on an FR4 substrate. Starting from the fully symmetric p4m-90° configuration, progressive reduction of the dihedral angle φ₁ breaks symmetry to pm-0°, converting symmetry-protected bound states in the continuum (BICs) into quasi-BICs (qBICs).Electromagnetic simulations reveal two BICs (~1.15 GHz and ~1.50 GHz) with Q-factors of 1628 and 1032, which evolve into radiative qBICs as symmetry decreases. Band structures confirm splitting of degenerate BIC branches, while field distributions illustrate how destructive interference in the symmetric state suppresses radiation. Symmetry breaking lifts this restriction, producing leakage waves and asymmetric Fano-type resonances. Across twelve symmetry configurations, the results show that high-symmetry (e.g., p4m, pmm) structures yield strongly trapped BICs with narrow single peaks, while chiral or mirror-chiral groups (p1, p2, cmm, p4g) support multiple deep narrow-band resonances. Glide-reflection groups (pg, pmg, pgg) exhibit only weakly confined, broad-band qBICs. Experimental transmission spectra from fabricated prototypes (p4m-90°, pmm-0°, cmm-0°, pmg-0°) agree well with simulations, validating the symmetry-governed selection rules. Minor deviations stem from finite-array effects and edge scattering. Overall, symmetry tuning enables precise control over electromagnetic confinement and coupling, offering a pathway toward multifunctional metasurfaces for sensing and filtering.

Fig. 5. Motion-sensitive multipole of plasmonic qBICs.

        In summary, this work has presented a novel approach to achieve active tunable symmetry groups in reconfigurable structures via inherent kinematic bifurcation behavior of single-DOF origami module metasurface, and demonstrated its potential application in high electromagnetic selection with multipole qBICs via antenna-integrated plasmonic metasurfaces. The 17 symmetry groups within a unified design framework proposed in this paper can be used as a cornerstone to deeply explore the intrinsic correlation between symmetry and multi-physical properties of electromagnetics, optics, acoustics, etc., which may lead to the establishment of a new theoretical framework of interdisciplinary integration.

Weiqi Liu#, Qun Ren#, Yunjie Wang, Zhuang Zhang, Xiuyu Wang, Yongshan Liang, Hao Huang, Jiayao Ma, Hanqing Jiang*, Yan Chen*. Reconfigurable modular origami for tunable 2D symmetry groups, Science Advances, 2025, 11, eady3812.
(https://www.science.org/doi/10.1126/sciadv.ady3812)