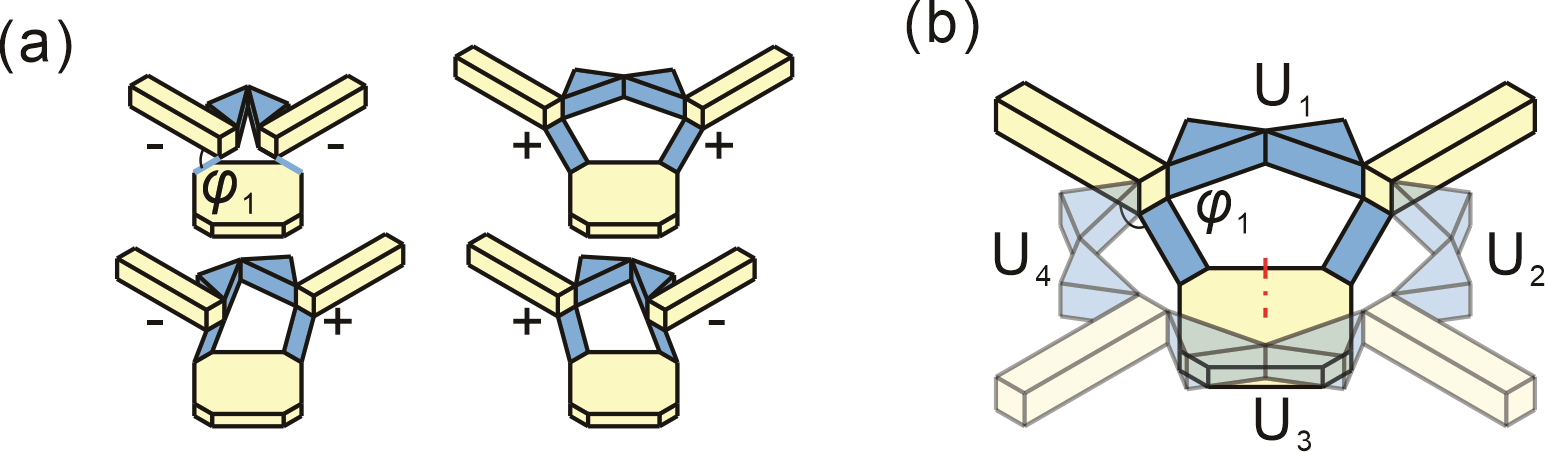
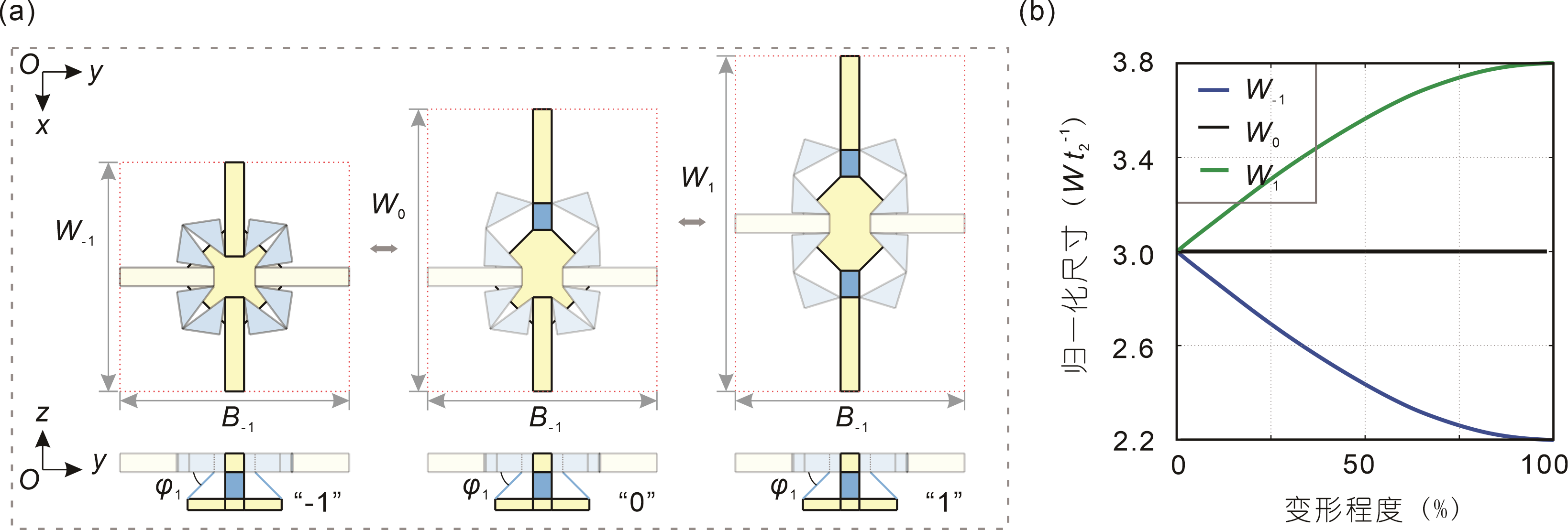
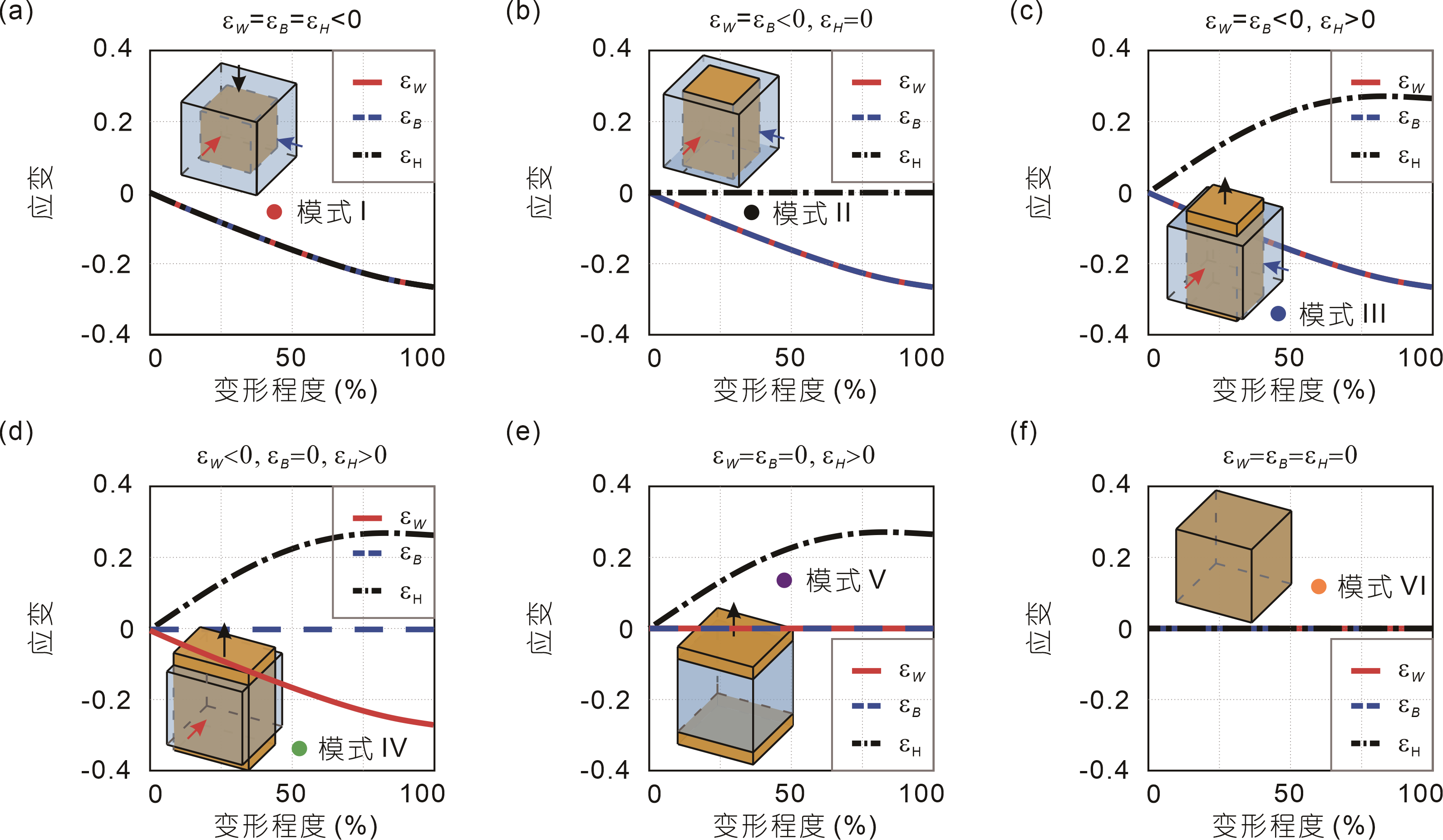
The pursuit of programmable matter is reshaping materials science. Mechanical metamaterials, deriving properties from architecture rather than composition, have unlocked unconventional capabilities like negative compressibility. Among these, Poisson’s ratio is critical for deformation mechanics and energy absorption. While researchers have engineered metamaterials with fixed Poisson’s ratios using re-entrant lattices or origami, achieving sign-switchable Poisson’s ratios within a single structure remains a challenge. Existing solutions are mostly limited to two-dimensional systems or suffer from coupled orthogonal kinematics. Consequently, a truly three-dimensional system capable of continuously spanning the full spectrum of Poisson’s ratio—covering all deformation modes across principal directions—has yet to be realized.

        Recently, the team of Professor Yan Chen of Tianjin University developed a novel class of reconfigurable modular origami metamaterial based on orthogonally decoupled kinematics. Through a digital strain-state encoding strategy, the team successfully realized a full spectrum of Poisson’s ratio responses within a single structural system. The study, titled “Reconfigurable modular origami metamaterial with full-spectrum programmable Poisson’s ratio” was invitedly published online on December 18, 2025, in SCIENTIA SINICA Physica, Mechanica & Astronomica.

        The design is inspired by a spatial linkage mechanism with motion bifurcation. The researchers mapped this mechanism's parameters onto origami components—rectangular panels, triangular panels, and an octagonal prismatic base—giving the unit a single degree of freedom (DOF). As shown in Fig. 1, the unit features multiple motion branches. It can evolve along path M1 to achieve symmetric contraction (-, -) or expansion (+, +), or along path M2 to exhibit antisymmetric mixed states (-, +) and (+, -), demonstrating rich bifurcation characteristics.

Figure 1. A 2D module assembled from four identical basic units around a central vertical axis.

        To extend this reconfigurability, four identical units are assembled into a closed 2D module (Fig. 1). Due to the system's four-fold rotational symmetry, the deformation is orthogonally decoupled. As illustrated in Fig. 2, each direction exhibits three distinct states. When both rectangular panels move toward the octagonal prismatic base, the width W_-1 monotonically decreases with increasing deformation degree, corresponding to a contracting response. When one panel moves toward and the other away from the base, the opposing motions balance each other, maintaining a constant dimension W₀ in that direction. Conversely, when both panels move away from the base, W₁ increases continuously, producing an expanding behavior. To formalize these three deformation behaviors, a digital strain-state encoding scheme is introduced, in which the macroscopic response along each direction is represented by a discrete variable S_x∈{-1, 0, +1}, corresponding respectively to contraction (-1), zero strain (0), and expansion (+1). The same encoding applies independently along the y-axis (breadth B), yielding S_y∈{-1, 0, +1}. Because the motions of the two orthogonal pairs of panels are kinematically decoupled, the overall in-plane deformation state of the module can be expressed as the C_{(Sx, Sy)}.

Figure 2. Orthogonally decoupled deformation states of the 2D module.

        Based on this digital encoding strategy, the configuration space of the 2D module is summarized into four representative deformation modes, as shown in Fig. 3.

Figure 3. Four representative deformation modes of the 2D module.

        Mode I corresponds to the continuous deformation from the bifurcation configuration ⑨ to either the fully contracted configuration ① or the fully expanded configuration ⑤. In this mode, strains along both principal axes share the same sign and magnitude, as shown in Fig. 4(a) and 4(b). This results in a constant Poisson’s ratio of −1, exhibiting typical auxetic (negative Poisson’s ratio) behavior. In Mode II, the module transitions from configuration ⑨ to ② or ⑥. Deformation occurs solely along one principal direction while the orthogonal dimension remains unchanged. As illustrated in Fig. 4(c) and 4(d), this mode corresponds to a zero Poisson’s ratio response. Mode III occurs during the transition from configuration ⑨ to ③ or ⑦. Here, the strains along the two principal directions have opposite signs—one contracts while the other expands. The strain curves in Fig. 4(e) and 4(f) indicate that this mode corresponds to a positive Poisson’s ratio behavior, characteristic of conventional materials. In contrast, Mode IV corresponds to the transformation from configuration ⑨ to ④ or ⑧. In this mode, strains in both principal directions are zero, as shown in Fig. 4(g) and 4(h). The overall dimensions of the module remain constant; internal components merely undergo geometric rearrangement without introducing macroscopic deformation. This mode-dependent deformation behavior demonstrates that the Poisson’s ratio in a single 2D module can be deterministically programmed through purely geometric reconfiguration, thereby spanning the full spectrum of Poisson’s ratio, including negative, zero, and positive values.

Figure 4. Strain responses of the 2D module under four representative deformation modes.

         By connecting six 2D modules using L-shaped linkages, the study further constructed a 3D cubic metamaterial (Fig. 5). Theoretical analysis indicates that this structure possesses 27 kinematically compatible configurations, which can be summarized into six representative deformation modes (Fig. 6). These modes correspond to C_{(-1, -1, -1)}, C_{(-1, -1, 0)}, C_{(-1, -1, 1)}, C_{(-1, 0, 1)}, C_{(0, 0, 1)}, and C_{(0, 0, 0)}, respectively. Each mode represents a specific combination of encoded states along the three principal directions, thereby enabling programmable control over global deformation behaviors.

Figure 5. Schematic illustration of the 3D cubic metamaterial construction.

Figure 6. Configuration space of the cubic metamaterial and its six representative deformation modes.

         As shown in Fig. 7(a), in Mode I, the C_{(-1, -1, -1)} configuration metamaterial contracts uniformly in all three principal directions, exhibiting a perfectly isotropic negative Poisson’s ratio. Mode II corresponds to the C_{(-1, -1, 0)} configuration in Fig. 7(b). Here, the metamaterial maintains a negative Poisson’s ratio in the xoyplane, while deformation in the z-direction is zero, presenting a zero Poisson’s ratio characteristic. In Mode III, shown in Fig. 7(c), the C_{(-1, -1, 1)} configuration retains a negative in-plane Poisson’s ratio while exhibiting conventional positive Poisson’s ratio behavior out-of-plane. In Mode IV (Fig. 7(d)), the C_{(-1, 0, 1)} configuration displays strain signs of negative, zero, and positive along the three principal directions, respectively, demonstrating high anisotropy. In Mode V (Fig. 7(e)), the C_{(0, 0, 1)}configuration realizes purely one-dimensional deformation, where strain occurs exclusively along the z-axis, effectively forming a programmable uniaxial material. Finally, Mode VI in Fig. 7(f) embodies the complete decoupling of internal kinematics and macroscopic deformation; the metamaterial achieves pure internal reconfiguration while all global dimensions remain constant. Collectively, these six modes cover the full spectrum of Poisson’s ratio responses, ranging from perfectly isotropic to highly anisotropic behaviors.

Figure 7. Strain responses of the cubic metamaterial under six representative deformation modes.

         Beyond programmable mechanical properties, the researchers successfully converted ambient thermal energy into driving force by integrating bimetallic actuation hinges at key connections, leveraging the differential thermal expansion of metals. Experiments demonstrated (Fig. 8) that as the temperature increased from 20°C to 140°C, the metamaterial could exhibit either positive thermal expansion (expanding upon heating) or negative thermal expansion (contracting upon heating) according to a preset "program."

Figure 8. Thermal response of the 2D module integrated with bimetallic actuation hinges.

        In summary, this study proposes a class of reconfigurable modular origami metamaterials with orthogonally decoupled kinematics, achieving programmable control over Poisson’s ratio and covering the theoretically full spectrum of Poisson's ratio responses. Utilizing a bifurcation-based reconfigurable mechanism as a geometric engine, the research establishes a physical mapping between geometric configurations and mechanical responses—as well as thermal properties. This work provides a novel perspective for the development of programmable thermo-mechanical metamaterials and demonstrates broad application potential in fields such as aerospace morphing structures and soft robotics.

Weiqi Liu, Jiayao Ma, Yan Chen*. Reconfigurable modular origami metamaterial with full-spectrum programmable Poisson’s ratio, SCIENTIA SINICA Physica, Mechanica & Astronomica. (https://doi.org/10.1360/SSPMA-2025-0510)